5. Fall mit Luftwiderstand

5.1 Theorie

Bei fallenden Körpern mit größerem Querschnitt ist der Luftwiderstand nicht mehr zu vernachlässigen. Im Gegensatz zum freien Fall wirken hier zwei Kräfte auf den Körper: seine Gewichtskraft F_G und die Luftwiderstandskraft F_L.

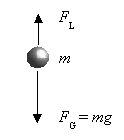
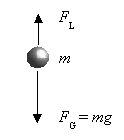
Unter der Wirkung der Gewichtskraft wächst die Geschwindigkeit v des Körpers. Mit der Geschwindigkeit v nimmt aber auch der Luftwiderstand F_L zu, der der beschleunigenden Kraft entgegengerichtet ist. Die resultierende Kraft aus beiden ist somit:

Wenn die Geschwindigkeit groß genug ist, ist die Luftwiderstandskraft genau so groß wie die Gewichtskraft des Körpers. Die resultierende Kraft ist dann Null:

d.h. der Körper bewegt sich kräftefrei, also gleichförmig mit konstanter Geschwindigkeit.

5.2 Versuch

Aufbau:

Es werden Papiertrichter aus Kopierpapier (mit 80 g/m²) gebaut.
Daten:
Kreis mit Radius r = 10,0 cm; daraus
Kreisektor mit Mittelpunktswinkel j = 325° ausschneiden.
Zum Zusammenkleben wird ein Kreissektor mit 5° Überlappung gewählt.

Aus einer Höhe von 2,5 m wird ein solcher Trichter fallen gelassen und die Fallzeit für den letzten Meter der Fallstrecke gemessen. Es wird angenommen, dass der Trichter diese Strecke mit der konstanten Endgeschwindigkeit durchfällt. Diese Geschwindigkeit ergibt sich also aus

Der Versuch wird danach mit vier gleichen ineinandergesteckten Trichtern wiederholt.

Messwerte:

1 Trichter: t = 0,90 s (Mittelwert aus 8 Einzelmessungen)

4 Trichter: t = 0,45 s (Mittelwert aus 8 Einzelmessungen)

Damit ergeben sich die Mittelwerte für die Geschwindigkeiten:

Auswertung:

Im Kräftegleichgewicht gilt für einen Trichter

Werden vier Trichter ineinander gesteckt, vervierfacht sich die Masse, die Gewichtskraft und die Luftwiderstandskraft:

Wenn die Luftwiderstandskraft proportional zur Geschwindigkeit v wäre, dann müsste sich die Endgeschwindigkeit bei vierfacher Masse auch vervierfachen. Tatsächlich ist aber beobachtet worden, dass sich die Endgeschwindigkeit nur verdoppelt hat. Daraus ist der Schluss zu ziehen, dass F_L proportional zum Quadrat der Geschwindigkeit sein muss:

denn dann gilt:

Der Luftwiderstand F_L hängt außer vom Quadrat der Geschwindigkeit noch von folgenden Größen ab:

der Fläche A, die der Körper der Luft bietet,
der Luftdichte r
der Geometrie des Körpers, die im sogenannten Widerstandsbeiwert c_W erfasst wird.

Damit gilt:

Für die im Versuch verwendeten Trichter ist A = 0,0249 m², c_W zwischen 1,00 und 1,08.

Die Luftdichte beträgt unter Normalbedingungen an der Erdoberfläche.

Mit diesen Daten und den gemessenen Geschwindigkeiten ergibt sich:

Dies bestätigt den Zusammenhang .

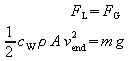
5.3 Berechnung der theoretischen Endgeschwindigkeit

Die Beziehung für das Kräftegleichgewicht

wird nach der Geschwindigkeit aufgelöst:

Die Masse eines der im Versuch verwendeten Papiertrichter beträgt m = 2,35 g. Mit den angegebenen Grenzen von c_W ergibt sich:

1 Trichter: v_end,1 = 1,150 ... 1,195 m/s ; Mittelwert: 1,17 m/s

4 Trichter: v_end,4 = 2,350 ... 2,300 m/s ; Mittelwert: 2,35 m/s.

Im Rahmen der Messgenauigkeit stimmen diese theoretischen Werte mit den gemessenen Fallgeschwindigkeiten überein.

typische Widerstandsbeiwerte c_W:
Fallschirm	1,4
dünne, ebene Platte, senkrecht zur Strömung	1,11
LKW	0,8
Mensch, stehend	0,78
Motorrad, unverkleidet	0,7
Kugel	0,45
PW Smart	0,37
PKW A2	0,25
optimal gestaltetes Flugzeug	0,15
Tropfenform	0,05

5.4 Computersimulation des Falls mit Luftwiderstand

Die Berechnung der Zeitverläufe von Ort und Geschwindigkeit beim Fall eines Körpers unter Berücksichtigung des Luftwiderstands ist deswegen schwierig, weil die Beschleunigung nicht konstant ist. Sie verändert sich ja in jedem Moment der Bewegung, da sich die Geschwindigkeit verändert:

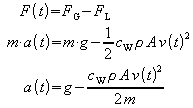
Zur Berechnung der Bewegung kann aber ein Rechenmodell verwendet werden, das auf einem Computer eingesetzt werden kann.

Bei dem sogenannten einfachen Euler-Verfahren wird davon ausgegangen, dass zu einem bestimmten Start-Zeitpunkt t die Startwerte der Geschwindigkeit v(t), des Ortes s(t) und der Beschleunigung a(t) bekannt sind. Es sollen dann näherungsweise die nächsten Funktionswerte für den Zeitpunkt berechnet werden.

Aus der Definition der Beschleunigung

folgt eine Näherung für die Geschwindigkeit nach dem Zeitschritt:

Dies wird um so besser mit dem genauen Wert der Geschwindigkeit im nächsten Zeitpunkt übereinstimmen, je kleiner der Zeitschritt gewählt wird.

Entsprechend ergibt sich aus der Definition der Geschwindigkeit

die Näherungsbeziehung

Für den nächsten Rechenschritt ist dann der Zeitpunkt der Start-Zeitpunkt und die gerade berechneten Werte von v und s sind die neuen Startwerte. Außerdem muss noch die Beschleunigung zu dem neuen Start-Zeitpunkt berechnet werden.

Schema:

Für einen der verwendeten Trichter liefert die Rechnung folgende Verläufe von Fallgeschwindigkeit v und Fallstrecke s in Abhängigkeit von der Zeit t:

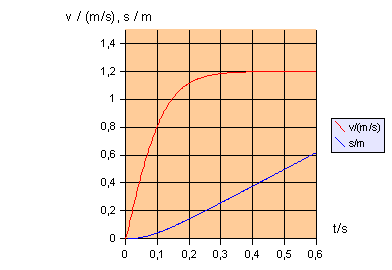
Daraus ist abzulesen, dass die Endgeschwindigkeit nach etwa 0,4 s erreicht wird. In dieser Zeit hat der Trichter eine Strecke von etwa 0,38 m durchfallen. Der Trichter wurde im Versuch aus der Höhe 2,5 m fallen gelassen. Die Annahme, dass er auf dem letzten Meter der Fallstrecke mit konstanter Geschwindigkeit fällt, war also gerechtfertigt.

Die folgende Excel-Datei führt die Simulation durch. Wenn Sie auf Ihrem Computer Excel installiert haben, können Sie diese Datei speichern und ausführen oder auch online ausführen. Klicken Sie dazu auf den folgenden Screenshot.

Übungen

1. Der Raketenmotor eines Raumfahrzeugs wirbelt beim Landen auf dem Mond sehr viel Staub auf. Warum ist nach dem Abstellen des Motors die Sicht sofort wieder klar – im Gegensatz zur Landung auf der staubigen Erdoberfläche?

2. Rechnen Sie nach: Ein halbkugelig geformter Fallschirm (c_W-Wert 1,35) mit 2 m Radius sorgt in Luft () bei einer Last von 50 kg für die Sinkgeschwindigkeit 6,8 m/s.

3. Ein PKW (c_W = 0,35) mit der Querschnittsfläche 2,0 m² fährt gleichförmig mit 30 m/s. Wie groß ist die Luftwiderstandskraft ()? Bei Gegenwind mit der Windgeschwindigkeit 10 m/s erhöht sich die Strömungsgeschwindigkeit auf 40 m/s. Wie groß ist jetzt die Luftwiderstandskraft?

Lösung: F_L = 393,75 N (bzw. 700 N)