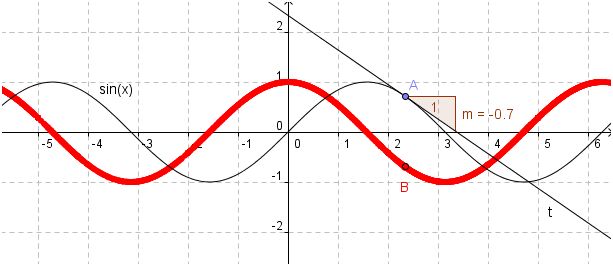
Die folgende Abbildung zeigt den Graphen der Sinusfunktion und stellt die Steigung der Tangenten an den Graphen dar (rot).
Die Zusammenhänge können Sie mit folgendem interaktiven Java-Applet
genauer untersuchen: [Ableitung der Sinusfunktion].
Der
Verlauf der Tangentensteigungen lässt vermuten, dass die
Ableitung der Sinusfunktion die Kosinusfunktion sein könnte.
Zur
genaueren Untersuchung wird die Ableitung von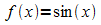 
gemäß der Definition des Begriffes Ableitung an einer
Stelle x0 als Grenzwert des Differenzenquotienten
bestimmt. Der Differenzenquotient lautet:
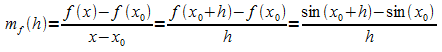
Durch Anwenden des Additionstheorems
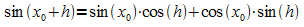
kann er wie folgt umgeformt werden:
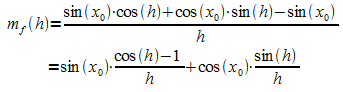
Um
den Grenzwert für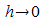 
bilden zu können, müssen die Grenzwerte
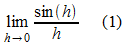
und
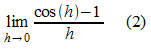
bestimmt werden.
|
Der Anschauung am Einheitskreis ist zu entnehmen: Für kleine Werte von x nähern sich sin(x) und x immer weiter an. Das bedeutet:
|
|
Der cos-Term in mf (h) lässt sich so umformen:
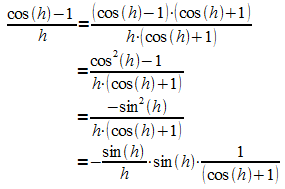
Daraus folgt:
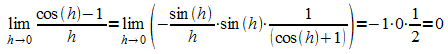(2)
Mit den Grenzwerten (1) und (2) erhält man nun den Grenzwert des Differenzenquotienten der Sinusfunktion an einer Stelle x0:
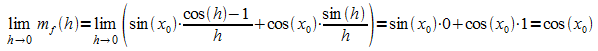
Diese
Betrachtungen gelten für alle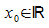 
.
Somit ergibt sich:
Die Ableitungsfunktion der Sinusfunktion ist die Kosinusfunktion:
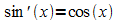
Entsprechend kann gezeigt werden:
Die Ableitungsfunktion der Kosinusfunktion ist die negative Sinusfunktion:
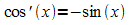
Betrachtet man die höheren Ableitungen, so ergeben sich folgende Zusammenhänge:
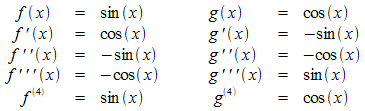
Der Differenzenquotient der Tangensfunktion wird in folgender Form geschrieben:
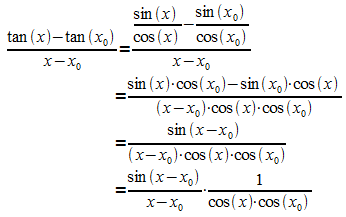
Daraus ergibt sich unter Verwendung des obigen Grenzwertes (1)
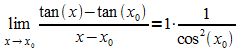
Also:
Die
Tangensfunktion ist differenzierbar in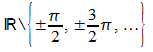 
,
und
es gilt:
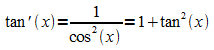für alle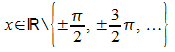 
Übungen
1. Führen
Sie die Herleitung von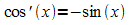
entsprechend zur Herleitung von
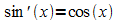durch.
2. Begründen Sie:
a) Nullstellen der Sinusfunktion sind Extremstellen der Kosinusfunktion,
b) Nullstellen der Kosinusfunktion sind Extremstellen der Sinusfunktion.
3. Bestimmen Sie die Wendestellen der Sinus- und der Kosinusfunktion.
4. Begründen
Sie: Die Sinus- und die Kosinusfunktion sind Lösungen der
Differentialgleichung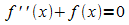 
.
(1)