8. Kreisbewegung

Bisher wurden nur geradlinige Bewegungen betrachtet. Als einfachstes Beispiel für eine nicht-lineare Bewegung soll nun die Bewegung eines Körpers auf einer Kreisbahn untersucht werden.

1. Wenn sich der Betrag der Geschwindigkeit auf der Kreisbahn nicht ändert, spricht man von einer gleichförmigen Kreisbewegung.

Durch welche Größen wird eine gleichförmige Kreisbewegung zweckmäßig beschrieben? Bei der gleichförmigen linearen Bewegung wurden folgende Größen verwendet:

Bei einer Kreisbewegung wählt man entsprechend die folgenden Größen:
 
  • den überstrichenen Winkel ,
  • die dazu benötigte Zeit t und – da und t proportional sind –
  • die Winkelgeschwindigkeit .

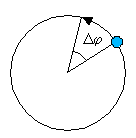Mathematischer Einschub: Das Bogenmaß eines Winkels

Zum Vollwinkel 360° gehört bei einem Kreis der Umfang. Zu kleineren Winkeln gehört entsprechend nur ein Teil des Kreisumfanges. Ein solcher Teil wird als Kreisbogen b bezeichnet.

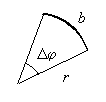
Für die Bogenlänge findet man:
 

b
360°
180°
90°

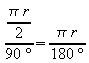Es ist also

.

Umgeformt:

.

Die rechte Seite ist unabhängig vom Kreisradius und nur durch den Winkel bestimmt. Dieser Term wird als das Bogenmaß des Winkels bezeichnet:

.

Der Index „rad“ steht für die Einheit des Bogenmaßes: 1 Radiant (rad). Die Einheit wird bei der Angabe eines Winkels im Bogenmaß jedoch meistens weggelassen.

Wird der Winkel im Bogenmaß angegeben, so ergibt sich für die Bogenlänge eines Kreisbogens mit Radius r die Beziehung

.

2. Die Zeit, die für einen vollständigen Durchlauf der Kreisbahn benötigt wird, wird mit T bezeichnet. In dieser Zeit wird der Winkel (im Bogenmaß)  überstrichen. Damit ergibt sich für die Winkelgeschwindigkeit bei der gleichförmigen Kreisbewegung

.

Unter der Drehfrequenz versteht man den Quotienten aus Anzahl n von Umdrehungen und der dazu benötigten Zeit:

.

Da ist, folgt

.

Unter Verwendung der Drehfrequenz lautet die Winkelgeschwindigkeit

.

3. Wird die Winkelgeschwindigkeit mit dem Kreisradius r multipliziert, so ergibt sich

,

also das Verhältnis von Kreisumfang und Zeit, die zum Durchlaufen des Kreisumfanges benötigt wird. Das Produkt aus Winkelgeschwindigkeit und Kreisradius wird daher als Bahngeschwindigkeit bezeichnet:

.

4. Die Bewegung eines Körpers auf einer Kreisbahn ist in jedem Zeitpunkt tangential zum Kreisbogen gerichtet. Der Vektor der Bahngeschwindigkeit ändert also laufend seine Richtung. Dazu ist aber eine Kraft erforderlich, die ständig zum Kreismittelpunkt gerichtet ist – die sogenannte Zentripetalkraft FZ.

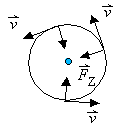
Das wiederum bedeutet, dass die gleichförmige Kreisbewegung eine beschleunigte Bewegung ist. Die Zentripetalbeschleunigung bestimmte Newton mit folgender Überlegung.

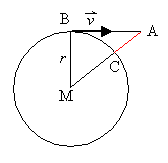
Ohne Zentripetalkraft würde der Körper in der Zeit  die Strecke  zurücklegen. Damit er aber – ausgehend von B – wieder auf der Kreisbahn bei C ankommt, muss er gleichzeitig in dieser Zeit unter Wirkung der Zentripetalkraft von A nach C bewegt werden:

.

Im Dreieck MAB liest man ab:

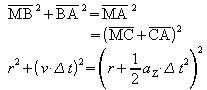
Ausquadriert:

Subtraktion von r2 und Division durch  ergibt

.

Die reale Bewegung auf der Kreisbahn stimmt um so besser mit der hier betrachteten Zerlegung in zwei Bewegungsabschnitte überein, je kleiner  ist. Im Grenzfall  folgt

,

und damit:

.

5. Bei geradlinigen Bewegungen wurde die Grundgleichung der Mechanik in der Form F = ma gefunden. Darf diese Gleichung auch bei der Kreisbewegung verwendet werden? Darüber gibt folgender Versuch Auskunft.
 

 

Ein Wagen der Masse m = 49 g kann sich auf einer Schiene bewegen. Über eine Umlenkrolle ist er an einem aufgehängten Kraftmesser befestigt. Die Schiene ist auf einem Motor M angebracht und kann in Kreisbewegung mit der Umlaufdauer T versetzt werden. Gemessen werden FZ, r und T.

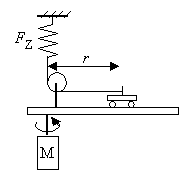Wenn die Grundgleichung auch hier angewendet werden darf, dann gilt

.

Dieser theoretische Wert der Zentripetalkraft ist mit den gemessenen Werten zu vergleichen.

Messungen:

Die Umlaufdauer wird aus 10 Umläufen bestimmt.

Im Rahmen der Messgenauigkeit stimmen die über  berechneten Werte mit den gemessenen Werten überein. Die Grundgleichung  gilt also auch bei der Kreisbewegung.

6. Die Zentripetalkraft wird oft mit der Zentrifugalkraft verwechselt. Zwischen diesen beiden Kräften muss aber unterschieden werden, wie die folgende Betrachtung zeigen soll.

Eine Drehbewegung kann aus verschiedenen Bezugssystemen betrachtet werden, z.B.

Denken Sie zur Veranschaulichung an ein Karussell: Wenn Sie daneben stehen und der Drehung zusehen, befinden Sie sich in einem „Laborsystem“ und beschreiben die Drehung aller auf dem Karussell befindlichen Gegenstände als eine Kreisbewegung. Sitzen Sie dagegen selbst auf dem Karussell, bewegt sich für Sie nichts auf dem Karussell im Kreis, da Sie natürlich ein Bezugssystem verwenden, das mit dem Karussell verbunden ist – eben ein mitrotierendes Bezugssystem.

Das Karussell lässt sich durch folgende vereinfachte Anordnung beschreiben: Eine Kreisscheibe rotiert mit konstanter Winkelgeschwindigkeit um eine Drehachse im Mittelpunkt der Scheibe. Am Rand der Scheibe befindet sich eine Kugel, die über eine Feder mit der Achse verbunden ist.
 

 

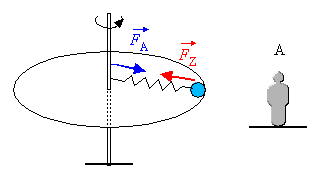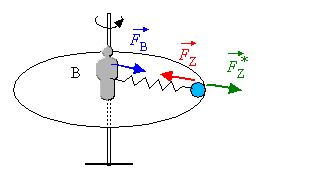A ist ein ruhender Beobachter im Laborsystem. Er stellt fest, dass auf die Kugel eine Zentripetalkraft  wirkt und die Kugel sich daher auf einer Kreisbahn bewegt.
B ist ein mitrotierender Beobachter auf der rotierenden Scheibe. Er stellt fest, dass auf die Kugel eine Kraft  wirkt. Dennoch bleibt die Kugel – im mitrotierenden Bezugssystem – in Ruhe. Also folgert der Beobachter B, dass es zu  eine Gleichgewichtskraft  gibt, deren Betrag gleich dem Betrag von  ist und die nach außen weist. Dies ist die Zentrifugalkraft (auch Fliehkraft genannt).

Diese Kraft weist im Vergleich zu den anderen auftretenden Kräften eine Besonderheit auf.

Nach dem 3. Newton'schen Axiom (Wechselwirkungsprinzip) tritt zu jeder Kraft auch eine Gegenkraft (Wechselwirkungskraft) auf.

Beobachter A stellt fest: Die Gegenkraft zur Zentripetalkraft  ist die Kraft , die an der Drehachse angreift.

Beobachter B stellt fest: Die Gegenkraft zur Kraft  ist die Kraft , die an ihm angreift, wenn er die Feder festhält. Eine Gegenkraft zu  findet er dagegen nicht. Die Zentrifugalkraft ist nicht Teil eines Wechselwirkungs-Kräftepaares.

Solche Kräfte wie die Zentrifugalkraft nennt man Scheinkräfte (oder Trägheitskräfte). Scheinkräfte sind daran zu erkennen, dass sie keine Gegenkräfte besitzen. Sie treten nur in beschleunigten Bezugssystemen auf.

Als zweites Beispiel wird ein Kegelpendel betrachtet: An einem vertikal aufgestellten Stab wird ein Fadenpendel befestigt und der Stab in Drehung versetzt. Der Pendelkörper führt nach dem Ende des Beschleunigungsvorgangs eine horizontale Kreisbewegung aus. Ein Beobachter A im Laborsystem beschreibt die Situation wie folgt:
 
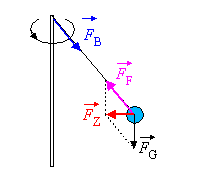Der Faden übt eine Zugkraft  auf den Pendelkörper aus; als Wechselwirkungskraft tritt am Stab die Kraft  auf.

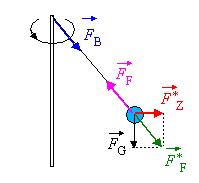Die für die Kreisbewegung nötige Zentripetalkraft ergibt sich aus der vektoriellen Addition von Zugkraft  und Gewichtskraft  des Pendelkörpers.
Ein mitrotierender Beobachter B stellt fest:
Auf den Pendelkörper wird die Kraft  ausgeübt (Wechselwirkungskraft dazu ist ).

Trotzdem bleibt der Pendelkörper – im mitrotierenden Bezugssystem – in Ruhe. Es muss also eine Gleichgewichtskraft  geben. Zu dieser Kraft gibt es keine Gegenkraft.

lässt sich in zwei Komponenten zerlegen:

Die Beschreibung durch den Beobachter B ist natürlich gleichwertig zu der Beschreibung des Beobachters A:

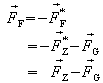
also:

.

7. Ein weiteres Beispiel für eine Scheinkraft in rotierenden Bezugssystemen ist die Coriolis-Kraft. Sie wurde nach ihrem Entdecker Gaspard Gustave de Coriolis (1792-1843) benannt. Auf einen Körper, der sich in einem rotierenden Bezugssystem bewegt, wirkt sie senkrecht zur Bewegungsrichtung des Körpers und senkrecht zur Rotationsachse des Systems. Ihr Auftreten wird durch die Trägheit der sich bewegenden Massen verursacht.

Ein Experiment zum Nachweis der Corioliskraft zeigt die folgende Abbildung.

Der dargestellte Versuchsaufbau besteht aus einer drehbar gelagerten Scheibe und einer in Richtung Scheibenmittelpunkt leicht geneigten Rinne. Wird eine Stahlkugel auf die Rinne gelegt, so rollt sie diese hinab und überquert die Scheibe.

Für einen außerhalb des Systems stehenden Beobachter im Laborsystem ist es dabei gleich, ob die Scheibe rotiert oder nicht. Er beobachtet in beiden Fällen, dass die Kugel beim Überqueren der Platte die gleiche geradlinige Bewegung vollzieht.

Anders stellt sich die Situation für einen Beobachter dar, der sich auf der Scheibe befindet. Während er bei ruhender Scheibe ebenfalls eine geradlinige Bewegung der Kugel beim Überqueren der Scheibe wahrnimmt, bemerkt er, dass die Kugel beim Überqueren der rotierenden Scheibe in Abhängigkeit von der Winkelgeschwindigkeit des Systems entgegen der Drehrichtung abgelenkt wird. Man kann diese Ablenkung sehr gut zeigen, indem man, wie in der Abbildung dargestellt, eine Kugel über eine berußte Platte rollen läßt.

Die Ursache für den beobachteten Effekt liegt in der Trägheit der Kugelmasse. Die Stahlkugel wird beim Herabrollen der Rinne beschleunigt. Mit der am Ende der Rinne erreichten Endgeschwindigkeit bewegt sie sich dann in in geradlinig gleichförmiger Bewegung über die Scheibe. Entsprechend des Trägheitsgesetzes behält sie diese Zustand bei, solabge keine äußere Kraft auf sie einwirkt. Im ruhenden Laborsystem wirkt auf die Kugel mit Ausnahme der Gravitation (und der zu vernachlässigenden Rollreibungskraft) keine Kraft. Überquert die Kugel jedoch die rotierende Scheibe, so dreht sich das rotierende Bezugssystem, das ein Beobachter auf der Scheibenoberfläche verwendet, unter der Kugel hindurch. Dadurch bewegt sich die Kugel für einen Beobachter im rotierenden Bezugssystem auf einer scheinbar gekrümmten Bahn.

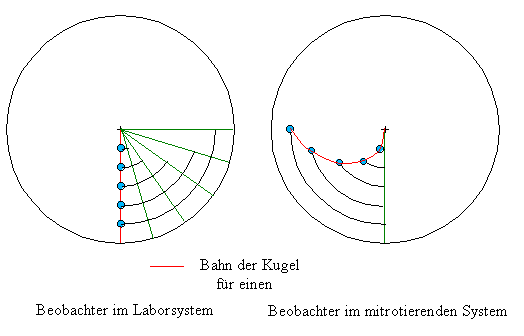
Will der Beobachter im rotierenden Bezugssystem nun die Kugel auf eine für ihn geradlinig erscheinende Bahn bringen, muss er dazu eine Kraft aufwenden, deren Betrag dem der Corioliskraft entspricht.

Übungen

(Die Seitenangaben beziehen sich auf den Teilband für Klasse 11. Im Gesamtband sind die Seitennummern um 2 höher.)
 
empfohlene Aufgaben aus dem Lehrbuch Lösungen
S.99, A3 v = 31,4 m/s

aZ = 7896 m/s2

F = 7,9 N 
S.99, A4 v = 47,4 m/s

f = 0,50 s–1
S.99, A5 f = 5,03 s–1
S.99, A6 a) FZ = 2,53 N

c) kleiner

d) FZ = 1,62 N
S.99, A7  

Weitere Übungen

1. Ein Düsenflugzeug fliegt mit 2 000 km/h eine horizontal liegende, kreisförmige Bahn.

a) Wie groß ist die Zentripetalbeschleunigung bei r = 10,0 km?

b) Ein Mensch erträgt (für die Dauer von 10 s) eine Beschleunigung vom Betrage 6g (g: Fallbeschleunigung). Wie groß muss der Radius der Bahn mindestens sein, damit aZ < 6g?

2. Ein Elektromotor macht in 1 Minute 3600 Umdrehungen. Mit welcher Frequenz dreht er sich? Mit welcher Geschwindigkeit dreht sich ein Punkt des Rotors, der sich in 10 cm Abstand von der Drehachse befindet?

3. Die Antriebswelle für das Band eines Cassettenrekorders (Wiedergabegerät aus der Steinzeit der Unterhaltungselektronik;-) ) hat einen Durchmesser von 2 cm. Mit welcher Frequenz muss sich der Motor drehen, wenn das Band mit einer Geschwindigkeit von 4,75 cm/s abgespielt wird?

4. Ein Satellit bewegt sich auf einer Kreisbahn von Ost nach West in 200 km Höhe über dem Äquator um die Erde.

Erdumfang am Äquator: 40 076,6 km

Fallbeschleunigung in 200 km Höhe: g = 9,22 m/s2

Umlaufzeit der Erde bezogen auf den Sternenhimmel:
T = 1 Sterntag = 23 h 56 min 4 s = 86 164 s

a) Wie groß ist der Bahnradius des Satelliten?

b) Welche Winkelgeschwindigkeit und Umlaufzeit (bezogen auf die Erde) ergibt sich für den Satelliten, wenn man die Eigendrehung der Erde unberücksichtigt lässt?

c) Welche Winkelgeschwindigkeit und Umlaufzeit (bezogen auf die Erde) ergibt sich für den Satelliten, wenn man die Eigendrehung der Erde mitberücksichtigt?


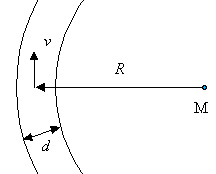
5. Ein LKW hat die Spurweite d = 1,8 m, seine Räder haben den Durchmesser 2r = 80 cm. Das Fahrzeug durchfährt eine kreisförmige Kurve, der Radius des Kreisbogens beträgt R = 60 m. Der Fahrzeugmittelpunkt hat die Geschwindigkeit v = 54 km/h.

a) Man kann die Fahrzeugbewegung als eine Drehbewegung um die vertikale Achse auffassen, die durch den Krümmungsmittelpunkt der Kurve geht. Welche Winkelgeschwindigkeit  hat das Fahrzeug bezüglich dieser Drehbewegung?

b) Die Räder des Fahrzeugs beschreiben eine Drehbewegung um die Radachsen. Welche Winkelgeschwindigkeiten  und  haben die Wagenräder bezüglich dieser Bewegung?
 
 
 

Lösungen

1. a) aZ = 30,83 m/s2

b) r > 5,24 km

2. f = 60s–1 ; v = 37,7 m/s

3. f = 0,76 s–1

4. a) r = 6578 km

b) 

c) 

5. a)

b)