2. Beschleunigte Bewegung

Gleichförmige Bewegungen treten selten auf. So vergrößert ein Auto etwa beim Anfahren seine Geschwindigkeit; beim Abbremsen wird die Geschwindigkeit verringert. In Kurven ist die Bewegung nicht geradlinig und schon deshalb nicht gleichförmig. Allgemein sagt man:

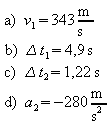
Ein Körper, dessen Geschwindigkeit sich ändert, führt eine beschleunigte Bewegung aus. Eine Geschwindigkeitsänderung kann in einer Änderung des Betrages der Geschwindigkeit, einer Änderung der Richtung der Bewegung oder in einer Änderung beider Größen bestehen.

Zunächst soll die geradlinig beschleunigte Bewegung betrachtet werden, bei der sich nur der Betrag der Geschwindigkeit ändert.

2.1 Zeit-Weg-Funktion

Versuch:

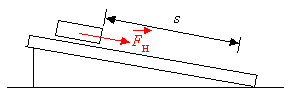
Eine Luftkissenfahrbahn wird leicht geneigt. Die Hangabtriebskraft wirkt dann als beschleunigende Kraft auf den Gleiter. Gemessen wird die Zeit, die der Gleiter benötigt, um verschieden lange Strecken zurückzulegen.

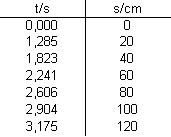
Messwerte:

Eingestellt wurde jeweils die Strecke s. Die Zeitmessung erfolgte mit einem elektronischen Zähler, der mit Lichtschrankensignalen gestartet und gestoppt wurde. In der Tabelle sind zu jeder Strecke s die Mittelwerte aus 3 Einzelmessungen der Zeit t eingetragen.

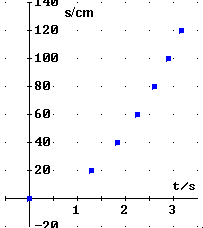
Auswertung:

Ein proportionaler Zusammenhang von t und s ist auf den ersten Blick auszuschließen.

Die graphische Darstellung der Messwerte lässt vermuten, dass ein quadratischer Zusammenhang vorliegen könnte: .

Die rechnerische Überprüfung zeigt, dass der Quotient s/t2 als konstant betrachtet werden kann:

Als Mittelwert ergibt sich:

.

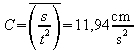Die Zeit-Ort-Gleichung der Bewegung lautet also

.

Der Graph passt sich den Messwerten gut an:

2.2 Geschwindigkeit bei beschleunigter Bewegung

Bei einer beschleunigten Bewegung werden nicht – wie bei der gleichförmigen Bewegung – in gleichen Zeiten gleiche Strecken zurückgelegt. Die Größe Geschwindigkeit kann daher nicht als Quotient von Strecke und Zeit definiert werden. Dieser Quotient hat hier die Bedeutung einer Durchschnittsgeschwindigkeit (auch Intervallgeschwindigkeit genannt):
 

Je kleiner aber das Zeitintervall  gewählt wird, umso besser stimmt diese Durchschnittsgeschwindigkeit mit der Geschwindigkeit in einem beliebigen Zeitpunkt dieses Zeitintervalls überein.

Messung:

Um aus den obigen Messdaten die Geschwindigkeit näherungsweise zu bestimmen, wird wie folgt vorgegangen:

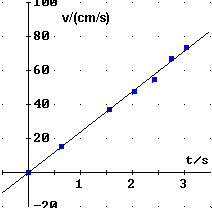
Zu vermuten ist ein proportionaler Zusammenhang. Der Mittelwert aus den Quotienten von  ist

.

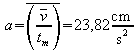Die Zeit-Geschwindigkeit-Gleichung der untersuchten beschleunigten Bewegung lautet also:

.

Der Vergleich von

und 

zeigt noch, dass

und damit

ist.

2.3 Gleichmäßig beschleunigte Bewegung

Bewegungsgleichungen

Bei der untersuchten Bewegung ist festzustellen, dass in gleichen Zeitabschnitten sich die Geschwindigkeit stets um denselben Betrag ändert. Als Beschleunigung wird daher definiert:
 

Daraus ergibt sich die Maßeinheit:

.

Wenn wie im vorliegenden Fall die Beschleunigung konstant ist, heißt die Bewegung gleichmäßig beschleunigt. Beginnt die Bewegung zum Zeitpunkt t0 = 0 am Ort s0 = 0 aus der Ruhe heraus v0 = 0, dann lauten ihre Bewegungsgleichungen:

.

Diagramme

Das Zeit-Beschleunigung-Diagramm (t-a-Diagramm) ist bei einer gleichmäßig beschleunigten Bewegung sehr einfach: es ergibt sich eine Parallele zur t-Achse.

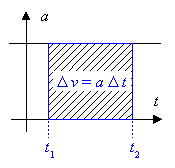
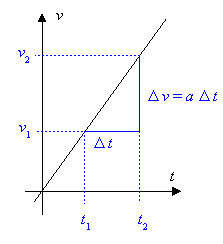
In diesem Diagramm lässt sich die in einem Zeitintervall  erfolgende Veränderung der Geschwindigkeit  finden: das Produkt

lässt sich geometrisch als eine Rechteckfläche deuten. Die Geschwindigkeitsänderung entspricht also der Rechteckfläche unter dem t-a-Graphen im t-a-Diagramm.

Im Zeit-Geschwindigkeits-Diagramm (t-v-Diagramm) lässt sich der in einem Zeitintervall  zurückgelegte Weg  finden: der Ausdruck

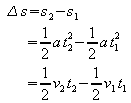
lässt sich geometrisch als Differenz von Dreieckflächen deuten. Der zurückgelegte Weg entspricht also Dreieckflächen und ihren Differenzen unter dem t-v-Graphen im t-v-Diagramm.

Berechnung der gleichmäßig beschleunigten Bewegung

Die Anfangsbedingungen seien t = 0, v = 0, s = 0 (Start am Koordinatenursprung aus der Ruhe heraus).

Von den 4 Größen t, a, v, s müssen 2 gegeben sein; die fehlenden 2 können dann wie folgt berechnet werden.
 
gegeben: Rechnung: Beispiel:

a, t

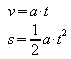 Ein Fahrzeug beschleunigt beim Start 8 s lang mit 1,3 m/s2. Welche Geschwindigkeit erreicht es und wie lang ist die Beschleunigungsstrecke?
 

a, v
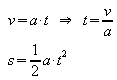 Ein Flugzeug beschleunigt beim Start mit 2 m/s2. Die zum Abheben erforderliche Geschwindigkeit ist 380 km/h. Wie lange dauert der Startvorgang und welche Länge muss die Startbahn haben?
 

a, s
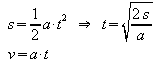 Ein Körper wird aus der Ruhe heraus mit 0,08 m/s2 gleichmäßig beschleunigt. In welcher Zeit legt er einen Weg von 100 m zurück und wie groß ist dann seine Geschwindigkeit?
 

v, t
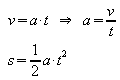 Eine Lokomotive fährt aus dem Ruhezustand beschleunigt an und erreicht nach 40 s die Geschwindigkeit 85 km/h. Wie groß ist die Beschleunigung und welche Entfernung vom Ausgangsort hat sie dann?
 

v, s
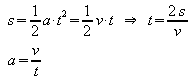 Ein Fahrzeug wird aus der Ruhe heraus gleichmäßig beschleunigt und erreicht nach einer Strecke von 80 m die Geschwindigkeit 20 m/s. Wie groß ist die Beschleunigung und wie lange dauert der Beschleunigungsvorgang?
 

s, t
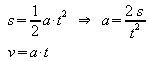 Auf einer geneigten Luftkissenfahrbahn durchfährt ein Gleiter aus der Ruhe heraus in 0,84 s die Strecke 1,0 m. Wie groß ist die Beschleunigung und welche Geschwindigkeit erreicht der Gleiter?

Ergänzung: In den Fällen, in denen die Zeit t unbekannt ist, kann auch die Methode der Elimination der Zeit verwendet werden.

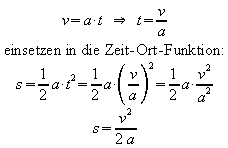
a) gegeben: a, s

b) gegeben: v, s

Beliebige Startwerte

Ein Körper bewege sich zur Zeit t0 = 0 mit der Geschwindigkeit v0. Wenn die konstante Beschleunigung a auf ihn einwirkt, so ergibt sich seine Geschwindigkeit v für jeden Zeitpunkt t wie folgt:

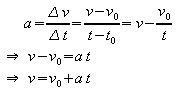
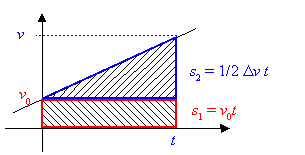
Die Rechteckfläche unter dem t-v-Graphen im t-v-Diagramm entspricht wieder dem zurückgelegten Weg, so dass sich die Zeit-Weg-Gleichung ergibt:

Da sich der Körper zur Zeit t0 = 0 schon an einem von Null verschiedenen Ort s0 befinden kann, ergibt sich als allgemeinste Zeit-Weg-Gleichung für die gleichmäßig beschleunigte Bewegung:

Beispiel: Beschreibung einer gleichmäßig beschleunigten Bewegung

Gegeben ist ein Zeit-Geschwindigkeit-Diagramm. Die Bewegung beginnt zur Zeit t0 = 0 am Ort
s0 = 0 aus der Ruhe heraus (v0 = 0).

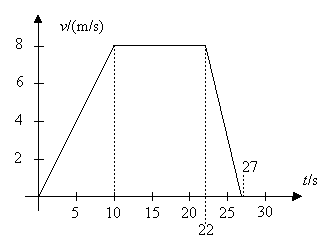
1) Im Zeitintervall t = 0 ... 10 s steigt die Geschwindigkeit linear an. Die Beschleunigung ist

.





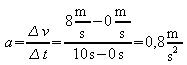Die zurückgelegte Strecke ergibt sich aus

.

Die Bewegungsgleichungen lauten

.

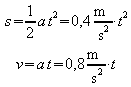2) Im Zeitintervall t = 10 s ... 22 s ändert sich die Geschwindigkeit nicht – es liegt also eine gleichförmige Bewegung vor. Die zurückgelegte Strecke kann aus der Fläche unter dem t-v-Graphen ermittelt werden:

Die Zeit-Ort-Gleichung lautet:

.

3) Im Zeitintervall t = 22 s ... 27 s nimmt die Geschwindigkeit linear ab. Die Beschleunigung nimmt deswegen einen negativen Wert an:

.

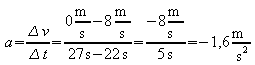Die zurückgelegte Strecke kann wieder aus der Fläche unter dem t-v-Graphen ermittelt werden:
.

Bewegungsgleichungen:

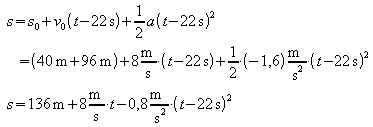
Übungen (1)

empfohlene Aufgaben aus dem Lehrbuch:

S.29, A2, A3, A4, A6

Übungen (2)

1. Ein Fahrzeug bewegt sich nach dem Start aus der Ruhe heraus 15 s lang mit einer konstanten Beschleunigung a und erreicht dabei die Endgeschwindigkeit v1.Mit dieser (jetzt konstanten) Endgeschwindigkeit bewegt sich das Fahrzeug weiter. 40 s nach dem Start hat das Fahrzeug 812,5 m zurückgelegt.

a) Skizzieren Sie das t-v-Diagramm.

b) Berechnen Sie die Beschleunigung a und die Endgeschwindigkeit v1.

2. In einem Autotest wird bei einem mit v0 = 100 km/h fahrenden PKW eine Vollbremsung durchgeführt. Der Bremsweg beträgt 49 m. Berechnen Sie die Beschleunigung a, wenn angenommen wird, dass die Beschleunigung während des Bremsvorgangs konstant ist.

3. Gegeben ist das t-v-Diagramm einer Bewegung.

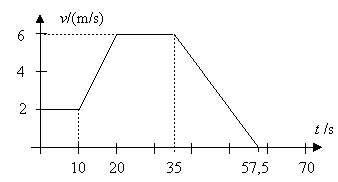
a) Beschreiben Sie die Bewegung.
b) Berechnen Sie die Beschleunigungen in den Zeitintervallen.
c) Berechnen Sie den jeweils in einem Zeitintervall zurückgelegten Weg.
d) Welche Entfernung hat der Körper zur Zeit t = 70 s vom Ausgangspunkt?

4. Gegeben ist das t-v-Diagramm einer Bewegung.

a) Beschreiben Sie die Bewegung.
b) Wie weit entfernt sich der Körper in positiver Bewegungsrichtung maximal vom Ausgangspunkt?
c) Wie weit ist der Körper zur Zeit t = 18 s vom Ausgangspunkt entfernt?
d) Nach welcher Zeit bewegt sich der Körper wieder durch den Ausgangspunkt?

Weitere Übungen

1. Ein Fahrzeug wird gleichmäßig beschleunigt; die Zeit-Weg-Funktion lautet

.

a) Welche Wegstrecke s1 legt das Fahrzeug in dem Zeitintervall D t1 von t0 = 0s bis t1 = 15 s zurück?
    Wie groß ist die Durchschnittsgeschwindigkeit in diesem Zeitintervall?
b) Wie lange dauert die Bewegung zwischen den Orten mit den Koordinaten s0 = 0 m und s2 = 25 m?
c) In welcher Zeitspanne Dt2,3 wird die Strecke zwischen den Orten mit den Koordinaten s2 = 25 m und s3 = 75 m zurückgelegt? Wie groß ist die Durchschnittsgeschwindigkeit in dieser Zeitspanne?
d) In welcher Zeitspanne Dt3,4 wird die Strecke zwischen den Orten mit den Koordinaten s3 = 75 m und s4 = 125 m zurückgelegt? Wie groß ist die Durchschnittsgeschwindigkeit in dieser Zeitspanne?
e) Welche Wegstrecke Ds5,6 wird in der Zeit von t5 = 17 s bis t6 = 42 s zurückgelegt?

2. Der Pfeil einer Armbrust wird längs einer 0,30 m langen Beschleunigungsstrecke auf die Endgeschwindigkeit 66,0 m/s beschleunigt. Vereinfachend wird angenommen, dass die Bewegung gleichmäßig beschleunigt ist. Wie lange dauert der Beschleunigungsvorgang?

3. Ein Flugzeug startet und erreicht nach der Rollstrecke von 2,6 km die zum Abheben nötige Geschwindigkeit von 340 km/h. Es wird angenommen, dass es sich um eine gleichmäßig beschleunigte Bewegung handelt.
Wie lange rollt das Flugzeug beim Startvorgang? Wie groß ist die Beschleunigung?

4. Ein PKW beschleunigt
a) aus der Ruhe heraus auf 80 km/h in 8,5 s,
b) von 100 km/h auf 120 km/h in 7,4 s,
c) von 120 km/h auf 140 km/h in 15,7 s.
Wie groß sind die mittleren Beschleunigungen in den einzelnen Zeitintervallen?

5. Ein Körper bewegt sich zur Zeit t = 0 mit der Geschwindigkeit v0 = 10 m/s längs einer geraden Bahn. Er wird dann (beginnend mit t = 0) abgebremst, d.h. seine Beschleunigung ist negativ:
a = –0,5 m/s2.
a) Zeichnen Sie das Zeit-Geschwindigkeit-Diagramm.
b) Ermitteln Sie aus der Zeichnung die Länge des Bremsweges sB, also die Länge des Weges, den der Körper von t = 0 bis zum Zeitpunkt des Stillstands zurücklegt.

6. Die Geschwindigkeit eines Zuges beträgt v0 = 120 km/h. Bei einer Notbremsung wird ein Bremsweg von 500 m zurückgelegt. Der Bremsvorgang kann als gleichmäßig beschleunigte Bewegung betrachtet werden.
a) Wie lange dauert es, bis der Zug zum Stillstand kommt?
b) Wie groß ist die Beschleunigung, die auf den Zug wirkt?

7. Von der US-Air-Force wurden 1954 Beschleunigungsversuche auf einer geraden Schienenstrecke durchgeführt, mit denen die Belastbarkeit des Menschen für Raumfahrtprojekte untersucht wurde. Ein Schlitten wurde mit Raketentriebwerken längs der Teilstrecke s1 = 840 m mit der Beschleunigung a = 70 m/s2 in Bewegung gesetzt. Auf einem zweiten Streckenteil der Länge s2 = 210 m wurde der Schlitten mit Bremsschaufeln, die in ein Wasserbecken eintauchten, abgebremst. Die Bewegungen können als gleichmäßig beschleunigt betrachtet werden.
a) Welche Geschwindigkeit erreichte der Schlitten am Ende der ersten Teilstrecke?
b) Wie lange dauerte der Beschleunigungsvorgang auf dieser Strecke?
c) Wie lange dauerte der Bremsvorgang auf der zweiten Teilstrecke?
d) Mit welcher Beschleunigung a2 wurde der Schlitten gebremst?
 

Lösungen

1.

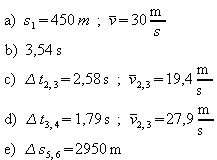
2.

3.

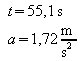
4.

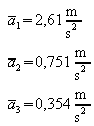
5. a)

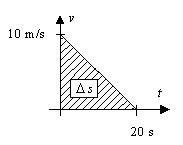
6.

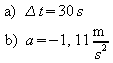
7.