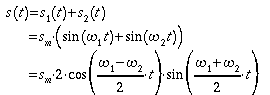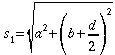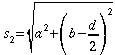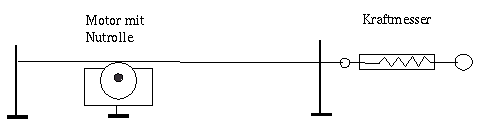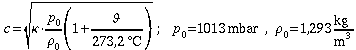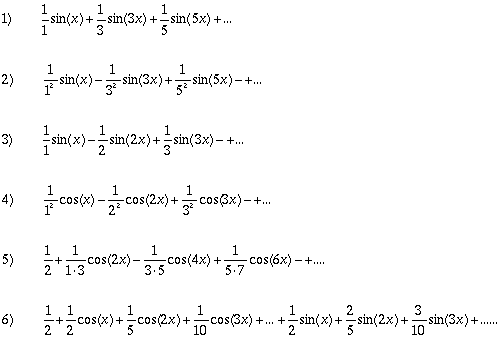Mechanische Schwingungen und
Wellen
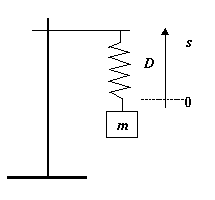
Das Federpendel
Eine
Schraubenfeder wird an einem Stativ befestigt und mit einem
Massenstück belastet. Das Massenstück wird im folgenden als
Pendelkörper bezeichnet.
|
|
Unter der Wirkung der Gewichtskraft des Pendelkörpers
wird die
Feder nach unten ausgelenkt, bis die Rückstellkraft der Feder die
Gewichtskraft des Pendelkörpers kompensiert. Die jetzige Lage des
Pendelkörpers definiert die Gleichgewichtslage des Pendels.
Ihr wird die Auslenkung (Elongation) s
= 0 zugeordnet. Die Auslenkungen werden nach oben positiv gezählt.
Eine
Verlängerung der Feder bedeutet dann einen negativen Wert der
Auslenkung: s < 0.
Nun wird der Pendelkörper entweder angehoben oder nach
unten
gezogen. Der Betrag der dabei erzielten maximalen Elongation wird Amplitude
genannt und mit 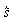 bezeichnet (gelesen: "s-Dach"). bezeichnet (gelesen: "s-Dach").
|
Wird
der Pendelkörper losgelassen beginnt die Pendelschwingung, d.h.
die periodische Hin- und Herbewegung des Pendelkörpers zwischen
zwei Umkehrpunkten. Da das schwingende System sich selbst
überlassen ist führt es eine freie Schwingung aus
(Gegensatz: erzwungene Schwingung unter der Wirkung
äußerer
Kräfte, etwa durch die Anregung mit einem Motor und Exzenter).
Als
Periodendauer (Schwingungsdauer) T wird die Zeit
für eine vollständige Pendelbewegung (Periode) bezeichnet,
also z.B. beginnend beim Punkt maximaler Auslenkung, Durchgang durch
die Ruhelage, Erreichen des Umkehrpunkts, erneuter Durchgang durch
die Ruhelage, Erreichen des Ausgangspunktes.
Beschreibung der Bewegung
a) Fertigen
Sie eine qualitative Skizze des Zeitverlaufes der Auslenkung s(t)
mit
folgenden
Anfangsbedingungen an: Zur Zeit t = 0
soll sich der Pendelkörper gerade durch die Gleichgewichtslage
(s = 0) nach oben (s > 0) bewegen.
b) Versuchen
Sie den Zeitverlauf der Geschwindigkeit v(t) des
Pendelkörpers zu skizzieren. (Anleitung: Wie groß ist wohl
die Geschwindigkeit in den Umkehrpunkten?
Was können Sie
über die Richtung der Bewegung und damit über das
Vorzeichen der Geschwindigkeit aussagen?
Wo wird die
Geschwindigkeit wohl am größten sein?)
c) Begründen
Sie, dass die Bewegung des Pendelkörpers eine beschleunigte
Bewegung ist. Skizzieren Sie den Zeitverlauf der Beschleunigung a(t).
Hinweis zu allen Messungen:
In
den folgenden Messungen soll jeweils die Periodendauer T
bestimmt werden. Bei kleinen Periodendauern empfiehlt es sich, die
Zeit für mehrere Perioden zu messen und diese Zeit dann durch
die Anzahl der gemessenen Perioden zu dividieren. So wird der
Messfehler bei der Bestimmung von T verringert.
Messung 1: Einfluss der
Amplitude 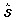 auf die
Periodendauer T
auf die
Periodendauer T
Verwenden
Sie für diese Messung die Feder 1.
Masse
des Pendelkörpers: m = __________ g = __________ kg
Stellen
Sie verschiedene Werte der Amplitude ein und messen Sie die
zugehörigen Periodendauern.
|
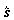 / m / m
|
T / s
|
|
|
|
|
|
|
|
|
|
|
|
|
Wie
hängt die Periodendauer demnach von der Amplitude ab?
Messung 2: Einfluss der Masse
m auf die Periodendauer T
Verwenden
Sie die gleiche Feder wie bei Messung 1.
Stellen
Sie verschiedene Massen des Pendelkörpers her und messen Sie die
zugehörigen Perioden-dauern.
Welcher
Zusammenhang von T und m ergibt sich daraus?
Messung 3: Einfluss der
Federkonstanten D auf die Periodendauer T
Die
bisher verwendete Feder wird als Feder 1 bezeichnet. Eine weichere
Feder heißt Feder 2, eine härtere Feder wird Feder 3
genannt. Von diesen drei Federn sind zuerst die Federkonstanten zu
bestimmen.
Im nächsten Schritt ist eine geeignete Masse des
Pendelkörpers zu wählen, so dass mit dieser Masse an allen
drei Federn die Periodendauer noch vernünftig bestimmt werden
kann.
m
= __________ g = __________ kg
Hängen
Sie diese Masse an die drei verschiedenen Federn und messen Sie die
zugehörigen Periodendauern. Welcher Zusammenhang von T
und D ergibt sich daraus?
|
Feder Nr.
|
D / (N/m)
|
T / s
|
|
1
|
|
|
|
2
|
|
|
|
3
|
|
|
Beschreibung der
Energieumwandlungen
a)
Um die Feder anfangs auf die Amplitude 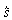 auszudehnen muss _______________arbeit verrichtet werden.
auszudehnen muss _______________arbeit verrichtet werden.
Diese
Arbeit ist dann in der Feder gespeichert als _______________energie.
Diese
berechnet sich aus der Formel ____________________
Bilden
Sie ein Beispiel unter Verwendung Ihrer Messdaten:
D
= __________ , 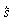 =
__________ , Energie: ____________________
=
__________ , Energie: ____________________
Lässt
man den Pendelkörper los, so verrichtet die Feder
_______________arbeit am Pendelkörper.
Dabei
wandelt sich die _______________energie der Feder um in
_______________Energie des Pendelkörpers.
Die
Umwandlung ist vollständig erfolgt, wenn der Pendelkörper
die Position s = __________
erreicht
hat. Danach wandelt sich die _______________Energie des
Pendelkörpers
um in
_______________energie
der Feder, und zwar so lange, bis der Pendelkörper die Position
s
= __________ erreicht hat.
b) Führen
Sie die weitere Beschreibung bis zum Wieder-Erreichen des
Startpunktes selbständig durch.
c) Wie
kann die größte Geschwindigkeit 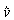 des
Pendelkörpers berechnet werden?
des
Pendelkörpers berechnet werden?
(Hinweis: Wenn von allen
Reibungsverlusten abgesehen wird, gilt der Energieerhaltungssatz der
Mechanik.)
Bilden
Sie ein Beispiel unter Verwendung Ihrer Messdaten:
Das Fadenpendel
Als
Fadenpendel (oder mathematisches Pendel) wird ein an
einem Faden aufgehängter Pendelkörper bezeichnet, wenn
folgende Voraussetzungen erfüllt sind:
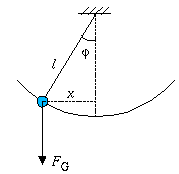
Der
Pendelkörper beschreibt einen Kreisbogen mit Radius l.
Zur
Beschreibung der periodischen Bewegung kann der Auslenkungswinkel 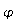 in Abhängigkeit von der Zeit benutzt werden.
in Abhängigkeit von der Zeit benutzt werden.
Die
Messung der Winkelamplitude kann indirekt durch Messung der
horizontalen Auslenkung erfolgen:
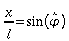 .
.
Messung 1: Einfluss der
Winkelamplitude 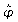 auf die
Periodendauer T
auf die
Periodendauer T
Masse
des Pendelkörpers: m = __________ g = __________ kg
Fadenlänge: l
= __________ cm
Stellen
Sie verschiedene Werte der Winkelamplitude ein und messen Sie die
zugehörigen Periodendauern.
|
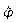 / m / m
|
T / s
|
|
|
|
|
|
|
|
|
|
|
|
|
Ist
eine Abhängigkeit der Periodendauer von der Winkelamplitude zu
erkennen?
Messung 2: Einfluss der Masse
m auf die Periodendauer T
Fadenlänge: l
= __________ cm
Winkelamplitude: 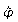 = _________
= _________
Verwenden
Sie verschiedene Kugeln unterschiedlicher Masse als Pendelkörper
und messen Sie die zugehörigen Periodendauern. Welcher
Zusammenhang von T und m ergibt sich daraus?
Messung 3: Einfluss der
Fadenlänge l auf die Periodendauer T
Masse
des Pendelkörpers: m = __________ g = __________ kg
Winkelamplitude: 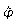 = _________
= _________
Stellen
Sie verschiedene Fadenlängen ein und messen Sie die
zugehörigen
Periodendauern.
Welcher
Zusammenhang von T und l ergibt sich daraus?
Woher
kommt beim Fadenpendel die Rückstellkraft?
Wie
würden sich die von Ihnen untersuchten Fadenpendel auf dem Mond
verhalten?
Welche
Größe beeinflusst demnach die Periodendauer?
Versuchen
Sie mit Ihren bisherigen Erkenntnissen eine Formel für die
Schwingungsdauer des Fadenpendels zu entwickeln.
Bestimmen
Sie eventuell benötigte konstante Faktoren aus Ihren Messwerten.
Schwingungen einer Wassersäule
Material:
|
Stativfuß
Schraubmuffe U-Rohr
Schieblehre
Stativstange Schraubhalter
Messzylinder Stoppuhr
|
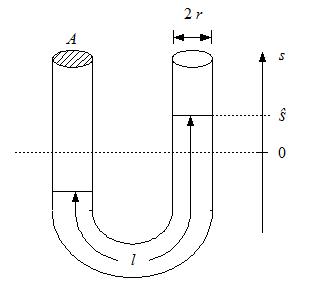
1. Stellen
Sie das U-Rohr mit Hilfe des Stativmaterials aufrecht stehend auf.
2. Bestimmen
Sie den Innenradius r des U- Rohrs.
r
= _______________
Das
U-Rohr stellt einen gebogenen Zylinder dar. Für ein
eingefülltes Wasservolumen gelten daher die Zylinderformeln.
3. Füllen
Sie ein mit dem Messzylinder abgemessenes Wasservolumen in das
U-Rohr ein.
Versetzen
Sie die Wassersäule in Schwingungen und messen Sie die
Periodendauer T:
-
Messen Sie die Zeit für mehrere Perioden und teilen Sie
durch
die Anzahl der Perioden.
-
Wiederholen Sie diese Messung für jedes Volumen dreimal.
-
Bilden Sie aus den drei Einzelwerten den Mittelwert und tragen
Sie diesen als Messergebnis in die Tabelle ein.
4. Stellen
Sie die Messergebnisse in einem V-T-Diagramm dar (V
nach rechts, T nach oben).
Bestimmen
Sie den Zusammenhang von T und V:
T
~ _______________
Tragen
Sie die Rechnung zur Überprüfung Ihrer Vermutung in die
dritte Tabellenspalte ein.
5. Berechnen
Sie zu jedem Volumen die Länge l der
Wassersäule.
6. Zeigen
Sie theoretisch, dass gilt :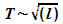 .
.
7. Betrachten
Sie die Einheiten in der Proportionalität von 6. Welche
physikalische Größe könnte demnach in der Beziehung
für die Periodendauer noch fehlen?
T
~ _______________
8. An
der Gesetzmäßigkeit für die Periodendauer der
Schwingung der Wassersäule fehlt jetzt noch ein Zahlenfaktor.
Versuchen Sie, diesen zu bestimmen.
Schwebung
Material:
|
2 Stimmgabeln auf Resonanzkörpern
Zusatzmasse
Anschlaghammer
|
Zweikanal-Oszilloskop
Sondenmikrofon
2
Tonfrequenzgeneratoren
2 Lautsprecher
|
|
Prüfen Sie vor der erstmaligen Verwendung des
Oszilloskops, ob
die Zeitbasis kalibriert ist.
Bilden Sie dazu das Signal des
Tonfrequenzgenerators mit f = 1 kHz ab und
messen Sie die Periodendauer.
|
Demonstration einer Schwebung
Eine
Schwebung entsteht bei der Überlagerung von zwei harmonischen
Schwingungen mit
- gleicher Amplitude
- verschiedener Frequenz.
Das
Ergebnis dieser Überlagerung läßt sich leicht mit
zwei etwas verstimmten Stimmgabeln deutlich machen. Wegen der
unterschiedlichen Wellenlängen kommt es abwechselnd zur
destruktiven und konstruktiven Interferenz. Das zu hörende
periodische Auf- und Abschwellen der Lautstärke bezeichnet man
als Schwebung.
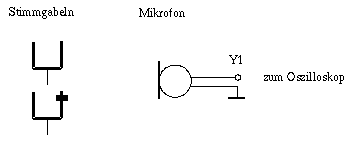
Verschieben
Sie die Zusatzmasse auf der zweiten Stimmgabel, schlagen Sie beide
Stimmgabeln an und prüfen Sie mit dem Gehör, ob eine gut
wahrnehmbare Schwebung entsteht. (Das Oszilloskop bleibt hier
zunächst ausgeschaltet.)
Mathematische Darstellung der
Schwebung
Am
Ort des Mikrofons überlagern sich die von den Stimmgabeln
ausgehenden Schallwellen. Da der
Ort gleich ist, genügt es
die zeitabhängigen Schwingungen an diesem Ort zu betrachten.
Angenommen,
die beiden Stimmgabeln schwingen harmonisch mit gleicher Amplitude,
gleicher Phase und den verschiedenen Frequenzen f1
und f2. Dann gilt für die Schwingungen am
Mikrofon:
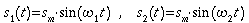 .
.
Die
Überlagerung ergibt mit dem Additionstheorem des Sinus:
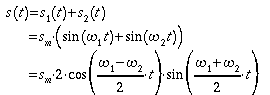
Diese
Gleichung beschreibt eine Schwingung der Amplitude 2sm
mit der mittleren
Frequenz
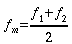 .
.
Diese
wird mit einer niederfrequenten Kosinusschwingung multipliziert, d.h.
ihre Amplitude wird im Takt einer Kosinusschwingung
vergrößert
und verkleinert. Man sagt, die Schwingung ist moduliert.
Die Frequenz der Modulation beträgt (f1 - f2)
/
2.
Da man eine positive Amplitude nicht
von einer negativen unterscheiden kann, hört man ein doppelt so
schnelles Auf- und Abschwellen der Lautstärke. Zu hören ist
also eine Schwebungsfrequenz, die der Differenzfrequenz
entspricht:
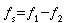 .
.
Messungen
A)
-
Die Schwingung einer Stimmgabel soll auf dem Oszilloskop
abgebildet werden. Dabei geht es
zunächst darum, geeignete Einstellungen des Oszilloskops zu
finden, daß
die Schwingung gut
erkennbar dargestellt wird. Dann kann die Periodendauer mit dem
Oszilloskop gemessen und daraus die Frequenz der Stimmgabel bestimmt
werden.
T1
= __________ f1 = __________
T2
= __________ f2 = __________
Tm
= __________ fm = __________
Ts
= __________ fs = __________
B)
Statt
der Stimmgabeln werden jetzt 2 Tonfrequenzgeneratoren und zwei
Lautsprecher verwendet.
Damit sind dieselben Messungen wie für
die Stimmgabeln durchzuführen.
T1
= __________ f1 = __________
T2
= __________ f2 = __________
Tm
= __________ fm = __________
Ts
= __________ fs = __________
Erzwungene Schwingungen
Material:
|
Feder
Kugel
Faden
|
Drehpendel
Kraftmesser 0,1 N
Stoppuhr |
Netzgerät
Messgeräte für Spannungen
|
Stößt
man ein schwingungsfähiges System an und überlässt es
sich dann selbst, so führt es eine freie Schwingung aus.
Die Frequenz der freien Schwingung wird auch als Eigenfrequenz
bezeichnet.
Wird
ein schwingungsfähiges System von einem äußeren
Antrieb periodisch erregt, spricht man von erzwungenen
Schwingungen, da der äußere Antrieb dem System seine
Frequenz aufzwingt. Im eingeschwungenen Zustand antwortet der
Oszillator nicht mehr mit seiner Eigenfrequenz, sondern schwingt mit
der Fremdfrequenz des Erregers.
Vorversuch
Versetzen
Sie ein Federpendel (oder ein Fadenpendel) in Schwingungen, indem Sie
den Aufhängepunkt auf und ab (bzw. hin und her) bewegen.
Bei
niedrigen Anregungsfrequenzen (Zeitlupenschwingung der Hand) kann das
Pendel der Anregung vollständig folgen. Erreger und Oszillator
schwingen als Ganzes. Sie schwingen mit gleicher Amplitude und
befinden sich im Gleichtakt: die Phasenverschiebung
beträgt
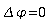 .
.
Geht
man zu hohen Anregungsfrequenzen über, kann der Oszillator
infolge seiner Trägheit der Anregung immer schlechter folgen.
Die Amplitude des Oszillators geht gegen Null; Antrieb und Schwingung
erfolgen im Gegentakt: die Phasenverschiebung beträgt 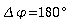 .
.
Stimmen
Erreger- und Eigenfrequenz überein, dann schaukelt sich der
Oszillator zu Amplituden auf, welche die Anregungsamplitude weit
übersteigen. Der Grund dafür ist, dass die Energiezufuhr
immer im genau gleichen Takt und zum richtigen Zeitpunkt erfolgt.
Dieses maximale Mitschwingen bezeichnet man als Resonanz. Im
Resonanzfall hinkt der Oszillator der Erregerschwingung um eine
Viertelperiode hinterher: die Phasenverschiebung beträgt 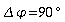 .
.
Erzwungene Schwingungen eines
Drehpendels
|
Zur quantitaven Untersuchung erzwungener Schwingungen wird
hier ein Drehpendel verwendet. Es ist ein Schwingungssystem,
das in mechanischen Armbanduhren für den Gleichlauf der Uhr sorgt.
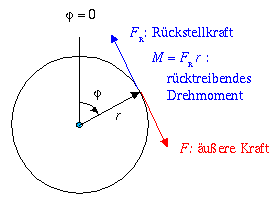
Das Drehpendel ist ein weiteres Beispiel für einen
harmonischen Oszillator: hier ist das rücktreibende Drehmoment
proportional zum Drehwinkel: 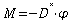 . (Erläuterung des
Begriffes
"Drehmoment" siehe bei der Aufgabe "Drehbewegung starrer Körper").
Die
Größe D* heißt Winkelrichtgröße. . (Erläuterung des
Begriffes
"Drehmoment" siehe bei der Aufgabe "Drehbewegung starrer Körper").
Die
Größe D* heißt Winkelrichtgröße.
|
|
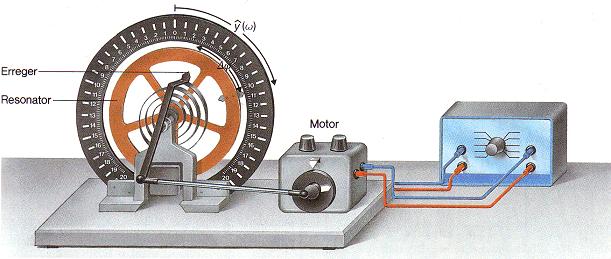
Aufbau:
Bei
dem in der folgenden Abbildung gezeigten Drehpendel lässt sich
die Anregung kontrolliert mit konstanter Amplitude über einen
regelbaren Motor durchführen; eingestellt wird dazu die Spannung
Uprüf. Die Dämpfung der Schwingung wird
durch eine Wirbelstrombremse hervorgerufen. Die Stärke der
Dämpfung wird mit der Spannung Ud eingestellt.
Messungen:
(1) Bestimmen
Sie die Winkelrichtgröße 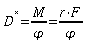 .
.
Befestigen
Sie dazu mit einem dünnen Faden einen Kraftmesser am Zeiger des
Resonators. Ziehen Sie so am Kraftmesser, dass die Wirkungslinie der
Kraft stets tangential zum Rand des Resonators verläuft (s.
obige Skizze). Verdrehen Sie den Resonator um einen bestimmten
Winkel.
r = __________ F = __________ M = __________
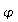 = _________
= _________
D*
= __________
(2) Bestimmen
Sie die Eigenfrequenz des ungedämpften Drehpendels: Lenken Sie
dazu den Resonator um einen beliebigen Winkel aus und messen Sie die
Periodendauer.
T
= __________ f = __________
Für
die Periodendauer des Drehpendels gilt die Beziehung
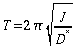 .
.
Dabei
ist J das Trägheitsmoment des Resonators.
Bestimmen Sie J unter Verwendung Ihrer Messwerte für T
und D*.
(3) Demonstrieren
Sie den Einfluss der Dämpfung bei der freien Schwingung des
Drehpendels. Stellen Sie nacheinander die Dämpfungsspannungen Ud
= 2 V und Ud = 4 V ein. Beobachten Sie das
Verhalten des Pendels und vergleichen Sie mit der freien Schwingung
des ungedämpften Pendels. Messen Sie jeweils die zugehörigen
Peridendauern T2 bzw. T4.
T2
= __________ T4 = __________
Vergleichen
Sie mit der Periodendauer der freien, ungedämpften Schwingung.
Erläutern Sie gegebenenfalls Unterschiede.
(4) Resonanzkurven:
Nehmen Sie die Amplitude des Resonators und seine Phasenverschiebung
zum Erreger in Abhängigkeit von der Erregerfrequenz auf. Stellen
Sie dazu die Dämpfungsspannung auf den Wert
Ud
= 2 V.
Stellen
Sie dann den Erreger mit den in der Tabelle angegebenen Werten von
Uprüf ein und messen Sie Periodendauer Terr
des Erregers, Amplitude 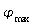 des Resonators und Phasenverschiebung
des Resonators und Phasenverschiebung 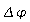 zwischen Resonator und Erreger. (Skt: Skalenteile)
zwischen Resonator und Erreger. (Skt: Skalenteile)
|
Uprüf / V
|
Terr / s
|
ferr / Hz
|
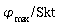
|
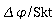
|
|
7,40
|
|
|
|
|
|
7,60
|
|
|
|
|
|
7,80
|
|
|
|
|
|
7,90
|
|
|
|
|
|
8,00
|
|
|
|
|
|
8,10
|
|
|
|
|
|
8,20
|
|
|
|
|
|
8,40
|
|
|
|
|
|
8,60
|
|
|
|
|
|
8,80
|
|
|
|
|
|
9,00
|
|
|
|
|
|
9,20
|
|
|
|
|
Stellen
Sie die Amplitude des Resonators und seine Phasenverschiebung zum
Erreger jeweils in Abhängigkeit von der Erregerfrequenz in zwei
Diagrammen dar.
(Wenn
noch Zeit ist: Wiederholen Sie die Messung für eine stärkere
Dämpfung.)
Schallwellen
Material:
|
Tonfrequenzgenerator
2 Lautsprecher
Zweikanal-Oszilloskop
Sondenmikrofon
|
Maßstab
Winkelmesser
Stativmaterial |
Prüfen
Sie
vor
der erstmaligen Verwendung des Oszilloskops, ob die Zeitbasis
kalibriert ist.
Bilden Sie dazu das Signal des Tonfrequenzgenerators
mit f = 1 kHz ab und messen Sie die Periodendauer. |
1. Interferenz von
Schallwellen
Untersucht
wird die Überlagerung (Interferenz) kohärenter
Wellenzüge, d.h. von Wellenzügen mit gleicher
Amplitude, gleicher Frequenz und fester (zeitlich konstanter)
Phasendifferenz am Beispiel von Schallwellen.
Zwei
Lautsprecher werden in Reihe an einen Tonfrequenzgenerator
geschaltet.
Abstand der Lautsprecher: d = 40
cm.
Generatorfrequenz: f = 4
kHz. Zur genauen Einstellung der Frequenz wird ein Oszilloskop
verwendet.
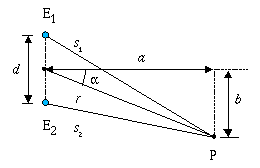
Nach
der Einstellung von f wird das Oszilloskop an das
Sondenmikrofon geschaltet, mit dem das Wellenfeld vermessen wird.
Messgrößen sind:
-
Abstand r des Punktes im Wellenfeld vom Mittelpunkt der
Verbindungsstrecke der beiden Lautsprecher;
-
Winkel 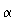 , unter dem der Punkt zur Mittelsenkrechten
der
Verbindungsstrecke der beiden Lautsprecher erscheint.
, unter dem der Punkt zur Mittelsenkrechten
der
Verbindungsstrecke der beiden Lautsprecher erscheint.
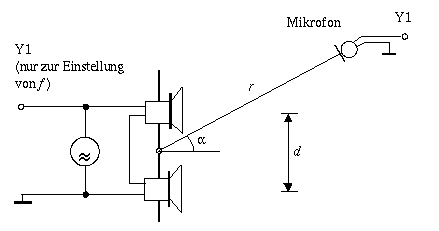
Der
Gangunterschied der von den beiden Lautsprechern ausgehenden
Schallwellen ergibt sich wie folgt.
Messen
Sie zu mehreren Interferenzmaxima und -Minima r und 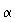 .
.
Ermitteln
Sie daraus die Schallgeschwindigkeit in Luft.
Die
Schallgeschwindigkeit in Luft ist abhängig von der Temperatur.
Der theoretische Wert errechnet sich aus
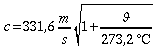 .
.
Vergleichen
Sie den theoretischen Wert mit Ihrem Messwert.
2. Messung der
Schallgeschwindigkeit
Aufbau:
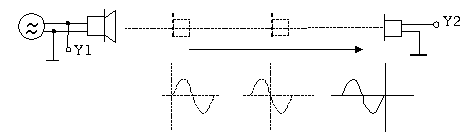
An
den Tonfrequenzgenerator wird ein Lautsprecher angeschlossen.
Außerdem wird das Signal oszillographiert, um die Periodendauer
(und damit die Frequenz) möglichst genau bestimmen zu können.
Ein Mikrofon wird an Kanal 2 des Oszilloskops angeschlossen. Wird es
vom Lautsprecher entfernt, vergrößert sich der Laufweg der
Schallwelle vom Lautsprecher zum Mikrofon. Wenn das Oszilloskop auf
Kanal 1 getriggert wird, läuft daher das Signal des Mikrofons
auf dem Bildschirm nach links.
a)
Stellen Sie die Frequenz f = 10 kHz ein.
b)
Stellen Sie das Mikrofon in etwa 15 cm Entfernung vor den
Lautsprecher. Wenn das Signal auf Kanal 2 zu klein sein sollte,
aktivieren Sie die Vergrößerung "Y-Mag x 5".
c)
Schieben Sie das Mikrofon so, das auf dem Bildschirm das Signal
sinusförmig durch den Nullpunkt verläuft.
d)
Entfernen Sie nun das Mikrofon vom Lautsprecher und messen Sie
jeweils die Verschiebungslänge, nach der das Mikrofonsignal
einmal mit einer ganzen Periode durch den Nullpunkt hindurch nach
links gewandert ist. Dies ist die Wellenlänge der Welle.
e)
Bilden Sie den Mittelwert der einzelnen 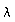 -Messungen
und bestimmen Sie die Schallgeschwindigkeit. Vergleichen Sie mit dem
theoretischen Wert.
-Messungen
und bestimmen Sie die Schallgeschwindigkeit. Vergleichen Sie mit dem
theoretischen Wert.
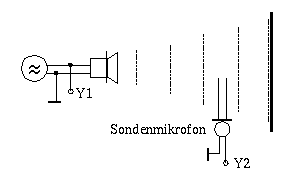
3. Stehende Schallwellen
Ein
Lautsprecher wird in etwa 2 m Abstand senkrecht vor einer Wand
aufgestellt. Mit einem Tonfrequenzgenerator wird eine Schallwelle im
kHz-Bereich erzeugt. Die Amplitude des Wellenfeldes wird mit einem
Sondenmikrophon mit angeschlossenem Oszilloskop ausgemessen. Fährt
man das Schallfeld mit dem Mikrofon ab, so zeigt das Oszilloskop in
Abhängigkeit vom Abstand zur Wand minimale bzw. maximale
Amplituden an.
a) Stellen
Sie den Tonfrequenzgenerator auf die gewünschte Frequenz ein.
Zur genauen Einstellung der Frequenz verwenden Sie das Oszilloskop.
b) Schalten
Sie das Mikrofon auf Kanal 2 des Oszilloskops. Bestimmen Sie die
Position mehrerer Knoten.
c) Ermitteln
Sie aus dem Abstand je zwei aufeinander folgender Knoten die
Wellenlänge der Welle.
d) Berechnen
Sie den Mittelwert der Wellenlänge.
e) Bestimmen
Sie mit den vorliegenden Daten die Schallgeschwindigkeit in Luft und
vergleichen Sie mit dem theoretischen Wert nach der Formel aus
Versuch 1.1.
Stehende Seilwellen
Material:
|
Motor
Nutrolle
langes Gummiseil
Kraftmesser 10 N
Maßstab (2 m) oder Bandmaß
Stroboskop
|
3 Tischzwingen
3 kurze Stativstangen
2 Stativfüße
2 lange Stativstangen
|
Aufbau:
Befestigen
Sie den Motor mit einer Tischzwinge an der Vorderkante des
Experimentiertisches. Als Exzenter wird eine Nutrolle benutzt.
Bringen Sie an der Hinterkante des Experimentiertisches und an einem
Arbeitstisch am Ende des Raumes mit Tischzwingen zwei kurze
Stativstangen an. Das Gummiseil wird an der Stange hinter dem Motor
befestigt und über die Nutrolle geführt. Am anderen Ende
des Seils wird der Kraftmesser befestigt. Spannen Sie nun das Seil
mit der gewünschten Kraft und befestigen Sie dann das lose Ende
an der zweiten Stativstange.
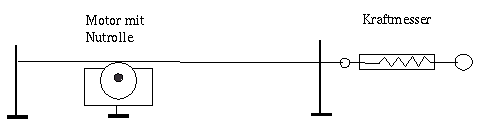
Die
Drehzahl des Motors kann kontinuierlich geregelt werden. Damit ist
dann auch die Frequenz der Seilwelle, die durch den Exzenter
angegeregt wird, bekannt. Die Frequenz wird mit einem Stroboskop
ermittelt.
Messungen:
1. Spannen
Sie das Gummiseil mit F = 2,5 N.
Erzeugen
Sie dann die Grundschwingung (1. Harmonische) und die 2. und 3.
Harmonische des Seils.
Bestimmen
Sie jeweils die Wellenlänge aus dem Abstand zweier
Schwingungsknoten und ermitteln Sie die Phasengeschwindigkeit der
Seilwelle.
|
k
|
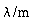
|
f / Hz
|
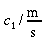
|
|
1
|
|
|
|
|
2
|
|
|
|
|
3
|
|
|
|
Mittelwert:

2. Wiederholen
Sie die Messungen für die Spannkraft F = 5,0 N.
|
k
|
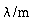
|
f / Hz
|
|
|
1
|
|
|
|
|
2
|
|
|
|
|
3
|
|
|
|
Mittelwert:

Auswertung:
Wie
hängt die Phasengeschwindigkeit c der Seilwelle von der
Spannkraft F ab?
Eigenschwingungen einer Luftsäule
(Kundt'sches Rohr)
Material:
Tonfrequenzgenerator
Lautsprecher
Oszilloskop
|
Kundt-Rohr
Korkmehl
Stempel
Maßstab |
Prüfen
Sie
vor
der erstmaligen Verwendung des
Oszilloskops, ob die Zeitbasis kalibriert ist.
Bilden Sie dazu das
Signal des Tonfrequenzgenerators mit f = 1 kHz ab und messen
Sie die Periodendauer. |
Stehende
Longitudinalwellen sind z.B. die Eigenschwingungen von Luftsäulen.
Bei diesen lassen sich Knoten und Bäuche gut in der Kundt'schen
Röhre beobachten.
Vor
einem offenen oder halboffenen Glasrohr, das feinverteiltes trockenes
Korkmehl enthält, wird ein Lautsprecher aufgestellt, der mit
einem Tonfrequenzgenerator verbunden ist. Die Frequenz des Generators
wird oszillographisch bestimmt.
Das
zweite Ende des Rohrs wird mit einem verschiebbaren Stempel
verschlossen.

a) Stellen
Sie bei fester Position des Stempels Frequenzen ein, bei denen sich
stehende Wellen ergeben. Die Bäuche und Knoten sind an den
Kundt'schen Staubfiguren zu erkennen.
b) Bestimmen
Sie aus den Staubfiguren die Wellenlänge und ermitteln Sie die
Schallgeschwindigkeit in Luft.
c) Stellen
Sie die feste Frequenz f = 1 kHz ein. Schieben Sie den Stempel
dann langsam weiter in das Rohr hinein, bis sich stehende Wellen
ausbilden. Messen Sie auch hier die Wellenlänge und bestimmen
Sie wieder die Schallgeschwindigkeit.
Vergleichen
Sie den erhaltenen Wert für die Schallgeschwindigkeit mit dem
theoretischen Wert, der sich aus der folgenden Formel ergibt.
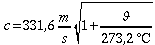
Bestimmen
Sie weiter den Wert von k in
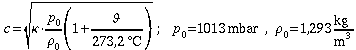
d) Entfernen
Sie den Stempel aus dem Rohr und stellen Sie Frequenzen ein, die zur
Ausbildung stehender Wellen führen.
Monochord / Spannkraft einer Saite
Material:
Monochord
Tonfrequenzgenerator
Lautsprecher
Oszilloskop |
Schublehre
Maßstab
|
Prüfen
Sie
vor
der erstmaligen Verwendung des Oszilloskops, ob
die Zeitbasis kalibriert ist.
Bilden Sie dazu das Signal des
Tonfrequenzgenerators mit f = 1 kHz ab und messen Sie die
Periodendauer. |
Eine
zweiseitig eingespannte Saite wird durch Anzupfen in der Mitte in
ihrer Grundschwingung erregt (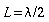 ).
Für die Phasengeschwindigkeit c einer Transversalwelle
auf einer gespannten Saite gilt
).
Für die Phasengeschwindigkeit c einer Transversalwelle
auf einer gespannten Saite gilt
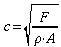 ,
,
F: Spannkraft;
rho: Dichte der Saite (Stahl: 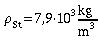 );
);
A: Querschnittsfläche der
Saite
A)
Messen
Sie die Daten der Monochordsaite mit dem höheren Ton:
Saitenlänge: L = _______________
Drahtdurchmesser:
d = _______________
Saitenquerschnitt: A = _______________
B)
Lassen
Sie die Saite schwingen. Stimmen Sie den Tonfrequenzgenerator auf die
Saitenfrequenz ab. Ermitteln Sie mit der Schwebungsmethode die
Frequenz der Saite. Das Signal des Generators wird oszillographiert,
um die Frequenz möglichst genau zu ermitteln.
f
= _______________
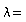 ______________
______________
Bestimmen
Sie die Phasengeschwindigkeit c der Transversalwelle auf der
gespannten Saite.
c
= _______________
Ermitteln
Sie die Spannkraft F , mit der die Saite gespannt ist.
F
= _______________
C)
Wiederholen
Sie die Messungen für die Monochordsaite mit dem tieferen Ton.
Rechnerversuch zur Fourier-Synthese
Es
soll mit Rechnerunterstützung untersucht werden, was geschieht,
wenn mehrere sinusförmige
Wellen überlagert werden mit
den Eigenschaften:
- gleiche Ausbreitungs- und Schwingungsrichtung
- verschiedene Amplitude
- verschiedene Frequenzen (Wellenlängen).
Würde
man dabei beliebige Frequenzen (Wellenlängen) zulassen, so
wäre
das Ergebnis von vornherein klar: es ergäbe sich ein
heilloses Durcheinander. Als einschränkende Zusatzbedingung
sollgefordert werden, dass die Frequenzen (Wellenlängen) nur
ganzzahlige Vielfache einer Grundfrequenz f1
(Grundschwingung l1)
sein
sollen.
Die
Frequenzen fn
= n.f1
bezeichnet man als Harmonische der Grundfrequenz f1
(analog für lk).
Jede
Funktion F(t), welche die Periode T hat, kann zu
einer Funktion mit der Periode 2pi
gemacht werden.
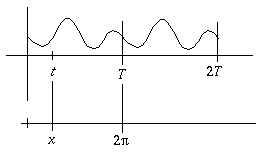
Die
volle Periode T entspricht 2pi,
dann verhalten sich t und x entsprechend:
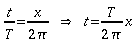 .
.
Damit
wird dann
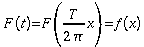
zu
einer Funktion der Variablen x und diese Funktion hat die
Periode 2pi.
Ein
in Physik und Technik sehr oft benötigter Zusammenhang ist der
|
Satz von Fourier: Jeder beliebige periodische
Vorgang läßt sich eindeutig aus Sinus- und
Cosinusschwingungen
zusammensetzen.
|
Da
stets auf die Periode 2pi
transformiert werden kann, genügt die Betrachtung von Funktionen
mit dieser Periode.
Die
Durchführung der im Satz angesprochenen Zerlegung wird auch als
Fourier-Analyse bezeichnet. Hier soll umgekehrt
untersucht werden, was die Zusammensetzung verschiedener Sinus-
und Cosinusschwingungen ergibt (Fourier-Synthese). Dazu
bildet man Fourier-Summen:
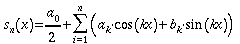
A)
Die
folgenden Beispiele sollen mit dem Rechner untersucht werden.
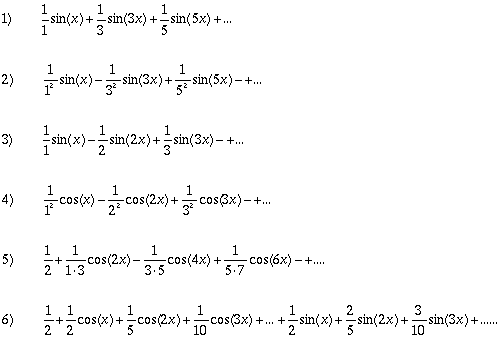
In
x-Richtung soll von 0 bis 4pi
dargestellt werden. Als Schrittweite ist z.B. dx = 0,05
geeignet. Die Berücksichtigung der Summanden bis n
= 11 reicht aus.
Fragen:
1) Was
für periodische Vorgänge werden durch diese Fourier-Summen
näherungsweise dargestellt?
2) Wie
unterscheiden sich die Funktionen, die sich rein aus
Sinus-Koeffizienten und Funktionen, die sich rein aus
Cosinus-Koeffizienten zusammensetzen?
B)
1) Setzen
Sie alle Koeffizienten auf Null. Geben Sie dann die
Cosinus-Koeffizienten a5 = a6 = 1
ein. Erläutern
Sie, wie die entstehende Funktion zustande kommt. Hinweis: Es gilt
das folgende Additionstheorem:
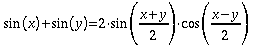 .
.
2) Vergleichen
Sie mit der Funktion, die nur mit a9 = a10
= 1 bzw. nur mit a2
= a3 = 1 gebildet wird.
3) Setzen
Sie wieder nur a5 = a6 = 1.
Ergänzen Sie dann schrittweise:
a4
= a7 = 0,53,
a3
= a8 = 0,12.
Wie
ändert sich die Funktion gegenüber der Darstellung mit nur
2 Koeffizienten a5 = a6 = 1?
Achten
Sie auf die Einhüllende.

![]() bezeichnet (gelesen: "s-Dach").
bezeichnet (gelesen: "s-Dach").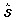 auf die
Periodendauer T
auf die
Periodendauer T
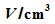
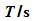
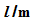
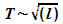 .
.