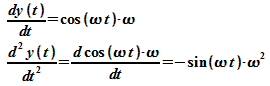Ableitung und Differentialquotienten

1. Begriff der Ableitung

Bei einer Geraden mit der Gleichung ist m bekanntlich die Steigung der Geraden. Diese Steigung ist definiert durch den Differenzenquotienten

Die Steigung des Graphen einer Funktion f in einem Punkt P₁(x | f (x)) wird näherungsweise auch durch einen Differenzenquotienten ermittelt, indem ein zweiter Punkt auf dem Graphen P₂ gewählt wird. Die Gerade durch die beiden Punkte P₁ und P₂ heißt Sekante. Die Steigung der Sekante ist ein Näherungwert für die Steigung des Graphen im Punkt P₁:

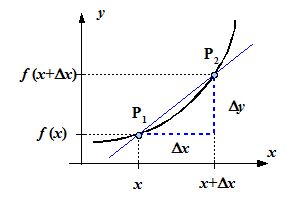
Die gesuchte Steigung im Punkt P₁ wird umso genauer erhalten, je näher der Punkt P₂ am Punkt P₁ liegt, oder anders gesagt: je kleiner x ist. Wenn x immer kleiner wird, nähert sich die Sekante durch P₁ und P₂ immer mehr der Tangente des Graphen im Punkt P₁ an. In der Mathematik wird dafür geschrieben:

Dieser sogenannte Grenzwert (Limes) des Differenzenquotienten heißt Ableitung der Funktion f an der Stelle x. Die geometrische Bedeutung dieser Ableitung ist die Steigung der Tangente an den Graphen der Funktion f an der Stelle x.

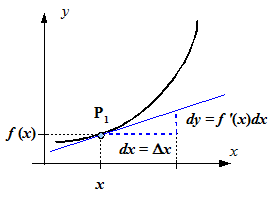
In der Physik und in der Technik wird häufig eine andere Schreibweise verwendet:

Dabei werden dy (bzw. df) und dx als Differentiale bezeichnet. Die Ableitung wird daher auch Differentialquotient genannt. Die geometrische Bedeutung der Differentiale ist der folgenden Abbildung zu entnehmen.

2. Anwendung in der Physik

In der Physik treten oft zeitabhängige Größen auf. Bei zeitabhängigen Größen interessiert man sich meistens auch für die Änderungsrate, also die Veränderung des Wertes der Größe bezogen auf die Zeit. Ein einfaches mechanisches Beispiel ist die geradlinige, ungleichförmige Bewegung eines Körpers. Zur Beschreibung dieser Bewegung wird eine Zeit-Ort-Funktion s(t) benutzt. Als Durchschnittsgeschwindigkeit wird die Änderungsrate von Ortskoordinate und Zeit, also der Differenzenquotient

definiert. Die Momentangeschwindigkeit ergibt sich durch Grenzwertbildung des Differenzenquotienten:

Mit der Schreibweise der Differentialquotienten also:

In Worten bedeutet dies: Die Zeit-Geschwindigkeitsfunktion ist die Ableitung der Zeit-Ortsfunktion nach der Zeit.

Der Begriff der Beschleunigung wird definiert als Veränderung der Geschwindigkeit mit der Zeit. Die Durchschnittbeschleunigung kann daher mit einem Differenzenquotienten angegeben werden:

Die Momentanbeschleunigung ergibt sich durch Grenzwertbildung des Differenzenquotienten:

Die Zeit-Beschleunigungsfunktion ist also die Ableitung der Zeit-Geschwindigkeitsfunktion. Da die Zeit-Geschwindigkeitsfunktion ihrerseits die Ableitung der Zeit-Ortsfunktion ist, kann man dies auch so ausdrücken, dass die Zeit-Beschleunigungsfunktion die zweite Ableitung der Zeit-Ortsfunktion ist. Mit Differentialquotienten wird die zweite Ableitung wie folgt geschrieben:

Als einfaches Beispiel soll die gleichmäßig beschleunigte Bewegung betrachtet werden:

3. Kettenregel

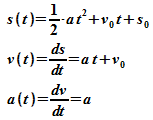
Die Ableitungen der Winkelfunktionen Sinus und Kosinus lauten:

In physikalischen Anwendungen kommen diese Funktionen häufig vor, aber nicht in der „reinen“ Form, sondern in Form einer Verkettung von zwei Funktionen, z.B.:

Hier bedeutet t die Zeit;  ist eine Konstante mit der Maßeinheit s^-1 und ist eine einfache lineare Funktion. Man sagt, die Sinusfunktion und die lineare Funktion sind miteinander verkettet und bezeichnet die Sinusfunktion als die äußere Funktion und die lineare Funktion als innere Funktion:

Beispiel:

Bildet man zur Bestimmung der Ableitung versuchsweise

so lässt sich an den Graphen erkennen, dass dies nicht die Ableitung von sein kann: bei t = 0 ist die Steigung der Tangente größer als 1, der Wert von beträgt bei t = 0 aber 1.

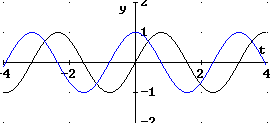
Die richtige Ableitung ergibt sich wie folgt:

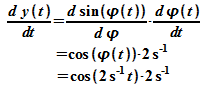
Dies Beispiel verdeutlicht die Kettenregel; sie lautet allgemein für verkettete Funktionen :

Kurze Merkregel in Worten: „äußere Ableitung mal innere Ableitung“.

Die Ableitungen von sind nach dieser Regel: