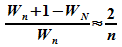3.4 Der lineare Potentialtopf
3.4.1 Unendlich hohe Wände
|
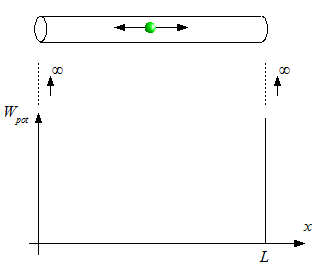
Ein Teilchen, z.B. ein Elektron, ist in einem lang gestreckten
Körper der Länge L eingeschlossen. Im Innern des
Körpers kann
sich das Teilchen frei bewegen. Die potentielle Energie ist also
konstant, und ihr Wert kann auf Wpot = 0
festgelegt werden.
Weiter soll das Teilchen nicht in die Begrenzungen des
Körpers
eindringen können, d.h. Wpot wird dort
unendlich groß.
Der Verlauf der potentiellen Energie hat also die Form eines
(unendlich hohen) Topfes, daher die Bezeichnung des Modells als linearer
Potentialtopf.
|
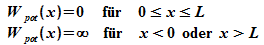
|
In
der Quantenmechanik wird das Teilchen durch eine Wellenfunktion
beschrieben, die der zeitunabhängigen Schrödinger-Gleichung
genügt. Im Außenraum besitzt die Schrödinger-Gleichung
nur die Lösung 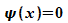 .
Damit die Wellenfunktion stetig ist, müssen die Lösungen im
Inneren die Randbedingungen
.
Damit die Wellenfunktion stetig ist, müssen die Lösungen im
Inneren die Randbedingungen
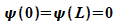
erfüllen.
Im Inneren lautet die Schrödinger-Gleichung:
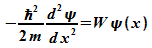
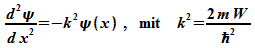
Die
allgemeine Lösung dieser Gleichung ist
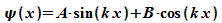
Die
Randbedingung für x = 0 ergibt
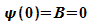
Die
Randbedingung für x = L
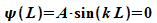
ist
erfüllt, wenn für die Wellenzahl k gilt 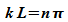 .
Es sind also nur bestimmte Werte für k erlaubt:
.
Es sind also nur bestimmte Werte für k erlaubt:
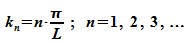
Für
jeden Wert von n existiert eine Wellenfunktion:
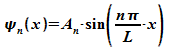
Diese
Funktionen werden als Eigenfunktionen bezeichnet. Da die
Energie mit der Wellenzahl über 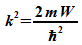 zusammenhängt, kann W nur die Werte
zusammenhängt, kann W nur die Werte
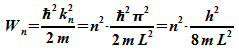
annehmen.
Die Energie ist also quantisiert:
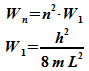
Diese
Werte werden als Eigenwerte der Energie bezeichnet. W1
ist die Grundzustandsenergie.Die Zahl n heißt
Quantenzahl der Energie. Der niedrigste mögliche
Energie-Eigenwert ist von Null verschieden, und entspricht der schon
bei den Unbestimmtheitsrelationen erwähnten Nullpunktsenergie.
Die
Konstanten An in den Wellenfunktionen werden
durch die Normierungsbedingung bestimmt:
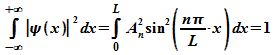
Mit
der Substitution:
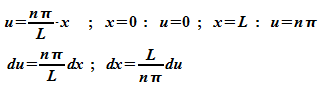
wird
die Normierungsbedingung zu
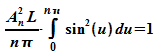
Das
Integral hat den Wert
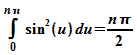
Damit
ergibt sich An zu
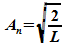
Die
normierten Eigenfunktionen für den linearen Potentialtopf (mit
unendlich hohen Wänden) lauten also:
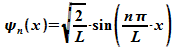
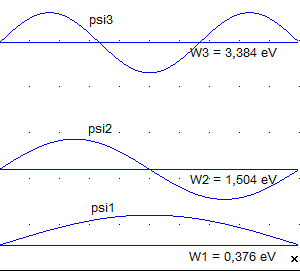
Für
ein Elektron in einem linearen Potentialtopf der Breite L = 1
nm sind die ersten drei Eigenwerte der Energie:
W1
= 0,376 eV ; W2 = 1,504 eV ; W3
= 3,384 eV
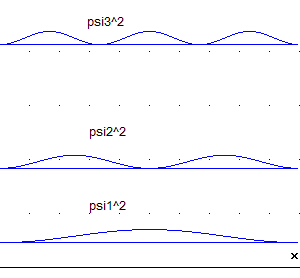
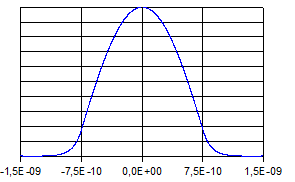
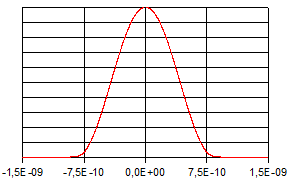
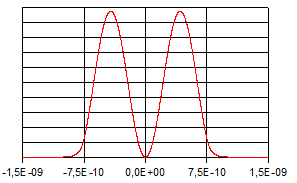
Die
folgenden Abbildungen zeigen die zugehörigen Graphen von 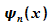 und
und 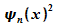 .
.
3.4.2 Endlich hohe Wände
Der
Fall des endlich hohen Potentialtopfes ist etwas komplizierter.
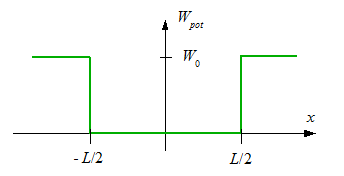
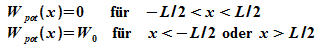
Für
ein Teilchen in diesem Potentialtopf ist W < W0.
Die
Schrödinger-Gleichung
lautet innen:
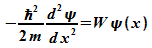
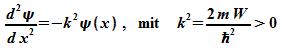
Daraus
ist abzulesen:
Außerhalb
des Potentialtopfes lautet die Schrödinger-Gleichung:
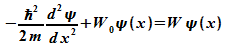
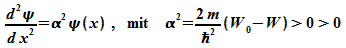
Hier
ist zu erkennen:
Wegen
dieses Krümmungsverhaltens divergiert die Wellenfunktion für
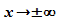 für die meisten Energiewerte.
Nur für ganz bestimmte
Energiewerte, die sogenannten Eigenwerte der Energie, werden
die physikalischen Randbedingungen
für die meisten Energiewerte.
Nur für ganz bestimmte
Energiewerte, die sogenannten Eigenwerte der Energie, werden
die physikalischen Randbedingungen 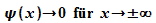 erfüllt. Die zugehörigen Wellenfunktionen werden als
Eigenfunktionen bezeichnet.
erfüllt. Die zugehörigen Wellenfunktionen werden als
Eigenfunktionen bezeichnet.
Die
Energie-Eigenwerte für ein Elektron in einem Potentialtopf der
Breite 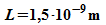 und der Höhe 4 eV sollen hier näherungsweise mit dem
Computer ermittelt werden.
und der Höhe 4 eV sollen hier näherungsweise mit dem
Computer ermittelt werden.
Die
zu lösende Schrödinger-Gleichung wird in folgender Form
geschrieben:
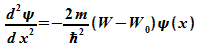
Daten:
|
Konstante der Schrödinger-Gleichung:
|
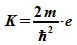
(Mit dem Faktor e werden die Energien
in eV erhalten.)
|
|
halbe Topfbreite:
|
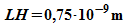
|
|
Schrittweite:
|
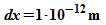
|
|
Startwerte:
|
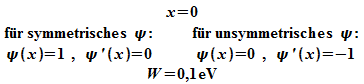
|
Rechenschleife:

Diese
Schleife wird für einen festen Energiewert bis 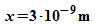 durchlaufen. Wenn sich außerhalb des Potentialtopfes nicht
durchlaufen. Wenn sich außerhalb des Potentialtopfes nicht 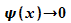 ergibt, wird der Energiewert verändert und die Schleife erneut
durchlaufen. Auf diese Weise werden schließlich die gesuchten
Eigenwerte der Energie gefunden.
ergibt, wird der Energiewert verändert und die Schleife erneut
durchlaufen. Auf diese Weise werden schließlich die gesuchten
Eigenwerte der Energie gefunden.
Es
gibt 5 Energie-Eigenwerte für das Elektron im Potentialtopf der
Höhe 4 eV:
W1
= 0,1311062 eV W2 = 0,522916 eV
W3
= 1,16626 eV
W4 = 2,0484 eV
W5
= 3,1176145 eV
Im
Vergleich dazu liegen die Energie-Eigenwerte im Potentialtopf mit
unendlich hohen Wänden 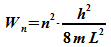 etwas höher:
etwas höher:
W1
= 0,167 eV W2
= 0,669 eV
W3 =
1,504 eV W4 = 2,674 eV
W5 =
4,175 eV
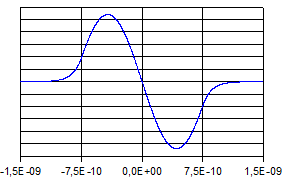
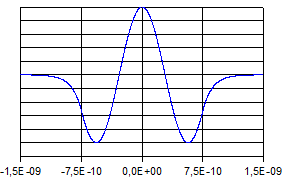
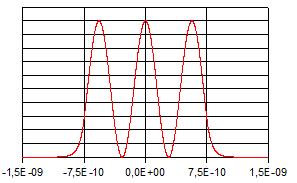
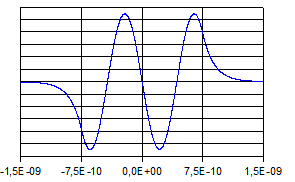
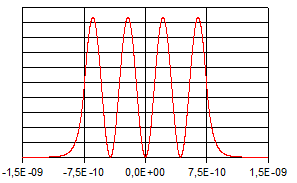
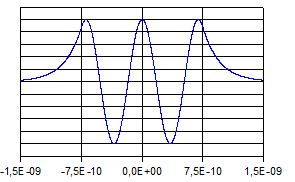
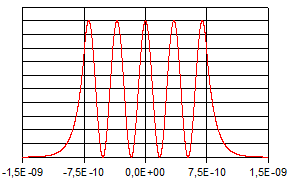
Die
folgenden Abbildungen zeigen die Verläufe der Eigenfunktionen
und der zugehörigen Aufenthaltswahrscheinlichkeitsdichten.
Übungen
1. Ein
Proton befinde sich in einem eindimensionalen Kasten der Länge
L. Berechnen Sie die Grundzutandsenergie für
a) 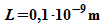 (Größenordnung eines Moleküls)
(Größenordnung eines Moleküls)
b) 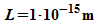 (Größenordnung eines Kerns).
(Größenordnung eines Kerns).
2. Ein
Körper der Masse 10-6 g bewege sich mit der
Geschwindigkeit 10-1 cm/s in einem Kasten der Länge
1 cm. Berechnen Sie den ungefähren Wert der Quantenzahl n.
3. a) Berechnen
Sie für den Körper aus 2a) die Orts- und
Impulsunbestimmtheit unter der Annahme 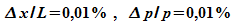
b) Welchen
Wert nimmt die Größe 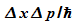 an?
an?
4. Zeigen
Sie, dass für große n die relative Differenz der
Energieniveaus im Potentialtopf mit unendlich hohen Wänden in
guter Näherung durch
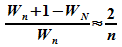
gegeben
ist.

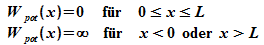
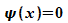 .
Damit die Wellenfunktion stetig ist, müssen die Lösungen im
Inneren die Randbedingungen
.
Damit die Wellenfunktion stetig ist, müssen die Lösungen im
Inneren die Randbedingungen 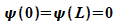
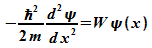
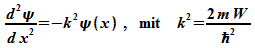
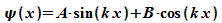
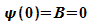
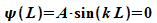
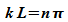 .
Es sind also nur bestimmte Werte für k erlaubt:
.
Es sind also nur bestimmte Werte für k erlaubt: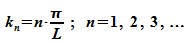
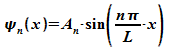
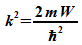 zusammenhängt, kann W nur die Werte
zusammenhängt, kann W nur die Werte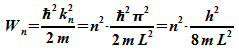
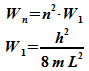
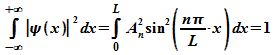
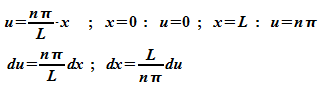
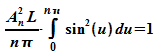
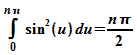
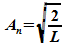
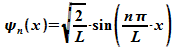
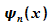 und
und 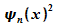 .
.

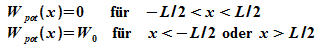
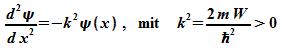
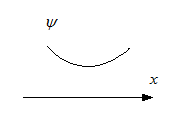
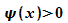 , dann ist
, dann ist 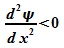 , der Graph von
, der Graph von 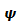 ist also rechtsgekrümmt.
ist also rechtsgekrümmt.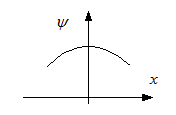
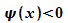 , dann ist
, dann ist 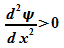 , der Graph von
, der Graph von 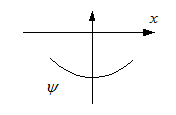
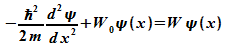
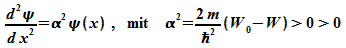
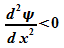 , der Graph von
, der Graph von 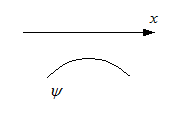
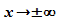 für die meisten Energiewerte.
Nur für ganz bestimmte
Energiewerte, die sogenannten Eigenwerte der Energie, werden
die physikalischen Randbedingungen
für die meisten Energiewerte.
Nur für ganz bestimmte
Energiewerte, die sogenannten Eigenwerte der Energie, werden
die physikalischen Randbedingungen 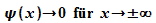 erfüllt. Die zugehörigen Wellenfunktionen werden als
Eigenfunktionen bezeichnet.
erfüllt. Die zugehörigen Wellenfunktionen werden als
Eigenfunktionen bezeichnet.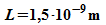 und der Höhe 4 eV sollen hier näherungsweise mit dem
Computer ermittelt werden.
und der Höhe 4 eV sollen hier näherungsweise mit dem
Computer ermittelt werden.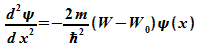
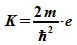
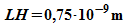
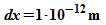
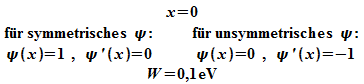

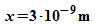 durchlaufen. Wenn sich außerhalb des Potentialtopfes nicht
durchlaufen. Wenn sich außerhalb des Potentialtopfes nicht 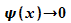 ergibt, wird der Energiewert verändert und die Schleife erneut
durchlaufen. Auf diese Weise werden schließlich die gesuchten
Eigenwerte der Energie gefunden.
ergibt, wird der Energiewert verändert und die Schleife erneut
durchlaufen. Auf diese Weise werden schließlich die gesuchten
Eigenwerte der Energie gefunden. 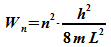 etwas höher:
etwas höher: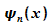
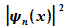
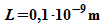 (Größenordnung eines Moleküls)
(Größenordnung eines Moleküls)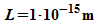 (Größenordnung eines Kerns).
(Größenordnung eines Kerns).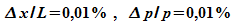
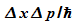 an?
an?