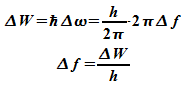3.2 Wellenfunktionen und Wellenpakete
Materielle
Objekte
wie
Elektronen, Protonen, Neutronen, Atome und Moleküle
zeigen Interferenzeffekte: Unter bestimmten Umständen zeigen
diese Objekte, die üblich als Teilchen angesprochen
werden, Welleneigenschaften. Entsprechend gilt für Wellen
wie z.B. elektromagnetische Strahlung, dass sie unter bestimmten
Umständen Teilcheneigenschaften zeigen, die mit dem
Konzept der Photonen beschrieben werden.
Nun
sind
Welle
und Teilchen sich gegenseitig ausschließende
Begriffe. Objekte wie Elektronen oder Photonen sind nicht
gleichzeitig Teilchen und Welle. Sie sind etwas anderes, das mit
klassisch-anschaulichen Begriffen nicht beschrieben werden kann. Sie
werden daher als Quantenobjekte bezeichnet.
Die
mathematische
Beschreibung
von Quantenobjekten erfolgt mit
Wellenfunktionen 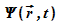 .
Ihre Amplitude ist eine Wahrscheinlichkeitsamplitude. Das
Betragsquadrat gibt die Wahrscheinlichkeitsdichte dafür an, ein
Quantenobjekt aus einer einheitlich präparierten Gesamtheit am
jeweiligen Ort zu registrieren
(Aufenthaltswahrscheinlichkeitsdichte):
.
Ihre Amplitude ist eine Wahrscheinlichkeitsamplitude. Das
Betragsquadrat gibt die Wahrscheinlichkeitsdichte dafür an, ein
Quantenobjekt aus einer einheitlich präparierten Gesamtheit am
jeweiligen Ort zu registrieren
(Aufenthaltswahrscheinlichkeitsdichte):

3.2.1 Klassische
Wellengleichung
Die
Differentialgleichung
einer
eindimensionalen Welle
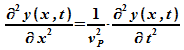
hat
harmonische
Wellen
alsLösungen:
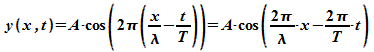
Übliche
Abkürzungen
sind:
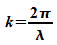 :
Wellenzahl
:
Wellenzahl
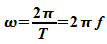 :
Kreisfrequenz
:
Kreisfrequenz
 :
Phase
:
Phase
Die
Phasengeschwindigkeit
ist
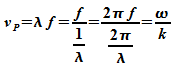
Anstelle
der
reellen
harmonischen Wellenfunktion y (x,t)
wird oft die komplexwertige Wellenfunktion
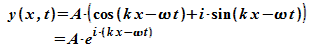
verwendet.
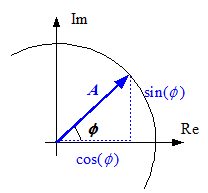
Dies
stellt
in der komplexen Zahlenebene einen Zeiger dar, der mit  rotiert:
rotiert:
3.2.2 Wellenpakete
Für
ein
Teilchen
mit Impuls p und Energie W ergeben sich
Wellenzahl k und Kreisfrequenz 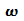 unter Verwendung der de Broglie-Beziehungen:
unter Verwendung der de Broglie-Beziehungen:
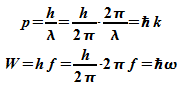

Damit
kann
eine
ebene Welle gebildet werden:
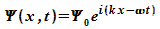
Diese
ebene
Welle
ist räumlich und zeitlich unendlich ausgedehnt, und
ihr Betragsquadrat ergibt:
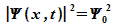
Das
bedeutet:
Beschreibt
man ein Teilchen mit der Wellenfunktion einer
ebenen Welle, dann ist das Teilchen zu jedem Zeitpunkt an jedem Ort
mit gleicher Wahrscheinlichkeit zu registrieren. Das Teilchen ist
also nicht lokalisiert.
Zur
Beschreibung
eines
lokalisierten Teilchens reicht eine einzelne
harmonische Welle also nicht aus. Dazu müssen mehrere Wellen
überlagert werden.
Überlagerung
zweier
harmonischer
Wellen
Ein
Elektron,
dass
sich mit  bewegt, hat den Impuls
bewegt, hat den Impuls
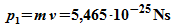
und
die
Energie

Daraus
ergeben
sich
Wellenzahl und Kreisfrequenz für eine harmonische
Welle:
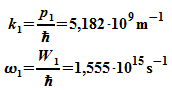
Für
eine
zweite
harmonische Welle wird gewählt:
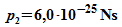
Dieser
Impuls
führt
zu
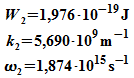
Aus
den
beiden
Wellen wird die Resultierende gebildet:

Es
genügt, den Realteil zu betrachten:
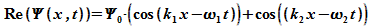
Unter
Berücksichtigung
von
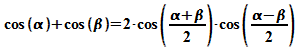
wird
daraus:
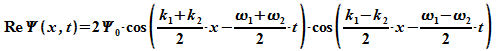
Zur
Abkürzung
werden
die Mittelwerte
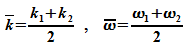
und
die
Differenzen
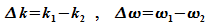
gebildet.
Die
Resultierende
nimmt dann die Form an
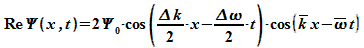
Dies
beschreibt
eine
harmonische Welle mit Wellenzahl 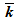 und Kreisfrequenz
und Kreisfrequenz  und einer modulierten Amplitude
und einer modulierten Amplitude 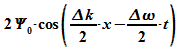 .
.
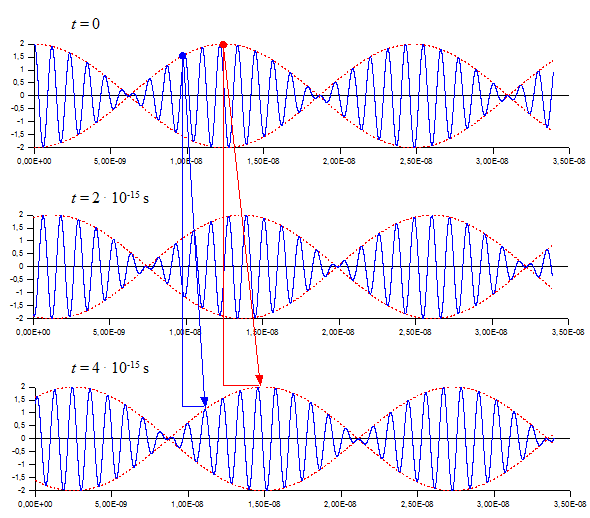
Beobachtung
1:
Die
resultierende
Welle
breitet sich mit der Phasengeschwindigkeit

aus.
Die
Einhüllende
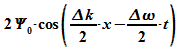 dagegen breitet sich mit der sogenannten Gruppengeschwindigkeit
dagegen breitet sich mit der sogenannten Gruppengeschwindigkeit
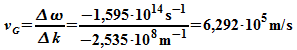
aus.
Es
ist
festzustellen:
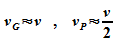
Die
Gruppengeschwindigkeit
stimmt
näherungsweise mit der
Teilchengeschwindigkeit überein, die Phasengeschwindigkeit ist
nur etwa halb so groß. In der Grafik sind zur Verdeutlichung
die Ausbreitung eines Maximums der Einhüllenden (rot) und die
Ausbreitung einer Phase der Welle (blau) markiert.
Beobachtung
2:
Die
Entfernung
von
2 Nullstellen der Einhüllenden 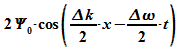 wird als Maß für die räumliche Ausdehnung des
Wellenpakets aufgefasst. Für zwei aufeinanderfolgende
Nullstellen gilt:
wird als Maß für die räumliche Ausdehnung des
Wellenpakets aufgefasst. Für zwei aufeinanderfolgende
Nullstellen gilt:
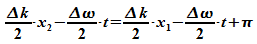
Zusammengefasst:
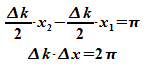
Mit
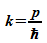 wird daraus
wird daraus
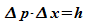
Für
einen
festen
Ort ergibt sich dasselbe Bild wie oben, jedoch für
die zeitliche Entwicklung, d.h. es ist x durch t zu
ersetzen. Für die zeitliche Ausdehnung des Wellenpaktes ergibt
sich
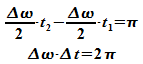
Mit
der
de
Broglie-Beziehung 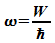 wird daraus
wird daraus
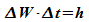
Kontinuierliche
Wellenpakete
Auch
das
aus
zwei harmonischen Wellen zusammengesetzte Wellenpaket ist zur
Beschreibung eines Teilchens noch nicht ausreichend: Außerhalb
der Bereiche 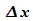 und
und 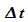 geht die Aufenthaltswahrscheinlichkeit nicht gegen Null.
geht die Aufenthaltswahrscheinlichkeit nicht gegen Null.
Ein
allgemeineres
Wellenpaket
erhält man aus der Überlagerung
mehrerer harmonischer Wellen:
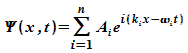
Aber
auch
mit
diesem Ansatz ergibt sich keine Wellenfunktion, die
außerhalb eines bestimmten Bereiches überall verschwindet.
Dies wird erst erreicht mit einem kontinuierlichen Wellenpaket:
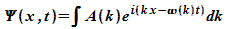
Dabei
ist
A(k) die Verteilungsfunktion der Wellenzahlen k.
Bei einem Gauß-Paket ist diese Verteilungsfunktion
gegeben durch
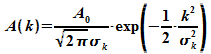
Die
Größe
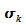 ist die sogenannte Standardverteilung. Sie ist mit
der
Breite der
Verteilung verknüpft.
ist die sogenannte Standardverteilung. Sie ist mit
der
Breite der
Verteilung verknüpft.
Die
sich
für
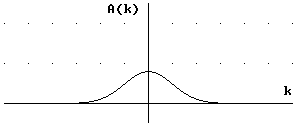
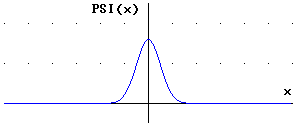
Gauß-Pakete ergebenden Wellenfunktionen 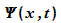 sind ebenfalls Gauß-Pakete. In den folgenden Abbildungen sind
verschieden breite Verteilungen A(k) und die dazu
gehörigen Anfangsverteilungen
sind ebenfalls Gauß-Pakete. In den folgenden Abbildungen sind
verschieden breite Verteilungen A(k) und die dazu
gehörigen Anfangsverteilungen 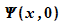 dargestellt.
dargestellt.
Es
ist zu erkennen: Zu einer schmalen Verteilung A(k) der
Wellenzahlen ergibt sich eine breite Anfangsverteilung 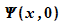 .
Ist die Verteilung der Wellenzahlen dagegen breit, ist die
Anfangsverteilung der Wellenfunktion schmal.
.
Ist die Verteilung der Wellenzahlen dagegen breit, ist die
Anfangsverteilung der Wellenfunktion schmal.
3.2.3 Phasengeschwindigkeit
und Gruppengeschwindigkeit
Für
eine
kontinuierliche
Verteilung harmonischer Wellen in einem
Wellenpaket 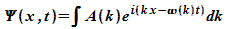 nimmt die Gruppengeschwindigkeit die Form
nimmt die Gruppengeschwindigkeit die Form
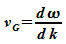
an.
Für
ein
freies Teilchen gilt
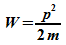
Mit
den
de
Broglie-Beziehungen 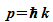 und
und  folgt daraus
folgt daraus
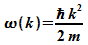
Damit
lässt
sich
die Gruppengeschwindigkeit berechnen:

Die
Gruppengeschwindigkeit
des
Wellenpaketes stimmt also mit der
Teilchengeschwindigkeit überein. Das war auch zu erwarten, denn
vG ist nichts anderes als die
Geschwindigkeit, mit der sich die Einhüllende des Pakets
ausbreitet und damit auch die Aufenthaltswahrscheinlichkeitsdichte
des Teilchens. Die Phasengeschwindigkeit vP
der einzelnen Wellen stimmt dagegen nicht mit der
Teilchengeschwindigkeit überein:
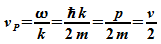
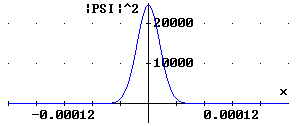
Dies
hat
zur
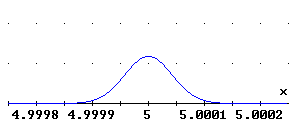
Folge, dass ein Wellenpaket mit der Zeit immer breiter wird:
es zerfließt. Dieses Zerfließen ist in den
folgenden Abbildungen für ein Elektron mit der Geschwindigkeit 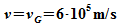 dargestellt.
dargestellt.
3.2.4 Wellenpakete und
Unbestimmtheitsrelation
Im
Folgenden soll die Bedeutung der Standardabweichungen 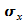 und
und 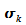 untersucht werden. Dazu werden Hilfsmittel aus der Stochastik
benötigt:
untersucht werden. Dazu werden Hilfsmittel aus der Stochastik
benötigt:
|
Eine Messreihe aus n Einzelmessungen xi
wird durch folgende statistische Größen beschrieben:
|
|
Mittelwert
|
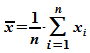
|
|
Varianz
|
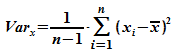
|
|
Standardabweichung
|
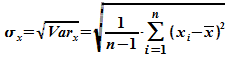
|
(1)
Nimmt
man
an einer Reihe identischer, d.h. durch dieselbe
Wellenfunktion  eine Ortsmessung vor, dann ist die Verteilung der in der Messung
bestimmten Orte durch die Aufenthaltswahrscheinlichkeitsdichte
eine Ortsmessung vor, dann ist die Verteilung der in der Messung
bestimmten Orte durch die Aufenthaltswahrscheinlichkeitsdichte  gegeben. Für die Messung der Orte eines Teilchens besteht also
eine Unbestimmtheit, die mit der räumlichen Ausdehnung des
Wellenpaketes verknüpft ist. Die räumliche Ausdehnung des
Wellenpakets steht ihrerseits mit der Verteilung A(k)
der Wellenzahlen im Wellenpaket im Zusammenhang.
gegeben. Für die Messung der Orte eines Teilchens besteht also
eine Unbestimmtheit, die mit der räumlichen Ausdehnung des
Wellenpaketes verknüpft ist. Die räumliche Ausdehnung des
Wellenpakets steht ihrerseits mit der Verteilung A(k)
der Wellenzahlen im Wellenpaket im Zusammenhang.
(2)
Ist
die
räumliche Ausdehnung des Wellenpakets sehr gering, liegt
also ein räumlich schmales Wellenpaket vor, so ergibt sich eine
breite Verteilung der Wellenzahlen. Die zum Aufbau des Wellenpaketes
benötigten Wellenzahlen streuen sehr weit. Da die Wellenzahl k
über 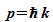 mit dem Impuls zusammenhängt, ergibt sich auch eine entsprechend
hohe Impulsunbestimmtheit. Umgekehrt: Liegt ein räumlich breites
Wellenpaket vor, also eine hohe Unbestimmtheit in der Messung des
Ortes, so ist die Verteilung A(k) schmal und die
Unbestimmtheit in der Messung des Impulses ist gering.
mit dem Impuls zusammenhängt, ergibt sich auch eine entsprechend
hohe Impulsunbestimmtheit. Umgekehrt: Liegt ein räumlich breites
Wellenpaket vor, also eine hohe Unbestimmtheit in der Messung des
Ortes, so ist die Verteilung A(k) schmal und die
Unbestimmtheit in der Messung des Impulses ist gering.
(3)
Nach
diesen
Überlegungen ist es sinnvoll, die Orts- und
Impulsunbestimmtheit genauer zu definieren, nämlich als die
Standardabweichungen der Verteilungen bei der Messung des Ortes und
des Impulses:
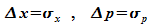
Heisenberg
zeigte,
dass
für Gauß-Pakete das Produkt 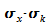 den Wert 1/2 annimmt, und für jede andere Verteilung
größer
als 1/2 ist:
den Wert 1/2 annimmt, und für jede andere Verteilung
größer
als 1/2 ist:
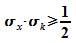
Da
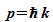 ist, ist auch
ist, ist auch 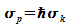 ,
und es folgt
,
und es folgt
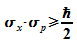
Damit
ergibt
sich
die exakte Formulierung der Heisenberg'schen
Unbestimmtheitsrelation:
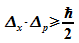
3.2.5 Unbestimmtheitsrelation
für Energie und Zeit
Für
einen
festen
Zeitpunkt t0 hängt die räumliche
Verteilung eines Wellenpaketes 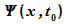 mit der Verteilung A(k) der Wellenzahlen zusammen.
Betrachtet man dagegen einen festen Ort x0, dann
ergibt sich ein gleicher Zusammenhang zwischen der zeitlichen
Verteilung
mit der Verteilung A(k) der Wellenzahlen zusammen.
Betrachtet man dagegen einen festen Ort x0, dann
ergibt sich ein gleicher Zusammenhang zwischen der zeitlichen
Verteilung 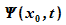 des Wellenpaketes mit der Verteilung der Kreisfrequenzen
des Wellenpaketes mit der Verteilung der Kreisfrequenzen  .
Die Kreisfrequenz hängt mit der Energie zusammen:
.
Die Kreisfrequenz hängt mit der Energie zusammen: 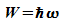 .
Ein zeitlich schmales Wellenpaket bedingt daher eine breite
Verteilung der Energie, ein zeitlich breites Wellenpaket bedingt eine
schmale Verteilung der Energie. In Analogie zur
Unbestimmtheitsrelation von Ort und Impuls wird deshalb eine Relation
für die Zeit- und Energieumbestimmtheit formuliert:
.
Ein zeitlich schmales Wellenpaket bedingt daher eine breite
Verteilung der Energie, ein zeitlich breites Wellenpaket bedingt eine
schmale Verteilung der Energie. In Analogie zur
Unbestimmtheitsrelation von Ort und Impuls wird deshalb eine Relation
für die Zeit- und Energieumbestimmtheit formuliert:
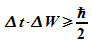
Diese
Relation
ist
wie folgt zu interpretieren: Wenn 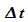 die für eine Energiemessung eines Teilchens zur Verfügung
stehende Zeit ist, dann ist diese mit der als Standardabweichung
definierten Unbestimmtheit der Energie
die für eine Energiemessung eines Teilchens zur Verfügung
stehende Zeit ist, dann ist diese mit der als Standardabweichung
definierten Unbestimmtheit der Energie 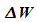 verknüpft.
verknüpft.
Auch
für
Zerfälle
angeregter und instabiler Zustände
besitzt die Zeit-Energie-Unbestimmtheitsrelation eine große
Bedeutung. In diesem Fall entspricht 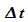 der mittleren Lebensdauer
der mittleren Lebensdauer 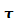 des Zustands und
des Zustands und 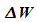 der Unbestimmtheit der bei dem Zerfall frei werdenden Energie. Dies
bedingt auch die natürliche Linienbreite von Spektrallinien
angeregter Atome:
der Unbestimmtheit der bei dem Zerfall frei werdenden Energie. Dies
bedingt auch die natürliche Linienbreite von Spektrallinien
angeregter Atome:
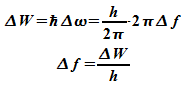
Übungen
1.
Ein
Proton bewege sich mit  .
.
a)
Berechnen
Sie Impuls p1, Energie W1,
Wellenzahl k1 und Kreisfrequenz w1.
b)
Um
ein Wellenpaket aus zwei harmonischen Wellen zu bilden, wird eine
zweite Welle mit dem Impuls p2 = 1,1 p1
verwendet. Berechen Sie die zugehörigen Werte W2,
k2, w2.
c)
Ermitteln
Sie die Gruppen- und Phasengeschwindigkeit des Wellenpakets.
2.
Begründen
Sie: Zu
einer schmalen Verteilung A(k) der Wellenzahlen ergibt
sich eine breite Anfangsverteilung 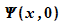 .
Ist die Verteilung der Wellenzahlen dagegen breit, ist die
Anfangsverteilung der Wellenfunktion schmal.
.
Ist die Verteilung der Wellenzahlen dagegen breit, ist die
Anfangsverteilung der Wellenfunktion schmal.
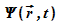 .
Ihre Amplitude ist eine Wahrscheinlichkeitsamplitude. Das
Betragsquadrat gibt die Wahrscheinlichkeitsdichte dafür an, ein
Quantenobjekt aus einer einheitlich präparierten Gesamtheit am
jeweiligen Ort zu registrieren
(Aufenthaltswahrscheinlichkeitsdichte):
.
Ihre Amplitude ist eine Wahrscheinlichkeitsamplitude. Das
Betragsquadrat gibt die Wahrscheinlichkeitsdichte dafür an, ein
Quantenobjekt aus einer einheitlich präparierten Gesamtheit am
jeweiligen Ort zu registrieren
(Aufenthaltswahrscheinlichkeitsdichte):
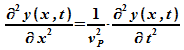
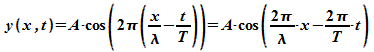
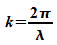 :
Wellenzahl
:
Wellenzahl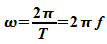 :
Kreisfrequenz
:
Kreisfrequenz :
Phase
:
Phase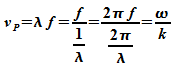
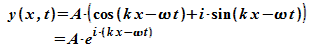

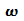 unter Verwendung der de Broglie-Beziehungen:
unter Verwendung der de Broglie-Beziehungen: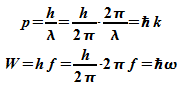

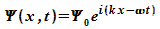
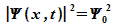
 bewegt, hat den Impuls
bewegt, hat den Impuls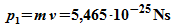

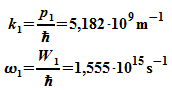
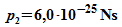
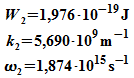

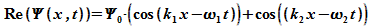
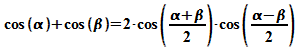
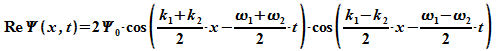
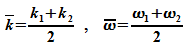
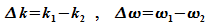
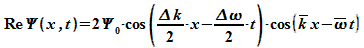
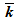 und Kreisfrequenz
und Kreisfrequenz  und einer modulierten Amplitude
und einer modulierten Amplitude 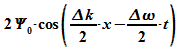 .
.


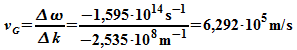
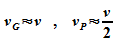
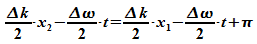
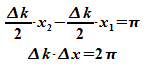
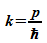 wird daraus
wird daraus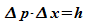
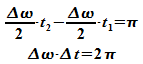
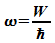 wird daraus
wird daraus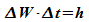
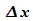 und
und 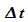 geht die Aufenthaltswahrscheinlichkeit nicht gegen Null.
geht die Aufenthaltswahrscheinlichkeit nicht gegen Null.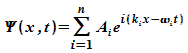
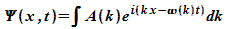
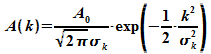
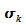 ist die sogenannte Standardverteilung. Sie ist mit
der
Breite der
Verteilung verknüpft.
ist die sogenannte Standardverteilung. Sie ist mit
der
Breite der
Verteilung verknüpft.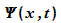 sind ebenfalls Gauß-Pakete. In den folgenden Abbildungen sind
verschieden breite Verteilungen A(k) und die dazu
gehörigen Anfangsverteilungen
sind ebenfalls Gauß-Pakete. In den folgenden Abbildungen sind
verschieden breite Verteilungen A(k) und die dazu
gehörigen Anfangsverteilungen 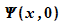 dargestellt.
dargestellt.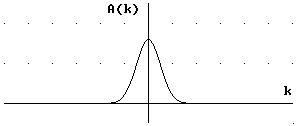



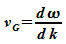
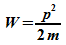
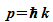 und
und  folgt daraus
folgt daraus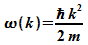

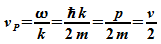
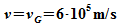 dargestellt.
dargestellt.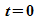

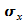 und
und 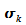 untersucht werden. Dazu werden Hilfsmittel aus der Stochastik
benötigt:
untersucht werden. Dazu werden Hilfsmittel aus der Stochastik
benötigt: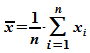
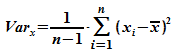
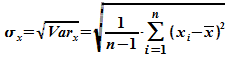
 eine Ortsmessung vor, dann ist die Verteilung der in der Messung
bestimmten Orte durch die Aufenthaltswahrscheinlichkeitsdichte
eine Ortsmessung vor, dann ist die Verteilung der in der Messung
bestimmten Orte durch die Aufenthaltswahrscheinlichkeitsdichte  gegeben. Für die Messung der Orte eines Teilchens besteht also
eine Unbestimmtheit, die mit der räumlichen Ausdehnung des
Wellenpaketes verknüpft ist. Die räumliche Ausdehnung des
Wellenpakets steht ihrerseits mit der Verteilung A(k)
der Wellenzahlen im Wellenpaket im Zusammenhang.
gegeben. Für die Messung der Orte eines Teilchens besteht also
eine Unbestimmtheit, die mit der räumlichen Ausdehnung des
Wellenpaketes verknüpft ist. Die räumliche Ausdehnung des
Wellenpakets steht ihrerseits mit der Verteilung A(k)
der Wellenzahlen im Wellenpaket im Zusammenhang.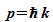 mit dem Impuls zusammenhängt, ergibt sich auch eine entsprechend
hohe Impulsunbestimmtheit. Umgekehrt: Liegt ein räumlich breites
Wellenpaket vor, also eine hohe Unbestimmtheit in der Messung des
Ortes, so ist die Verteilung A(k) schmal und die
Unbestimmtheit in der Messung des Impulses ist gering.
mit dem Impuls zusammenhängt, ergibt sich auch eine entsprechend
hohe Impulsunbestimmtheit. Umgekehrt: Liegt ein räumlich breites
Wellenpaket vor, also eine hohe Unbestimmtheit in der Messung des
Ortes, so ist die Verteilung A(k) schmal und die
Unbestimmtheit in der Messung des Impulses ist gering.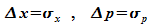
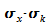 den Wert 1/2 annimmt, und für jede andere Verteilung
größer
als 1/2 ist:
den Wert 1/2 annimmt, und für jede andere Verteilung
größer
als 1/2 ist: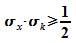
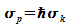 ,
und es folgt
,
und es folgt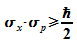
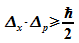
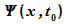 mit der Verteilung A(k) der Wellenzahlen zusammen.
Betrachtet man dagegen einen festen Ort x0, dann
ergibt sich ein gleicher Zusammenhang zwischen der zeitlichen
Verteilung
mit der Verteilung A(k) der Wellenzahlen zusammen.
Betrachtet man dagegen einen festen Ort x0, dann
ergibt sich ein gleicher Zusammenhang zwischen der zeitlichen
Verteilung 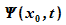 des Wellenpaketes mit der Verteilung der Kreisfrequenzen
des Wellenpaketes mit der Verteilung der Kreisfrequenzen  .
Die Kreisfrequenz hängt mit der Energie zusammen:
.
Die Kreisfrequenz hängt mit der Energie zusammen: 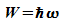 .
Ein zeitlich schmales Wellenpaket bedingt daher eine breite
Verteilung der Energie, ein zeitlich breites Wellenpaket bedingt eine
schmale Verteilung der Energie. In Analogie zur
Unbestimmtheitsrelation von Ort und Impuls wird deshalb eine Relation
für die Zeit- und Energieumbestimmtheit formuliert:
.
Ein zeitlich schmales Wellenpaket bedingt daher eine breite
Verteilung der Energie, ein zeitlich breites Wellenpaket bedingt eine
schmale Verteilung der Energie. In Analogie zur
Unbestimmtheitsrelation von Ort und Impuls wird deshalb eine Relation
für die Zeit- und Energieumbestimmtheit formuliert: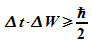
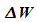 verknüpft.
verknüpft.
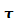 des Zustands und
des Zustands und