3. Quantenmechanik

3.1 Unbestimmtheitsrelationen

3.1.1 Formulierung der Unbestimmtheitsrelationen

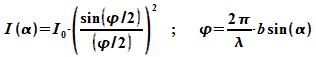
Werden Wellen an einem Spalt der Breite b gebeugt, so ergibt sich die Intensitätsverteilung

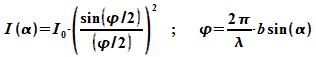
Die Minima ergeben sich aus 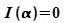. Diese Bedingung ist erfüllt wenn 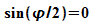ist, also

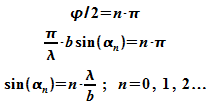
Als Beispiel wird hier Licht der Wellenlänge 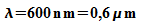betrachtet, das an Spalten unterschiedlicher Breite b gebeugt wird:

Wie beim Doppelspaltversuch baut sich auch beim Einzelspalt für Licht und Elektronen die Verteilung der Lokalisationen stochastisch auf und wird nach hinreichend langer Zeit durch die Intensitätsverteilung 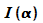beschrieben.

Werner Heisenberg (Nobelpreis 1932) untersuchte 1926 das Verhalten von Elektronen am Spalt mit folgender Überlegung:

Um diesen Mittelwert abzuschätzen nahm Heisenberg den Betrag 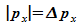an, der klassische Teilchen zum ersten Minimum unter dem Winkel 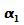führen würde:

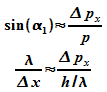
Es folgt also:

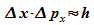
Das bedeutet: Der Versuch, den Ort von Elektronen durch Verkleinerung der Spaltbreite genauer zu bestimmen, führt zu einer Vergrößerung der Unbestimmtheit, mit der man den Impuls der Elektronen kennt. Umgekehrt gilt: Wenn der Impuls genauer bestimmt werden soll, dann muss die Spaltbreite und damit die Unbestimmtheit des Ortes vergrößert werden. Ort und Impuls können nicht gleichzeitig beliebig genau bestimmt werden.

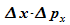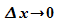Das Produkt kann also nie Null werden. Der Versuch, den Ort scharf zu bestimmen () führt zu völliger Unbestimmtheit des Impulses (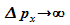). Umgekehrt führt der Versuch einer scharfen Impulsbestimmung (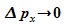) zu völliger Unbestimmtheit im Ort ().

3.1.2 Erste Anwendungen der Unbestimmtheitsrelationen

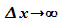1. Teilchenbahnen

Eine direkte Folge der Unbestimmtheitsrelation ist, dass es im Bereich atomarer Größenordnungen keine Bahnen von Teilchen mehr gibt. Für klassische Teilchen kann die Bewegung mit der Bahnkurve 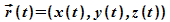und der Geschwindigkeit 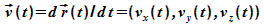bzw dem Impuls 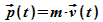beschrieben werden. Dabei werden Ort und Impuls gleichzeitig exakt angegeben, was bei Quantenobjekten jedoch nicht mehr möglich ist. Als Beispiel werden eine Gewehrkugel und ein Elektron betrachtet, die sich mit 500 m/s bewegen:

Dies Beispiel verdeutlicht: Für makroskopische Körper wie die Gewehrkugel ist die Unbestimmtheit der Geschwindigkeit unmessbar klein, so dass es gerechtfertigt ist, sie in der klassischen Mechanik zu vernachlässigen. Bei Quantenobjekten ist sie dagegen so groß, dass der Begriff der Bahn jeden Sinn verliert.

2. Nullpunktsenergie

Eine wichtige Konsequenz der Heisenberg'schen Unbestimmtheitsrelationen ist die Existenz der sogenannten Nullpunktsenergie (auch: Lokalisationsenergie), die ein Quantenobjekt immer dann besitzt, wenn es in einem bestimmten Raumbereich eingeschlossen ist. Beispiel: Ein Elektron sei in einem eindimensionalen Bereich der Länge L eingeschlossen. Seine Unbestimmtheit im Ort ist dann 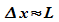. Aus der Unbestimmtheitsrelation ergibt sich für die Unbestimmtheit im Impuls:

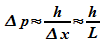
Die Impulse des Elektrons liegen zwischen 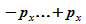, also ist 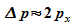, und es folgt

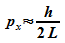
Für die kinetische Energie des Elektrons ergibt sich damit

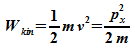
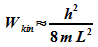
Bei dreidimensionalen Problemen ist mit 3 zu multiplizieren:

Für Abschätzungen wird auch die Form

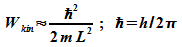
verwendet.

Die Nullpunktsenergie besitzen Teilchen auch am absoluten Temperaturnullpunkt T = 0. Bei Verkleinerung des Raumbereiches, in dem ein Teilchen eingeschlossen ist, wächst diese Energie stark an. Beim sogenannten Beta-Zerfall radioaktiver Elemente wird beobachtet, dass die zerfallenden Atomkerne Elektronen aussenden. Zu Beginn der Untersuchungen dieser Vorgänge wurde angenommen, dass der Atomkern also Elektronen enthalte. Nun sind Kerne von der Größenordnung 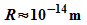, und die Elektronen hätten dann eine Nullpunktsenergie von etwa

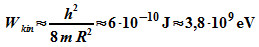
Die gemessenen Energien von Elektronen aus dem Beta-Zerfall liegen aber nur in der Größenordnung bis 1 MeV. Somit können die Elektronen nicht schon vor dem Zerfall im Kern vorhanden gewesen sein.

3. Größe und Grundzustandsenergie des Wasserstoffatoms

Das Elektron im Wasserstoffatom bewegt sich im Feld des Protons. Es besitzt daher kinetische Energie und potentielle Energie:

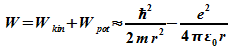
Die minimale Energie ergibt sich aus :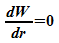

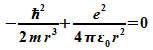
Für die Größe des H-Atoms folgt damit der sogenannte Bohr-Radius:

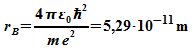
Die Energie des Elektrons im Grundzustand ergibt sich für den Bohr-Radius:

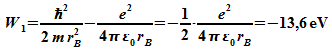
Dies ist in Übereinstimmung mit der gemessenen Ionisierungsenergie des H-Atoms.

4. Chemische Energie

Chemische Prozesse spielen sich in der Atomhülle ab. Hier liegen typische Energien bei etwa 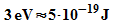pro Atom. In 1 mol befinden sich 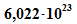Atome, so dass sich die chemische Energie von etwa 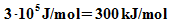ergibt. Beispiel: Kohlenstoff hat einen Heizwert von 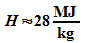. Für Kohlenstoff gilt 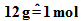, also 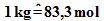. Damit wird der Heizwert 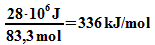, was zu der Abschätzung passt.

5. Kerne

Die Protonen in den Kernen sind in einem Bereich der Größenordnung 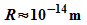eingeschlossen. Mit der Protonenmasse 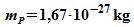ergibt sich die Abschätzung der Nullpunktsenergie

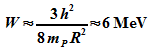
Dies ist die Größenordnung der Energien von 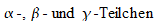, die bei radioaktiven Prozessen den Kern verlassen.

Übungen