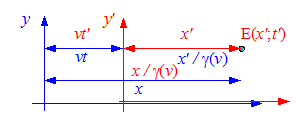
Ereignisse E(x;t) haben in relativ zueinander gleichförmig bewegten Inertialsystemen unterschiedliche Raum-Zeit-Koordinaten. In einem Minkowski-Diagramm können diese Koordinaten durch Projektion auf die Koordinatenachsen bestimmt werden. Hier soll nun ein rechnerisches Verfahren zur Transformation der Raum-Zeit-Koordinaten von einem Inertialsystem in ein anderes entwickelt werden.
Dazu wird folgende Anordnung betrachtet. Relativ zu einem Inertialsystem S bewegt sich ein zweites Inertialsystem S' mit der Geschwindigkeit v in positiver x-Richtung. Zum Zeitpunkt t = t' = 0 passieren sich die beiden Koordinatenursprünge. Zu einer späteren Zeit t' wird am Ort x' in S' ein Lichtsignal ausgelöst. Dies ist das Ereignis E(x'; t'). Welche Koordinaten hat das Ereignis im System S?
|
System |
System S' |
|---|---|
|
Direkt abzulesen ist |
|
|
|
|
|
Daraus ergibt sich, wie ein Beobachter |
|
|
in S |
in S' |
|
aus den von ihm registrierten Koordinaten |
|
|
(x; t) |
(x'; t') |
|
die Raumkoordinate |
|
|
in S' |
in S |
|
berechnet: |
|
|
|
|
|
Einsetzen der Transformationsgleichung für die Raum-Koordinate x bzw. x' ergibt |
|
|
|
|
|
Die Transformationsgleichungen für die Zeit-Koordinaten lauten also |
|
|
|
|
Beispiel: In einem System S' sind zwei Ereignisse mit den Koordinaten E1(2 Ls; 2s) und E2(6 LS ; 5 s) gegeben. Relativ zu S bewegt sich ein System S' mit konstanter Geschwindigkeit v = 0,6 c in x-Richtung. Die Koordinaten der Ereignisse in S' ergeben sich durch die Gleichungen der Lorentz-Transformation.
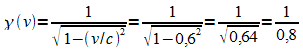
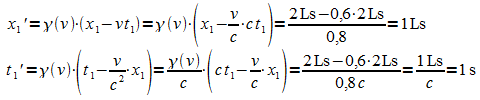
Im Bereich von Geschwindigkeiten, die klein gegen die Lichtgeschwindigkeit sind, können Geschwindigkeiten einfach addiert werden. Zwei Fahrzeuge, die sich mit v1 = 50 km/h nach rechts bzw. mit v2 = 70 km/h nach links bewegen, haben eine Relativgeschwindigkeit von vrel = v1 + v2 = 120 km/h. Im Bereich relativistischer Geschwindigkeiten ist diese einfache Addition nicht mehr richtig: Zwei sich mit v1 = 0,5 c nach rechts bzw. mit v2 = 0,7 c nach links fliegende Raketen haben nicht die Relativgeschwindigkeit 0,5 c + 0,7 c = 1,2 c. Hier muss also ein anderes Gesetz zur Addition von Geschwindigkeiten gelten.
Zur Herleitung des Additionsgesetzes wird folgende Anordnung betrachtet. Relativ zu einem Inertialsystem S bewegt sich ein zweites Inertialsystem S' mit der Geschwindigkeit v in positiver x-Richtung. Zum Zeitpunkt t = t' = 0 passieren sich die beiden Koordinatenursprünge. Im System S' bewegt sich ein Körper gleichförmig mit den Geschwindigkeitskomponenten u' = x' / t' und w' = y' / t'.
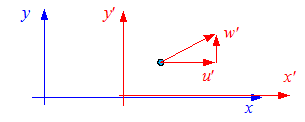
Mit den Gleichungen der Lorentz-Transformation
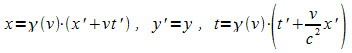
ergibt sich:
|
|
|
|
Die Gleichungen der umgekehrten Transformation ergeben sich, indem v durch –v ersetzt wird: |
|
|
|
|
Beispiel 1: Es werden die beiden oben genannten Raketen betrachtet. In Bezug auf ein Inertialsystem S – z.B. eine Beobachtungsstation auf der Erde – bewegen sich die beiden Raketen mit v1 = 0,5 c und v2 = –0,7 c. Die mit den Raketen verbundenen Inertialsysteme seien S' bzw. S''. In S wird folgende Zuordnung vorgenommen:
Rakete 1 wird als das System S' betrachtet, das sich mit v = v1 = 0,5 c nach rechts bewegt;
Rakete 2 wird als der sich mit u = v2 = –0,7 c bewegende Körper betrachtet.
Dann ergibt sich in S' die Geschwindigkeit von Rakete 2 zu
.
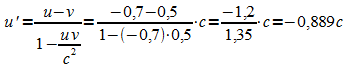Ein Beobachter in Rakete 1 sieht also Rakete 2 mit der Geschwindigkeit 0,889 c auf sich zu kommen.
Es kann aber auch folgende Zuordnung vorgenommen werden:
Rakete 2 wird als das System S' betrachtet, das sich mit v = v2 = –0,7 c nach links bewegt;
Rakete 1 wird als der sich mit u = v1 = 0,5 c bewegende Körper betrachtet.
Dann ergibt sich in S' die Geschwindigkeit von Rakete 1 zu
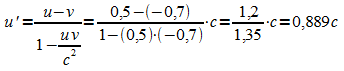
Ein Beobachter in Rakete 2 sieht also Rakete 1 mit der Geschwindigkeit 0,889 c auf sich zu kommen.
Beispiel 2: Das System S' bewege sich mit der Geschwindigkeit v relativ zum System S in x-Richtung. In S' breitet sich ein Lichtsignal mit u' = c in x'-Richtung aus. Die Geschwindigkeit u des Lichtsignals in S ist dann
.
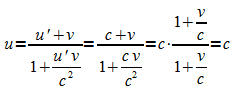Wenn sich das Lichtsignal in S' in y'-Richtung ausbreitet, dann ist u' = 0 und w' = c. In S ergeben sich dann die Geschwindigkeitskomponenten
.
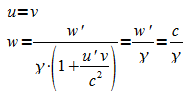Der Betrag der Geschwindigkeit des Lichtsignals in S ist
.
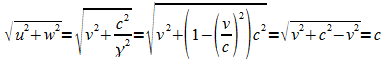Längen und Zeitintervalle sind relative Größen: zwei inertiale Beobachter erhalten im allgemeinen verschiedene Werte für diese Größen. Es stellt sich die Frage, ob es irgend etwas gibt, worin zwei verschiedene Beobachter übereinstimmen. Dies ist der Fall: bekannt ist schon, dass beide dieselbe Lichtgeschwindigkeit und dieselben Längen senkrecht zur Relativbewegung messen.
Es sei wieder S' ein Inertialsystem, das sich relativ zu einem zweiten (ruhenden) Inertialsystem S mit der Geschwindigkeit v in x-Richtung bewegt. Zu einer fundamentalen Beziehung gelangt man ausgehend von der Zeitdilatation:
.
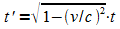Quadrieren und multiplizieren mit c2 ergibt
.
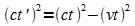Das Produkt vt ist die Strecke L, die das bewegte System für einen Beobachter in S in der Zeit t zurückgelegt hat. Ein Beobachter, der in S' ruht, hat dagegen in S' die Strecke L' = 0 zurückgelegt. Damit folgt
.
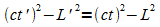Die Differenz aus den Quadraten der Orts- und Zeitkoordinaten wird also von beiden Beobachtern gleich ermittelt.
Mit
der Lorentz-Transformation lässt sich dieser Zusammenhang noch
verallgemeinern. Für zwei Ereignisse E1(x1;
t1) und E2(x2; t2)
in
einem
Inertialsystem
S
ist
der
räumliche Abstand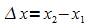 
und der zeitliche Abstand 
.
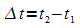Im relativ zu S mit der Geschwindigkeit v in x-Richtung
bewegten Inertialsystem S' ergeben sich die Abstände 
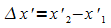und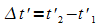 
.
Die Lorentz-Transformation ergibt den Zusammenhang der Abstände
in beiden Systemen:
.
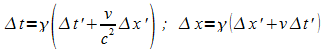Damit folgt weiter:
Die
Größe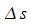 
mit
,
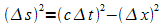wird als Raum-Zeit-Intervall bezeichnet. In Worten:
(Raum-Zeit-Intervall)2 = (c * zeitlicher Abstand)2 – (räumlicher Abstand)2 .
Diese Größe hat in allen Inertialsystemen den gleichen Wert. Das Raum-Zeit-Intervall ist daher eine invariante (oder absolute) Größe. Allgemeiner ist unter Berücksichtigung der drei Raumdimensionen
.
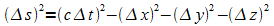Beispiele:
Es sei immer v /c = 3/5 = 0,6; dann ist g= 5/4 = 1,25.
|
1) E1(2 Ls; 2 Ls), E2(4 Ls; 5 Ls)
|
|
|
|
|
|
3) E1(2 Ls; 2 Ls), E2(6 Ls; 5 Ls)
|
|
Übungen
1. Leiten Sie mit den Lorentz-Transformationsgleichungen die Formel für die Zeitdilatation her. Legen Sie zunächst zwei Ereignisse für die Ablesung einer in S bewegten, in S' ruhenden Uhr fest. Beachten Sie, dass die Ablesung in S' am gleichen Ort (x'1 = x'2), in S an verschiedenen Orten erfolgt.
2. Ein radioaktiver Kern fliegt mit v = 0,5 c und sendet in seinem Ruhsystem Elektronen mit einer Geschwindigkeit von 0,6 c aus. Welche Geschwindigkeiten haben die Elektronen in und entgegen der Flugrichtung des Kerns im Laborsystem?
Lösungen
1. –
2. u1
= 0,846 c (in Flugrichtung des Kerns) ;
u2
= –0,143 c (entgegen der Flugrichtung des Kerns)
