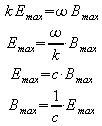Zunächst wird das Entstehen der Induktionsspannung
in einer Leiterschleife betrachtet. Bei Zunahme der Flussdichte ![]() gilt nach
dem Lenz'schen Gesetz: Der Induktionsstrom Iind muss
(in technischer Richtung) so fließen, dass das von ihm erzeugte
Magnetfeld B(Iind) der Zunahme von B
entgegenwirkt.
gilt nach
dem Lenz'schen Gesetz: Der Induktionsstrom Iind muss
(in technischer Richtung) so fließen, dass das von ihm erzeugte
Magnetfeld B(Iind) der Zunahme von B
entgegenwirkt.
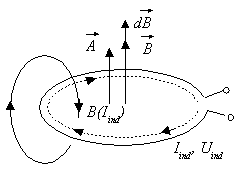
Als Antrieb für den Induktionsstrom wurde bisher stets die Induktionsspannnung betrachtet:
![]() .
.
Eine Spannung entsteht aber in einem elektrischen Feld. Das Auftreten eines Induktionsstroms kann also auf das Entstehen einer induzierten elektrischen Feldstärke zurückgeführt werden.
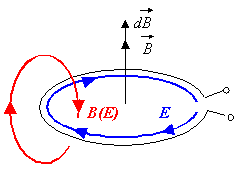
Tatsächlich wird die Leiterschleife nur zum Nachweis der Induktionserscheinung benötigt. Das elektrische Feld entsteht auch ohne Leiterschleife und bildet einen Wirbel um das Magnetfeld, dessen zeitliche Veränderung die Ursache für das elektrische Feld ist. Es wird daher als ein Wirbelfeld bezeichnet.
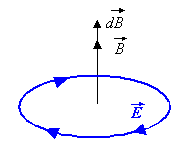
In der Elektrostatik dagegen – also bei zeitlich konstanten elektrischen Feldern – beginnen die Feldlinien an positiven Ladungen und enden an negativen Ladungen. Hier ist die elektrische Ladung die Quelle des Feldes, und das elektrostatische Feld ist ein so genanntes Quellenfeld.
Das elektrische Wirbelfeld lässt sich experimentell nachweisen, indem um eine Glaskugel mit Neon-Füllung eine Ringspule gelegt wird. Mit dieser Spule wird ein hochfrequentes, zeitveränderliches Magnetfeld erzeugt, das die Glaskugel durchsetzt. Dabei wird eine ringförmige Leuchterscheinung sichtbar. Diese entsteht dadurch, dass das elektrische Feld die Gasmoleküle ionisiert. Der leuchtende Ring demonstriert also die geschlossenen elektrischen Feldlinien.

Das Induktionsgesetz soll nun so umformuliert werden, dass anstelle der Spannung die eigentliche ursächliche Größe, also die elektrische Feldstärke, erscheint. Im homogenen Feld eines Plattenkondensators hängen Spannung und Feldstärke zusammen über die einfache Beziehung
![]() .
.
In inhomogenen Feldern gilt für die Spannung zwischen zwei Feldpunkten allgemeiner:
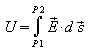 .
.
Für das elektrische Wirbelfeld ist ein vollständiger,
geschlossener Umlauf zu wählen. Wird noch berücksichtigt,
dass der magnetische Fluss ![]() ist, ergibt sich die
ist, ergibt sich die
|
2. Maxwell-Gleichung:
(James Clerk Maxwell. 1831-1879) In Worten: Ein sich zeitlich änderndes Magnetfeld ist von einem elektrischen Wirbelfeld umschlossen. |
|
Rechenbeispiel: Es wird eine schlanke, zylindrische Feldspule betrachtet, die von einem sinusförmigen Wechselstrom durchflossen wird. Die Daten sind:
![]() .
.
Für die zeitabhängige Flussdichte im Spuleninnern ergibt sich damit
![]() .
.
Im Innern der Feldpule wird eine ringförmige Leiterschleife mit dem Radius rR = 12 cm so angebracht, dass ihre Fläche vom Magnetfeld senkrecht durchsetzt wird. Die 2. Maxwell-Gleichung wird für einen vollständigen Umlauf längs der Leiterschleife ausgewertet:
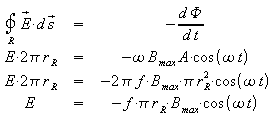
Die Amplitude der induzierten Feldstärke ist also
![]() .
.
|
f / Hz |
102 |
103 |
106 |
|
Emax / (V/m) |
0,0148 |
0,148 |
148 |
|
Uind / V |
0,0112 |
0,112 |
112 |
Ein elektrischer Strom erzeugt ein Magnetfeld, wie schon Oersted 1820 entdeckte. Für die Flussdichte im Abstand r von einem geraden, vom Strom I durchflossenen Leiter gilt
![]() .
.
Bewegt man eine kleine Magnetnadel einmal um den stromführenden Leiter herum, hat sich die Nadel einmal gedreht. Es ist also Arbeit an ihr verrichtet worden.
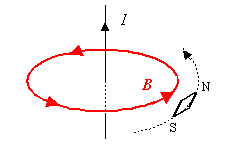
Eine plausible Annahme ist, dass die verrichtete Arbeit proportional zur Flussdichte B ist. Dann ergibt sich für die Arbeit
![]() .
.
Der Vektor der Flussdichte verläuft stets tangential zu den kreisförmigen Feldlinien des Magnetfeldes:
|
|
|
Für einen vollen Umlauf auf einer kreisförmigen Feldlinie folgt für das Wegintegral der Flussdichte:
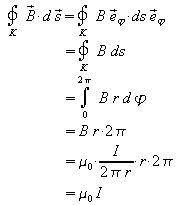
Die Beziehung
![]()
heißt Durchflutungssatz (oder Ampere'scher Satz des Magnetfeldes).
Beim Aufladen eines Kondensators fließt ein Ladungsstrom IL im Leiterkreis. Dieser Ladungsstrom erregt ein magnetisches Feld. Zwischen den Platten fließt kein Ladungsstrom, aber es baut sich ein elektrisches Feld auf. Maxwells Annahme war nun, dass auch zwischen den Platten ein magnetisches Wirbelfeld existiert, solange das elektrische Feld aufgebaut wird - gewissermaßen als Fortsetzung des vom Ladungsstrom erzeugten Magnetfelds um die Leiter.
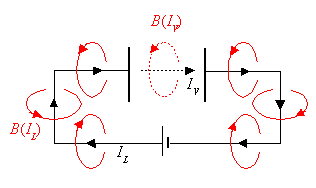
Das Magnetfeld zwischen den Platten führte Maxwell auf einen Verschiebungsstrom zurück. Dieser Strom transportiert zwar keine Ladung, erzeugt aber auch ein magnetisches Feld. Beim Plattenkondensator ergibt sich dieser Verschiebungsstrom wie folgt.
Für die Ladung auf dem Kondensator gilt zu jedem Zeitpunkt
![]() .
.
Der Verschiebungsstrom ist die zeitliche Veränderung der Plattenladung:
![]() .
.
Wenn der Vektor der elektrischen Feldstärke und der Flächennormalenvektor einen von Null verschiedenen Winkel einschließen, ergibt sich etwas allgemeiner:
![]() .
.
Wird der Verschiebungsstrom im Durchflutungssatz berücksichtigt, so erhält man
![]() .
.
Wenn kein Ladungsstrom, sondern nur ein sich zeitlich veränderndes elektrisches Feld vorhanden ist, ergibt sich die
|
1. Maxwell-Gleichung:
In Worten: Ein sich zeitlich änderndes elektrisches Feld ist von einem magnetischen Wirbelfeld umschlossen. |
|
Rechenbeispiel: Ein ebener Plattenkondensator mit kreisförmigen Platten wird an eine sinusförmige Wechselspannung angeschlossen. Die Daten sind:
![]() .
.
Für die zeitabhängige elektrische Feldstärke im Kondensator gilt damit:
![]() .
.
Für einen kreisförmigen Umlauf mit Radius r = 12 cm um das Feld im Kondensatorinneren liefert die 1. Maxwell-Gleichung:
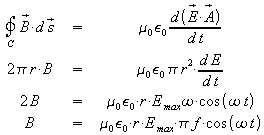
Die Amplitude der magnetischen Flussdichte ist also
![]() .
.
|
f / Hz |
103 |
106 |
109 |
|
Bmax / T |
|
|
|
Die 1. und die 2. Maxwell-Gleichung beschreiben das magnetische bzw. das elektrische Wirbelfeld und den Zusammenhang dieser beiden Felder. In der oben angegebenen Formulierung ist jeweils vorausgesetzt, dass ein homogenes Feld eine ebene Fläche durchsetzt. Eine Verallgemeinerung ergibt sich daher, wenn inhomogene elektrische und magnetische Felder betrachtet werden, die beliebige, gekrümmte Flächen im Raum durchsetzen.

Die gekrümmte Fläche A sei von einer geschlossenen
Linie C berandet. A wird in kleine Flächenelemente ![]() zerlegt, die
näherungsweise eben und so klein sind, dass die
Feldgröße
zerlegt, die
näherungsweise eben und so klein sind, dass die
Feldgröße ![]() auf diesem Flächenelement als konstant betrachtet
werden kann. Der gesamte Fluss ergibt sich dann näherungsweise
durch die Summe
auf diesem Flächenelement als konstant betrachtet
werden kann. Der gesamte Fluss ergibt sich dann näherungsweise
durch die Summe
![]() .
.
Im Grenzwert ![]() werden daraus so genannte Flächenintegrale:
werden daraus so genannte Flächenintegrale:
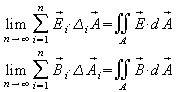
Die Maxwell-Gleichungen lauten damit:
|
1. Maxwell-Gleichung: 2. Maxwell-Gleichung: |
Zur vollständigen Beschreibung elektrischer und magnetischer Felder werden noch Beziehungen zwischen den Feldern und ihren Quellen benötigt. Die 3. Maxwell-Gleichung bringt die Tatsache zum Ausdruck, dass elektrische Ladungen die Quellen elektrischer Felder sind, während die 4. Maxwell-Gleichung besagt, dass es keine magnetischen Ladungen als Quellen magnetischer Felder gibt. Magnetfelder sind stets Wirbelfelder.
|
3. Maxwell-Gleichung: 4. Maxwell-Gleichung: |
Die Kraftwirkung der Felder auf Ladungen wird in der Gleichung für die Lorentzkraft beschrieben:
![]() .
.
Mit diesem Satz von Gleichungen können im Prinzip alle elektromagnetischen Vorgänge im Vakuum beschrieben werden.
Nun ist aber auch das sich zeitlich ändernde magnetische Feld seinerseits von einem sich zeitlich ändernden elektrischen Wirbelfeld umschlossen. Dieses wiederum wird von einem sich zeitlich ändernden Magnetfeld umschlossen, das von einem elektrischen Wirbelfeld umschlossen wird usw.
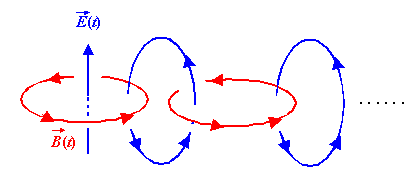
Dies führte Maxwell 1868 zu der Voraussage:
Ein sich zeitlich änderndes elektromagnetisches Feld breitet sich im Raum als elektro-magnetische Welle aus.
Wie die Skizze vermuten lässt, stehen elektrisches und magnetisches Feld stets senkrecht aufeinander.
Wegen der Energieerhaltung müssen elektrische und magnetische Energiedichte gleich sein:
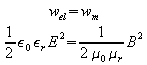
Daraus folgt:
![]()
Im Vakuum ist ![]() , und
, und
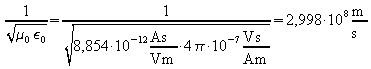 .
.
Dies ist die Vakuumlichtgeschwindigkeit c. Es kann daher angenommen werden, dass sich elektromagnetische Wellen mit Lichtgeschwindigkeit ausbreiten.
In Materie gilt nach diesen Überlegungen:
![]() .
.
Für nicht-ferromagnetische Stoffe ist ![]() , so dass die
Lichtgeschwindigkeit in Materie von den dielektrischen Eigenschaften
des Mediums abhängt:
, so dass die
Lichtgeschwindigkeit in Materie von den dielektrischen Eigenschaften
des Mediums abhängt:
![]() .
.
Aus der ersten Maxwell-Gleichung
und der zweiten Maxwell-Gleichung
ergibt sich eine einfache Herleitung der Ausbreitung elektromagnetischer Wellen im Raum. Zur Vereinfachung der Rechnung werden folgende Voraussetzungen gemacht:
1) die elektrische Feldstärke habe nur eine y-Komponente,
die sich in x-Richtung ändert;
2) die magnetische Flussdichte habe nur eine z-Komponente.
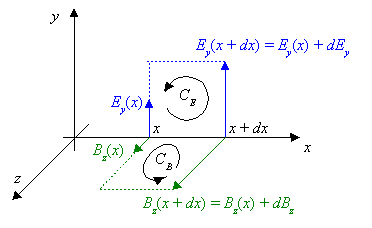
1. Zur Auswertung der 2. Maxwell-Gleichung wird der Rand CE des in der xy-Ebene liegenden Rechtecks gewählt:
![]() .
.
Das Magnetfeld steht senkrecht auf der Rechteckfläche, so dass gilt:
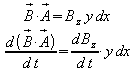 .
.
Es folgt also
![]() ,
,
und damit
![]() .
.
Zur Auswertung der 1. Maxwell-Gleichung wird der Rand CB des in der xz-Ebene liegenden Rechtecks gewählt.
![]() .
.
Das elektrische Feld steht senkrecht auf der Rechteckfläche, so dass gilt:
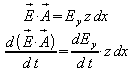 .
.
Einsetzen in die 1. Maxwell-Gleichung führt auf
![]() ,
,
woraus folgt
![]() .
.
2. Gleichung (1) wird nun nach x abgeleitet:
![]()
und Gleichung (2) wird nach t abgeleitet:
![]() .
.
Ohne Beweis sei mitgeteilt, dass die Reihenfolge der Ableitungen von Bz nach x und nach t vertauscht werden darf. Der Vergleich von (3) und (4) zeigt dann:
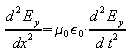 (5).
(5).
Dies stimmt mit der Differentialgleichung einer eindimensionalen Welle überein:
![]() .
.
Die Rechnung zeigt also:
1) Die elektrische Feldstärke Ey(x,t) genügt der Differentialgleichung der Wellenausbreitung;
2) die Phasengeschwindigkeit ist ![]() .
.
3. Um zu Aussagen über das Magnetfeld zu kommen wird entsprechend vorgegangen. Ableiten von Gleichung (1) nach t und Ableiten von Gleichung (2) nach x ergibt:
![]()
![]()
Da auch hier die Reihenfolge der Ableitungen nach x und t vertauscht werden darf, führen die Gleichungen (6) und (7) auf
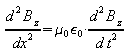 (8)
(8)
Das bedeutet:
1) Das Magnetfeld Bz(x,t) genügt der Differentialgleichung der Wellenausbreitung;
2) die Phasengeschwindigkeit ist ![]() .
.
4. Eine Lösung von Gleichung (5) ist die eindimensionale harmonische Welle:
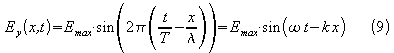
mit der Kreisfrequenz ![]() und der Wellenzahl
und der Wellenzahl ![]() .
.
Eine Lösung der Wellengleichung (8) für das Magnetfeld ist entsprechend
![]()
Nach Gleichung (1) ist ![]() . Werden Gleichung (9) nach x
und Gleichung (10) nach t abgeleitet, so ergibt sich aus dieser
Gleichheit:
. Werden Gleichung (9) nach x
und Gleichung (10) nach t abgeleitet, so ergibt sich aus dieser
Gleichheit:
![]() ,
,
also