3. Berechnung der Lorentz-Kraft

ausgeübt, wenn die Stromrichtung senkrecht zum Magnetfeld steht. Der Strom besteht in metallsichen Leitern aus bewegten Elektronen, so dass man fragen kann, wie groß die auf ein einzelnes Elektron ausgeübte Kraft ist. ZurBerechnung dieser Kraft wird ein zylindrischer Leiter der Länge s betrachtet, der von einem Strom I durchflossen wird. Senkrecht zum Leiter wird ein homogenes Magnetfeld angelegt.

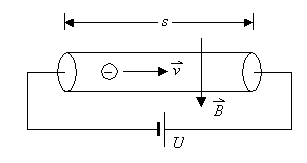
Der Strom wird von einer Anzahl N von Elektronen mit dem Ladungsbetrag Q = N e gebildet:

Die freien Elektronen im Leiter bewegen sich mit der konstanten Driftgeschwindigkeit v. Daher ist

Eingesetzt in I:

Da die Bewegungsrichtung der Elektronen und der Vektor der magnetischen Flussdichte senkrecht aufeinander stehen, gilt

Da N die Anzahl der freien Elektronen ist, kann der Ausdruck evB als die Kraft, die auf ein einzelnes Elektron wirkt, gedeutet werden. Also: Ein Elektron, das sich mit der Geschwindigkeit v senkrecht zu einem B-Feld bewegt, erfährt dort die Lorentz-Kraft

Wenn Bewegungsrichtung des Elektrons und Magnetfeldrichtung keinen rechten Winkel bilden, dann kann der Geschwindigkeitsvektor des Elektrons in zwei Komponenten zerlegt werden:

• eine Komponente v_P parallel (oder anti-parallel) zur Richtung des Magnetfeldes,
• eine Komponente v_S senkrecht zur Richtung des Magnetfeldes.

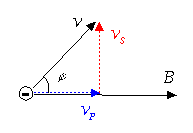
Die Lorentz-Kraft entsteht nur durch die Bewegung senkrecht zum Magnetfeld. Also gilt allgemeiner:

Die Richtung der Lorentz-Kraft ergibt sich nach der 3-Finger-Regel der linken Hand:
 

• Daumen   --> in Bewegungsrichtung v_S des Elektrons senkrecht zum Magnetfeld,
• Zeigefinger  -->  in Richtung des Magnetfeldes

dann zeigt der
• Mittelfinger -->  in Richtung der Lorentz-Kraft F_L.

Um die Richtung der Lorentz-Kraft zu bestimmen ist jetzt die 3-Finger-Regel der rechten Hand anzuwenden.

Übungen

1. Ein Elektron fliegt mit der Geschwindigkeitdurch ein homogenes Magnetfeld mit der magnetischen Flussdichte. Der von dem Geschwindigkeitsvektorund dem Vektor der magnetischen Flussdichteeingeschlossene Winkelbeträgt

a) 0°, b) 35°, c) 90°, d) 180°.

Der Betrag F der auf das Elektron wirkenden Kraft ist zu berechnen.

2. Ein Elektron fliegtdurch ein Magnetfeld. Das Magnetfeld hat am Ort des Elektrons die magnetische Flussdichte, das Elektron hat die Geschwindigkeit. Auf das Elektron wirkt die Lorentz-Kraft. Welcheen Winkel bildet der Geschwindigkeitsvektor des Elektrons mit dem Vektor B der magenetischen Flussdichte?

3. Das erdmagnetische Feld habe an einem Beobachtungsort die Flussdichte, der Vektorbilde mit der Horizontale den Winkel. Ein mit der LadunggeladenerRegentropfen hat die Masse m = 0,1 g; er erfährt beim Fallen im erdmagnetischen Feld die Lorentz-Kraft F_L.

a) Mit welcher Geschwindigkeit müsste der Regentropfen fallen, wenn die auftretende Lorentz-Kraft ein Millionstel der Gewichtskraft F_G des Tropfens betragen soll?

b) (*) Lesen Sie im Lehrbuch den Abschnitt „Fall mit Luftwiderstand“ nach. Berechnen Sie dann die Endgeschwindigkeit eines fallenden Regentropfens vom Radius r = 1 mm. Vergleichen Sie den erhaltenen Wert mit der in a) berechneten Geschwindigkeit. Spielt die Lorentz-Kraft beim Fall elektrisch geladener Regentropfen eine Rolle?

4. Ein Proton besitzt in einem senkrecht nach unten gerichteten Magnetfeld mit B = 40 T eine nach Westen gerichtete Geschwindigkeit von. Geben Sie Betrag und Richtung der wirkenden Kraft an.
 
 
 

Lösungen

1.

2.

3.

4.