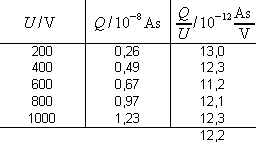
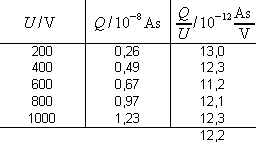
Entsprechend wurde im Abschnitt 2.3 bei der Untersuchung des homogenen Feldes ein Plattenkondensator geladen und die Ladung gemessen:
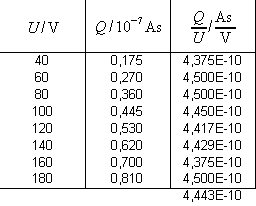
Anordnungen, die Ladung speichern können, werden als Kondensatoren bezeichnet. Die beiden Beispiele lassen vermuten, dass Ladung und Spannung proportional zueinander sind. Man definiert daher als Kapazität C eines Kondensators:
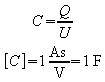
Die Einheit ist das Farad F (nach Michael Faraday). In der Praxis treten jedoch meist nur deutlich kleinere Kapazitäten auf. Bei technischen Kondensatoren finden sich die Größenordnungen
.
2. Für den Plattenkondensator mit Plattenfläche A und Plattenabstand d gilt
,
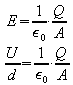woraus sich ablesen lässt:
.
Beispiel: Für kreisförmige Platten mit Radius r = 12,5 cm und Abstand d = 1 mm ergibt sich eine Kapazität von
.
3. Ein Kugelkondensator besteht aus zwei konzentrisch angeordneten Kugeln mit Innenradius ri und Außenradius ra. Wenn die innere Kugel gegenüber der äußeren Kugel positiv aufgeladen wird, dann gilt für die Spannung
.
Daraus ergibt sich die Kapazität
.
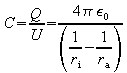Im Grenzwert 
erhält man die Kapazität einer frei stehenden Kugel mit Radius
R:
.
Beispiel: Für einen Kugelradius R = 5 cm ist die Kapazität der Kugel
.