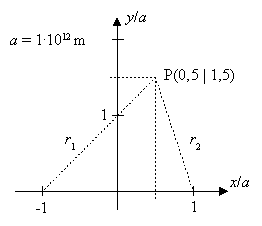![]()
Die beiden Sterne werden gemäß der nebenstehenden Abbildung symmetrisch in einem Koordinatensystem angeordnet.
In jedem Punkt des Raumes überlagern sich die Gravitationsfelder der beiden Massen. Die resultierende Feldstärke in einem Punkt P ergibt sich aus der vektoriellen Summe der Einzelfeldstärken:
![]() .
.
Die Beträge der Feldstärken in P sind:
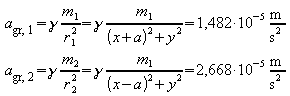
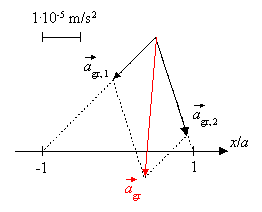
Damit kann die resultierende Feldstärke zeichnerisch ermittelt werden. Es ergibt sich
![]()