.
.
Soll er aus einer Höhe h1 in eine Höhe h2
gehoben werden, muss eine Hubarbeit verrichtet werden, die der Zunahme
an potentieller Energie entspricht:
.
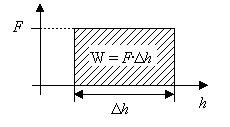
In einem Weg-Kraft-Diagramm entspricht diese Arbeit (bzw. Energie) der Fläche unter dem Weg-Kraft-Graphen.
Beim radialen Feld ist die aufzuwendende Kraft beim Heben eines Körpers von einem Anfangspunkt P0 zu einem Zielpunkt PZ nicht mehr konstant. Zunächst soll der Körper längs einer Feldlinie gehoben werden.Die Grundidee zur Berechnung der Arbeit als Fläche unterhalb des Weg-Kraft-Graphen ist dann folgende.
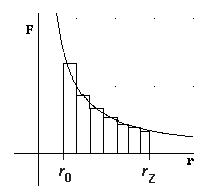
Der Abstand des Startpunktes vom Mittelpunkt des Zentralkörpers
ist
r0, der Abstand des Zielpunktes ist rZ.
Nun wird das Intervall von r0 bis rZ
in so kleine Teilbereiche der Breite
geteilt,
dass in diesen die Gravitationskraft näherungsweise als konstant betrachtet
werden kann. Die in einem solchen Teilintervall verrichtete Arbeit ist
dann ungefähr
,
was der Fläche eines Rechteckstreifens entspricht. Wenn n die
Anzahl solcher Rechteckstreifen ist, dann ergibt sich für die insgesamt
verrichtete Hubarbeit und damit für die Zunahme an potentieller Energie
.
Je schmaler die Rechteckstreifen gemacht werden, desto besser wird die
eigentlich gesuchte Fläche unter dem Weg-Kraft-Graphen angenähert.
Im Grenzfall für
,
oder (was dasselbe bedeutet)
ergibt
sich das Integral
Die zugeführte Energie und damit die Zunahme der potentiellen Energie ist also
.
|
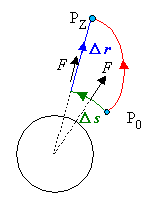
Wird der Körper längs eines beliebigen Weges gehoben, so kann der Weg in Teilstücke  in
Feldlinienrichtung und in Bogenstücke quer
dazu zerlegt werden. Auf diesen Querstücken stehen Kraft und Weg senkrecht
aufeinander, d.h. es wird keine Arbeit verrichtet. Da also nur die radialen
Wegstücke beitragen, ergibt sich wie oben
|
 |
Da die Gravitationskraft auf einen Probekörper im Feld eines Zentralkörpers
in sehr großer Entfernung („im Unendlichen“) Null wird, wird das
Nullniveau für die potentielle Energie ins Unendliche gelegt:
.
Um einen Körper vom Startpunkt P0 ins Unendliche zu heben,
ist also die Arbeit
nötig. Dies ist gleich der Differenz der potentiellen Energien:
.
Damit wird die potentielle Energie im Gravitationsfeld negativ:
.
.
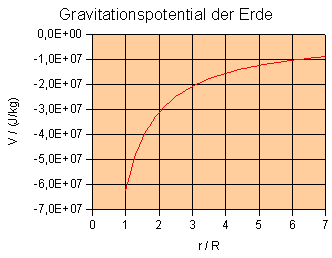
Darstellung des Gravitationspotentials der Erde:
Es sei R der Erdradius und M die Erdmasse. An der Erdoberfläche
ist
.
Damit lässt sich das Gravitationspotential schreiben als
.
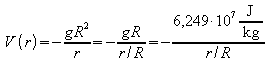Hubarbeit und Potentialdifferenz:
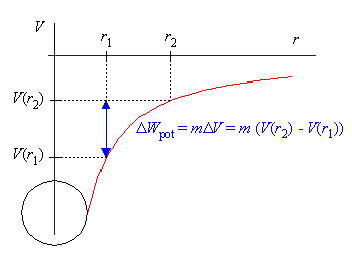
(M: Erdmasse; rE: Erdradius) zugeführt werden. Wird ihm diese Energie in Form von kinetischer Energie beim Abschuss von der Erdoberfläche zugeführt, dann gilt
.
Daraus ergibt sich die nötige Anfangsgeschwindigkeit, die als Fluchtgeschwindigkeit bezeichnet wird:
.
Die Fluchtgeschwindigkeit hängt nicht von der Masse des abgeschossenen Körpers ab, sondern nur von Masse und Radius der Erde. Für andere Himmelskörper gilt dieselbe Überlegung wie für die Erde, so dass die Fluchtgeschwindigkeit eine charakteristische Größe eines Himmelskörpers ist.
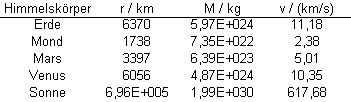
Die Fluchtgeschwindigkeit ist auch maßgeblich dafür, ob ein Planet eine Atmosphäre besitzen und wie dicht diese sein kann. Gasmoleküle, deren Geschwindigkeit größer als die Fluchtgeschwindigkeit ist, verlassen den Planeten.
.
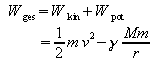Bei der Kreisbewegung gilt
.
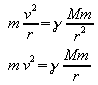Eingesetzt in die Beziehung für die Gesamtenergie:
.
Die Gesamtenergie ist also negativ:
.
Übungen
S.122, A2, A3, A4
Weitere Übungen
1. Die Schwerpunkte von zwei Schiffen, von denen jedes die Masse m = 20 000 t hat, haben den Abstand r = 100 m. Die Schiffe werden näherungsweise als Massenpunkte betrachtet. Wie groß ist die Kraft, mit der sie sich gegenseitig anziehen?
2. Eine Bleikugel (Masse m1) wird an einen
Arm einer Waage angehängt und austariert. Der Radius der Kugel ist
r1
= 1,0 cm. Vertikal unter diese erste Bleikugel wird eine zweite Bleikugel
(Masse m2) gelegt. Der Radius der zweiten Kugel ist r2
= 50 cm. Der Abstand zwischen den beiden Kugeloberflächen beträgt
s
= 1 cm.
Durch die Kugel 2 nimmt die Kraft zu, mit der die Kugel 1 an ihrer
Aufhängung zieht. Wieviel Prozent ihrer Gewichtskraft FG1
beträgt diese Zunahme? (Dichte von Blei: r
= 11,3 g/cm3)
3. a) Setzen Sie die Gewichtskraft eines Körpers an der Erdoberfläche der Gravitationskraft gleich und zeigen Sie so, dass gilt:
;
rE:
Erdradius, mE: Erdmasse
b) Berechnen Sie ohne Verwendung der Gravitationskonstante die Gewichtskraft eines Körpers der Masse m = 1 kg für die Höhe h = 100 km über der Erdoberfläche. (rE = 6370 km)
4. Ein Satellit kreist in der Äquatorebene um die Erde. Seine Umlaufzeit T stimmt mit der Umdrehungszeit der Erde überein. Berechnen Sie ohne Verwendung der Gravitationskonstante den Radius r der Kresibahn des Satelliten. (rE = 6370 km; T = 86 164 s)
5. Mit welcher Anfangsgeschwindigkeit v0 muss ein Körper von der Erdoberfläche vertikal nach oben geschossen werden, wenn er die Höhe h = rE = 6370 km erreichen soll? Rechnen Sie ohne Verwendung der Gravitationskonstante. Der Luftwiderstand soll vernachlässigt werden.
6. Ein Körper der Masse m = 1 kg soll von der Oberfläche
der ruhend zu denkenden Erde in eine Höhe h = 400 km gebracht
werden. Berechnen Sie die aufzuwendende Arbeit ohne Verwendung der Gravitationskonstante
a) unter der vereinfachenden Annahme, dass die Gravitationskraft konstant
ist,
b) unter Berücksichtigung der Tatsache, dass die Gravitationskraft
mit der Höhe abnimmt.
c) Um wieviel Prozent weicht der wahre Wert vom Näherungswert
ab?
(rE = 6370 km)
7. Welche Arbeit ist erforderlich, um einen Körper der Masse
m
= 1 kg von der Erdoberfläche aus dem Anziehungsbeeich der Erde zu
entfernen? Mit welcher Geschwindigkeit müsste der Körper abgeschossen
werden, um ihm diese Arbeit als kinetische Energie mitzugeben?
(
)
8. a) Wieviel Prozent vom Gravitationspotential der Erde beträgt
das Gravitationspotential des Mondes an der Erdoberfläche?
(mE = 81 mM ; Abstand Erdmittelpunkt
– Mondmittelpunkt: d = 60 rE ; rE:
Erdradius)
b) Wieviel Prozent vom Gravitationspotential des Mondes beträgt
das Gravitationspotential der Erde an der Mondoberfläche?
(Abstand Erdmittelpunkt – Mondmittelpunkt: d = 220 rM
; rM: Mondradius)
9. Ein Satellit bewegt sich auf einer Kreisbahn um die Erde.
Sein Abstand von der Erdoberfläche ist h = 10 000 km.
a) Wie groß ist die Bahngeschwindigkeit v des Satelliten?
b) Berechnen Sie die Umlaufzeit des Satelliten.
Lösungen
1. 2,67 N
2. 
3. b) FG = 9,51 N
4. r = 42 100 km
5. Energieerhaltung führt auf 
6. a) W1 = 3,92 MJ
b) W2 = 3,69 MJ
c) DW = 5,91%
7.
v = 11,2 km/s
8. a) 0,02%
b) 37%
9. a) v = 4,94 km/s
b) T = 348 min
.