3. Das Newton'sche Gravitationsgesetz

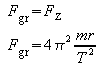
Das Gravitationsgesetz soll hier unter folgenden vereinfachenden Voraussetzungen hergeleitet werden:

1. Die Trabantenbahn ist eine Kreisbahn.

2. Die Masse M des Zentralkörpers ist sehr groß gegen die Masse m des Trabanten, so dass die Schwerpunktbewegung des Systems vernachlässigt werden kann. Anders ausgedrückt: der Zentralkörper befindet sich in Ruhe.

Die Gravitationskraft ist die Zentripetalkraft der Kreisbewegung:

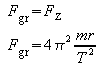
Erweitern mit r² führt auf

C ist die Konstante aus dem 3. Kepler-Gesetz. Es lässt sich erkennen, dass die Gravitationskraft proportional zur Masse m des Trabanten und umgekehrt proportional zum Quadrat des Bahnradius ist. Anders formuliert: Die Gravitationskraft nimmt quadratisch mit dem Abstand vom Zentralkörper ab.

Nach dem dritten Newton-Gesetz (Wechselwirkungsprinzip) muss der Trabant eine gleich große Kraft auf den Zentralkörper ausüben wie dieser auf ihn. Die Gravitationskraft muss daher auch proportional zur Masse M des Zentralkörpers sein:

Für die allgemeine Anziehung zweier Massen lautet also das Gravitationsgesetz

Die Proportionalitätskonstante heißt Gravitationskonstante. Sie wurde erstmals 1798 vom englischen Chemiker und Physiker Henry Cavendish gemessen. Ihr Wert ist

Bestimmung der Erdmasse

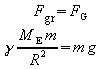Aufgelöst nach der Erdmasse M_E:

Bahnradius bzw. Umlaufdauer eines Satelliten

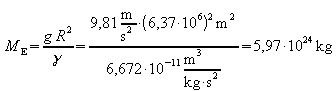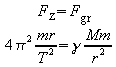a) Wenn die Umlaufdauer bekannt ist, kann der nötige Bahnradius ermittelt werden. Beispiel: Ein sogenannter geostationärer Satellit befindet sich stets über demselben Punkt der Erdoberfläche. Er dreht sich also genauso schnell wie die Erde, d.h. es ist T = 24 h. Dazu muss er den Bahnradius

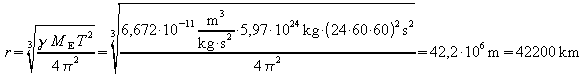
besitzen, sich also in der Höheüber der Erdoberfläche befinden.

b) Bei bekanntem Bahnradius lässt sich die Umlaufdauer vorausberechnen:

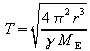Beispiel: Für eine Satellitenbahn in h = 500 km Höhe über der Erdoberfläche ist. Die Umlaufdauer beträgt dann

Bestimmung der Masse des Zentralkörpers

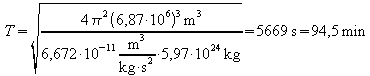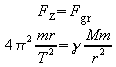
die Masse M des Zentralkörpers bestimmen:

Mit den Bahndaten der Erdeergibt sich die Sonnenmasse M_S:

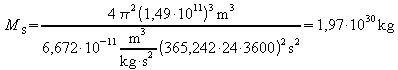Für den Jupitermond Io ist. Daraus ergibt sich die Jupitermasse

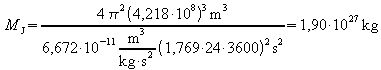Dies ist etwa das 318-fache der Erdmasse.

Numerische Berechnung von Satellitenbahnen

Die Bewegung des Satelliten wird in ihre x- und y-Komponente zerlegt.

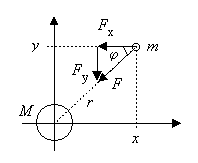
Für die Komponenten der Gravitationskraft ist abzulesen:

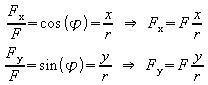Damit ergeben sich die Beschleunigungen:

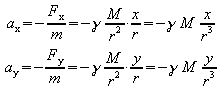Für die schrittweise Berechnung der Bahn werden Startwerte für den Zeitpunkt t = 0 benötigt:

Mit diesen werden zunächst die Beschleunigungen berechnet:

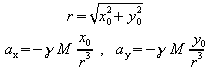Ausgehend von diesen Startwerten wird immer einen Zeitschritt weiter gerechnet:

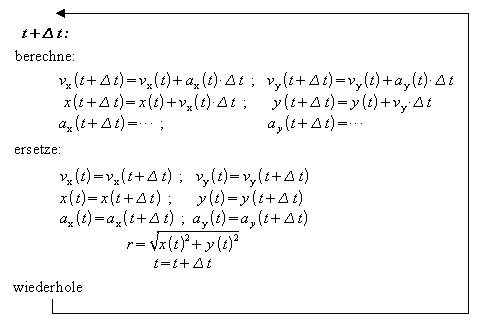
Die folgende Excel-Datei führt diese Berechnungen aus. Wenn Sie auf Ihrem Computer Excel installiert haben, können Sie diese Datei speichern und ausführen oder auch online ausführen. Klicken Sie dazu auf den folgenden Screenshot.

Beispiel: Bewegung eines Satelliten um die Erde

Hier ist . Für einen geostationären Satelliten (T = 24 h) wurde oben der Bahnradiusermittelt. Die Bahngeschwindigkeit beträgt

Startwerte für die Rechnung:

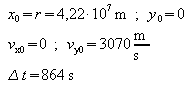
Damit ergibt sich die erwartete Kreisbahn.

Vorschläge für andere Startwerte:
 

Die folgende Abbildung zeigt eine elliptische Bahn des Satelliten um die Erde.

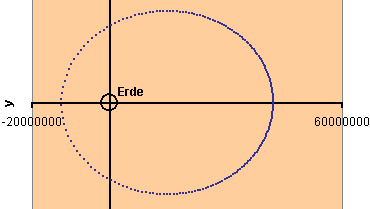
Wenn der Satellit sich in der Nähe der Erde befindet, ist der Abstand von je zwei aufeinanderfolgenden Punkten der berechneten Bahn größer als in größerer Entfernung von der Erde. Da zwischen zwei Punkten jeweils das gleiche Zeitintervallverstrichen ist bedeutet dies, dass die Bahngeschwindigkeit in Erdnähe größer ist als bei Erdferne. Am größten ist die Geschwindigkeit im erdnächsten Punkt (Perihel), am kleinsten im erdfernsten Punkt (Aphel).

Dies lässt sich verstehen, wenn man die Gravitationskraft in eine Komponente tangential zur Bahn und eine Komponente senkrecht zur Bahn zerlegt.

Die Gravitationskraft ist zu jedem Zeitpunkt der Bewegung auf den Zentralkörper gerichtet. Sie wird daher als Zentralkraft bezeichnet.

• Ihre Normalkomponente F_n bewirkt die Krümmung der Bahn nach innen: sie wirkt als Zentripetalkraft.
• Die Tangentialkomponente F_t dagegen beschleunigt den Satelliten. Entfernt sich der Satellit vom Zentralkörper, wirkt F_t entgegen der Bewegungsrichtung und verlangsamt den Satelliten. Nähert sich der Satellit dem Zentralkörper, dann wirkt F_t in Richtung der Bewegung und vergrößert damit die Bahngeschwindigkeit des Satelliten.

Umlaufdauer auf Ellipsenbahnen

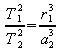Wenn der Radius der Kreisbahn so groß ist wie die große Halbachse der Ellipse ist, also r₁ = a₂, dann ist

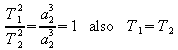Die Umlaufdauer T bei einer Kepler-Ellipse ist also genauso groß wie bei einer Kreisbahn mit einem Radius, der so groß ist wie die große Halbachse der Ellipse.

Sind M und a bekannt, dann ergibt sich daher aus dem Ansatz für Kreisbahnen

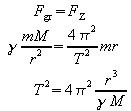
die Umlaufdauer auf der Ellipse, wenn r = a gesetzt wird:

Übungen

S.110, A2, A4

S.115, A2, A3 (Hinweis: Wenden Sie das zweite Kepler-Gesetz an.), A4, A5, A6, A7