Mechanische Schwingungen

Bewegungsfunktionen des Federpendels

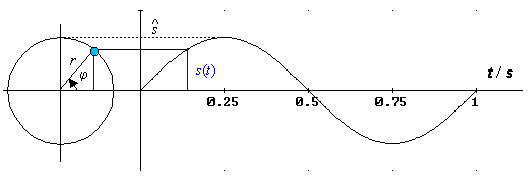
Die y-Komponente der Kreisbewegung stimmt mit der Bewegung des Federpendels überein. Es ist daher abzulesen:

Bei der gleichförmigen Kreisbewegung ist , also gilt für die Elongation des Federpendels

Die Projektion der Geschwindigkeits- und Beschleunigungsvektoren auf die y-Achse ergibt die Zeit-Geschwindigkeits- und die Zeit-Beschleunigungs-Funktion:
 

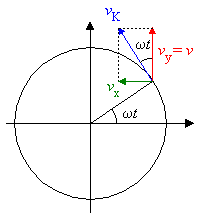
Mit der Bahngeschwindigkeit ergibt sich für die Geschwindigkeit des Federpendels:

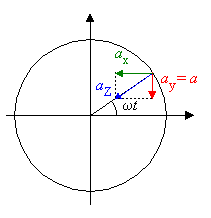
Mit der Zentripetalbeschleunigung ergibt sich für die Beschleunigung des Federpendels:

Eine andere Methode zur Bestimmung dieser Funktionen:

Ableiten der Zeit-Elongation-Funktion nach der Zeit ergibt die Zeit-Geschwindigkeit-Funktion des Pendelkörpers:

Nochmalige Ableitung führt auf die Zeit-Beschleunigung-Funktion:

Hier finden Sie zwei Java-Applets zum Federpendel:

http://www.schulphysik.de/java/physlet/applets/pendel2.html
(Braucht etwas Ladezeit... bitte nicht ungeduldig werden ;-)  )

http://www.walter-fendt.de/ph11d/federpendel.htm
( Dieses Applet sollte mit dem Internet Explorer betrachtet werden; mit anderen Browsern kann es Schwierigkeiten geben.)

Harmonische Schwingungen

Eine Schwingung, deren Zeit-Elongation-Funktion eine Sinusfunktion (oder Kosinusfunktion) ist, wird als harmonische Schwingung bezeichnet. Ein schwingungsfähiges System, das eine harmonische Schwingung ausführt, wird harmonischer Oszillator genannt.

1) Das Federpendel ist ein harmonischer Oszillator. Mit der Beschleunigung-Zeit-Funktion a(t) ergibt sich die Rückstellkraft der Feder:

Die Größe  heißt Richtgröße. Sie stimmt beim Federpendel mit der Federkonstanten überein. Das Minuszeichen zeigt an, dass die Rückstellkraft der Auslenkung stets entgegengerichtet ist. Die Größe wird als Kreisfrequenz bezeichnet.
 

Aus dem Vorliegen einer harmonischen Schwingung lässt sich also folgern, dass für die Rückstellkraft das lineare Kraftgesetz gilt.

Ist die Richtgröße bekannt, so kann die Periodendauer des Pendels bestimmt werden:

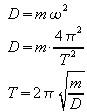
2) Nun sei umgekehrt ein System mit linearem Kraftgesetz  gegeben. Dann folgt aus

zunächst die Beschleunigung

Da die Beschleunigung die zweite Ableitung der Elongation ist, ergibt sich eine sog. Differentialgleichung:

Mit der Abkürzung

erhält man schließlich die Differentialgleichung des harmonischen Oszillators:

Diese Gleichung besitzt als Lösung z.B. die Sinusfunktion, denn:

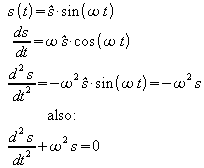
Aus dem Vorliegen des linearen Kraftgesetzes lässt sich also folgern, dass das betrachtete System eine harmonische Schwingung ausführt – also ein harmonischer Oszillator ist.

Beispiele für harmonische Schwingungen

1. Flüssigkeitsschwingungen

In einem U-Rohr mit Querschnitt A befindet sich eine Flüssigkeit, die z.B. durch Hineinblasen in Schwingung versetzt werden kann.

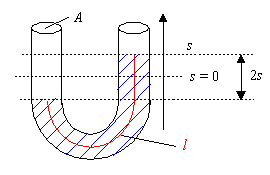
Als Rückstellkraft wirkt hier die Gewichtskraft der überstehenden Flüssigkeitssäule:

Das Volumen V dieser Flüssigkeitssäule ergibt sich aus „Grundfläche mal Höhe“, also

Die Rückstellkraft wird damit

Es liegt also ein lineares Kraftgesetz mit der Richtgröße

vor, d.h. die Schwingung ist eine harmonische Schwingung. Im Vergleich zur Schwingung eines Federpendels ist diese Schwingung wegen der Reibung der Flüssigkeit an den Rohrwänden stark gedämpft und klingt daher schnell ab (gedämpfte Schwingung – Gegensatz: ungedämpfte Schwingung).

Die Periodendauer der Schwingung ist

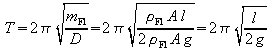Sie hängt nur von der Länge der Flüssigkeitssäule ab, nicht aber von der Dichte der Flüssigkeit.

2. Schwimmender Holzwürfel

Ein im Wasser schwimmender Holzwürfel (Seitenfläche A) verdrängt ein bestimmtes Wasservolumen V. Die Gewichtskraft des verdrängten Wassers wirkt als Auftriebskraft

Wird der Holzwürfel um eine Strecke s tiefer ins Wasser gedrückt, so nimmt das verdrängte Wasservolumen um

zu und damit vergrößert sich die Auftriebskraft:

Lässt man den Würfel los, so beginnt er um die anfängliche Gleichgewichtslage zu schwingen. Als Rückstellkraft wirkt die Veränderung der Auftriebskraft:

Es liegt also ein lineares Kraftgesetz mit der Richtgröße

vor. Auch diese Schwingung ist eine harmonische Schwingung.

3. Bewegung auf zwei schiefen Ebenen

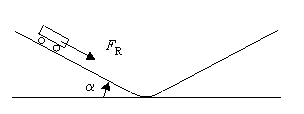
Als Rückstellkraft wirkt die Hangabtriebskraft:

Diese Kraft ist konstant. Da kein lineares Kraftgesetz vorliegt, ist die Bewegung keine harmonische Schwingung.

Energiebetrachtung

Die dem Federpendel beim Heben oder Senken des Pendelkörpers zugeführte Energie wird als Elongationsenergie bezeichnet. Lässt man den Pendelkörper los, so wandelt sich die Elongationsenergie periodisch in kinetische Energie des Pendelkörpers und umgekehrt um. Für die Summe dieser beiden Energien gilt zu jedem Zeitpunkt:

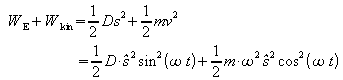
Unter Berücksichtigung von  wird daraus:

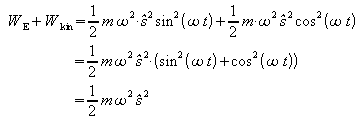
Die Gesamtenergie der Schwingung ist konstant:

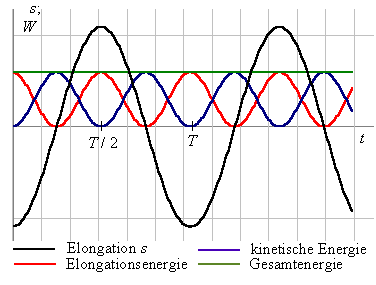
Die folgende Abbildung zeigt den zeitlichen Verlauf von Elongation, Elongationsenergie, kinetischer Energie und Gesamtenergie. Zu bemerken ist, dass die Zeitverläufe der Energien periodisch mit der halben Periodendauer T / 2 sind. (Wieso?)

Fadenpendel

Als Fadenpendel (oder mathematisches Pendel) wird ein an einem Faden aufgehängter Pendelkörper bezeichnet, wenn folgende Voraussetzungen erfüllt sind:

• die Masse des Fadens ist vernachlässigbar gegen die Masse m des Pendelkörpers;
• die Abmessungen des Körpers sind vernachlässigbar gegen die Länge l des Fadens.

Der Pendelkörper beschreibt einen Kreisbogen mit Radius l. Die Rückstellkraft ist hier die Komponente der Gewichtskraft des Pendelkörpers, die tangential zum Kreisbogen wirkt.

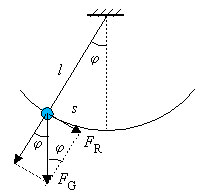
Für den Betrag der Rückstellkraft erhält man aus dem Kräfteparallelogramm:

Es liegt also kein lineares Kraftgesetz vor – die Schwingung des Fadenpendels ist nicht harmonisch.

Für kleine Winkel kann man den Sinus des Winkels näherungsweise durch den Winkel (im Bogenmaß) ersetzen:

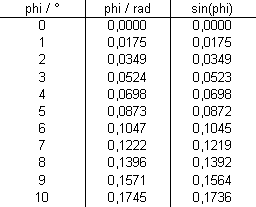
Für die Rückstellkraft gilt dann:

Bei kleiner Amplitude ist das Fadenpendel also näherungsweise ein harmonischer Schwinger mit der Richtgröße

und Periodendauer

Ein Fadenpendel der Länge l = 1 m hat demnach (für kleine Winkel) die Periodendauer T = 2,00 s.

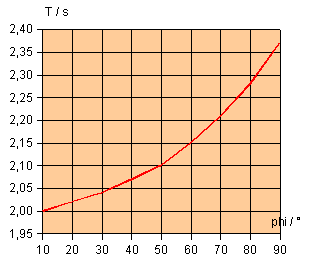
Die Abhängigkeit der Periodendauer von der Winkelamplitude lässt sich mit einer Simulation der Schwingung untersuchen. Mit einer Tabellenkalkulation wurden folgende Werte gefunden:
 

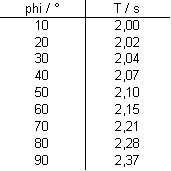Wenn Sie auf Ihrem Computer Excel installiert haben, können Sie die dazu verwendete Excel-Datei speichern und ausführen oder auch online ausführen. Klicken Sie dazu auf den folgenden Link: Fadenpendel.xls .

Ergänzung: Formale Behandlung des Fadenpendels

Beim Federpendel wurde die Pendelbewegung durch Angabe der Zeit-Elongation-Funktion s(t) beschrieben. Für das Fadenpendel können verschiedene Größen zur Beschreibung der periodischen Bewegung benutzt werden, z.B.:

• die Bogenlänge s(t) des Kreisbogens,
• der Auslenkungswinkel ,
• die Bewegung in vertikaler Richtung y(t).

Zwischen den Bahngrößen und den Winkelgrößen bestehen folgende Zusammenhänge:

Die x- und y-Koordinaten ergeben sich ebenfalls aus dem Auslenkungswinkel:

.

Es genügt also, die Schwingung des Fadenpendels durch Angabe des Auslenkungswinkels in Abhängigkeit von der Zeit zu beschreiben.

Zur Herleitung dieses Zusammenhanges wird wie oben die Rückstellkraft betrachtet:

.

Es ist wieder zu erkennen, dass kein lineares Kraftgesetz vorliegt: Die Rückstellkraft ist nicht proportional zur Auslenkung, die hier durch den Winkel beschrieben wird.

Die Rückstellkraft ist mit der Winkelbeschleunigung verknüpft:

Daraus folgt für :

.

Da sich die Winkelbeschleunigung aus der zweiten Ableitung des Auslenkungswinkels nach der Zeit ergibt, wird folgende Differentialgleichung erhalten:

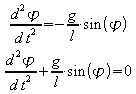
Für kleine Winkel kann wie oben auch die Näherung verwendet werden. Die Differentialgleichung für den Auslenkungswinkel nimmt dann die Form der Differentialgleichung des harmonischen Oszillators an:

Ein Vergleich mit

zeigt, dass für die Kreisfrequenz gilt:

.

Daraus ergibt sich die Periodendauer

.

(Bemerkung: Beim Federpendel wurde die Kreisfrequenz mit bezeichnet, da sie mit der Winkelgeschwindigkeit eines synchron zum Pendelkörper auf einer Kreisbahn mit Radius umlaufenden Körpers übereinstimmte: . Beim Fadenpendel bedeutet aber die zeitabhängige Winkelgeschwindigkeit der beschleunigten Bewegung des Pendelkörpers auf dem Kreisbogen: . Die Kreisfrequenz wird deswegen zur Unterscheidung davon mit bezeichnet.)

Die Lösungen der Differentialgleichung für kleine Winkel sind – wie beim Federpendel – Sinus- und Cosinusfunktionen, z.B.:

.

Für die Winkelgeschwindigkeit und die Winkelbeschleunigung folgt daraus:

,

.

Wenn das Fadenpendel um einen bestimmten Winkel ausgelenkt und zur Zeit t = 0 frei gegeben wird, dann wird die Bewegung durch eine Cosinusfunktion beschrieben:

.

Daraus folgt weiter:

,

Übungen

(Die zuerst angegebenen Seitenzahlen beziehen sich auf den Teilband 11. Die Seitenzahlen für den Gesamtband stehen in Klammern.)
 

empfohlene Aufgaben aus dem Lehrbuch	Lösungen
S.134 (274), A1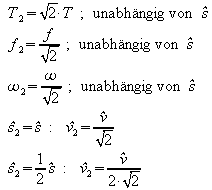
S.134 (274), A2	a) vmax = 0,628 m/s b) D = 2,96 N/m c) nein
S.276, A1	T = 16,4 s
S.276, A2	l = 0,248 m
S.276, A3	g = 9,816 m/s2
S.136 (279), A1
S.136, A4, a, b (S.279, A2, a, b)	a) f = 1,58 s-1 b) W = 0,049 J
S. 279, A3	vmax = 0,503 m/s s = 8,67 cm

Weitere Übungen

1. Eine Schraubenfeder hat die Richtgröße D = 10 N/m. Welche Masse m muss ein an die Feder gehängter Körper haben, damit die Periodendauer des Federpendels  beträgt?

2. Ein Körper der Masse m = 300 g hängt an einer Schraubenfeder. Er führt harmonische Schwingungen aus: . Die Periodendauer beträgt , die Amplitude beträgt .
a) Berechnen Sie die Richtgröße der Schraubenfeder.
b) Wie groß ist die Geschwindigkeit des Körpers beim Durchgang durch die Gleichgewichtslage?
c) Berechnen Sie die Beschleunigung a beim Durchgang durch die Gleichgewichtslage und zur Zeit der größten Elongation.

3. An einer Schraubenfeder hängt ein Körper der Masse m = 200 g. Durch die vertikal nach unten wirkende Kraft F = 0,5 N wird der Körper zunächst um die Strecke s_max = 10 cm aus seiner Gleichgewichtslage ausgelenkt. Der Körper wird dann losgelassen und führt eine freie Schwingung aus.
a) Berechnen Sie die Periodendauer der Schwingung.
b) Berechnen Sie die maximale Geschwindigkeit.
c) Berechnen Sie die maximale Elongationsenergie der Feder und die maximale kinetische Energie des Körpers.

4. Ein Sekundenpendel ist ein Fadenpendel, das für eine halbe Schwingung die Zeit 1 s benötigt. Wie groß ist die Pendellänge eines Sekundenpendels
a) an den Polen (g₁ = 9,83 m/s²), b) in Mitteleuropa (g₂ = 9,81 m/s²),
c) am Äquator (g₃ = 9,78 m/s²)?

5. Um die Sehne einer Armbrust um 1 cm aus ihrer Gleichgewichtslage zu ziehen, benötigt man eine Kraft von 20 N. Angenommen, es gelte das lineare Kraftgesetz. Mit welcher Geschwindigkeit könnte man einen Pfeil der Masse m = 20 g abschießen, wenn man die Sehne um 10 cm gespannt hat? Wie lange dauert der Beschleunigungsvorgang?

6. Ein Ball (m = 50 g) wird durch sein Eigengewicht um 0,1 mm eingedrückt. Nehmen Sie vereinfachend an, dass für die Verformung des Balls ein lineares Kraftgesetz gilt.
a) Wie weit wird der Ball zusammengedrückt, wenn er mit einer Geschwindigkeit von 20 m/s elastisch gegen eine Wand prallt?
b) Wie groß ist die Kontaktzeit mit der Wand?

7. An einer Schraubenfeder hängt eine Kugel (m = 100g). Sie wird um 4 cm aus der Gleichgewichtslage ausgelenkt und führt eine harmonische Schwingungmit der Periodendauer von 1 s aus.
a) Wie groß ist die Elongation zur Zeit t = 0,125 s? Zeichnen Sie das Zeit-Ort-Diagramm für die Zeit t = 0 ... 1,25 s. (Maßstab: t-Achse: 1 cm für 0,25 s; s-Achse: 1 cm für 2 cm Auslenkung)
b) Wie groß ist der maximale Geschwindigkeitsbetrag? Zu welchen Zeiten und bei welchen Elongationen wird diese Geschwindigkeit jeweils erreicht?
c) Berechnen Sie den maximalen Beschleunigungsbetrag und den Betrag der maximalen Beschleunigungskraft. Zu welchen Zeiten und bei welchen Elongationen werden diese Werte jeweils erreicht?
d) Berechnen Sie für die Zeit t = 0,65 s jeweils die Elongation s, die Geschwindigkeit v und die Beschleunigung a. Geben Sie auch die Richtung dieser Größen an.
e) Bei welcher Elongation wird die Kugel mit der Kraft F = 0,1 N nach unten beschleunigt?
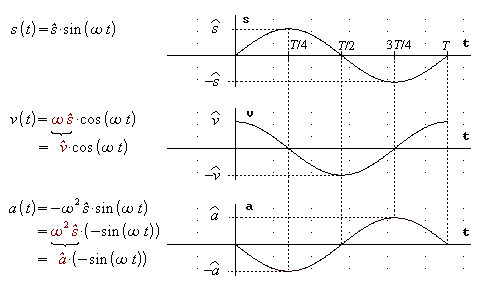
f) Skizzieren Sie das t-v- und das t-a-Diagramm der Schwingung.
g) Wie groß ist die Beschleunigung der Kugel 1 cm über der Gleichgewichtslage?
 
 

Lösungen

1. m = 0,625 kg

2. a) D = 4,8 N/m

b) v_max = 0,48 m/s

c) Gleichgewichtslage: a = 0;
größte Elongation: a = a_max = 1,92 m/s²

3. a) T = 1,26 s

b) v_max = 0,499 m/s

c) W_E = 0,025 J, W_kin = 0,025 J

4. a) l₁ = 0,996 m

b) l₂ = 0,994 m

c) l₃ = 0,991 m

5. v_max = 31,6 m/s

Beschleunigungsdauer: t_a = T/4 = 4,97 ms

6. a) s_max = 6,4 cm

b) Kontaktzeit: t_K = T/2 = 10 ms

7. a) (t-s-Diagramm wie oben)

b) v_max = 0,251 m/s ;

wird erreicht bei t = 0, s = 0 und t = T/2, s = 0 und t = T, s = 0.

c) a_max = 1,58 m/s² , F_max = 0,158 N ;

wird erreicht bei t = T/4, s = s_max und t = 3T/4, s = –s_max

d) s(0,65 s) = –3, 236 cm

v(0,65 s) = –14,75 cm/s , nach unten gerichtet

a(0,65 s) = 127, 7 cm/s² , nach oben gerichtet

e) s = 2,53 cm

f) (t-v-Diagramm und t-a-Diagramm wie oben)

g) a = –39,5 cm/s²