Wie groß müssen l und r gewählt werden, damit das Spielfeld (die Rechtecksfläche) möglichst groß wird? Wie groß ist dann der maximale Flächeninhalt?
Beispiel 1: Maße eines Sportplatzes
| Eine 400-m-Laufbahn besteht aus zwei
parallelen Strecken der Länge l und zwei angesetzten Halbkreisen
mit Radius r.
Wie groß müssen l und r gewählt werden, damit das Spielfeld (die Rechtecksfläche) möglichst groß wird? Wie groß ist dann der maximale Flächeninhalt? |
|
Der Flächeninhalt des Rechtecks beträgt
und hängt von beiden Variablen des Problems ab. Nun hängen aber r und l gemäß der Aufgabenstellung zusammen, denn die beiden geraden Strecken und die beiden Halbkreise müssen zusammen 400 (m) ergeben:
.
Aus dieser Bedingung ergibt sich
.
Wird diese Beziehung in den Term für den Flächeninhalt eingesetzt, so ergibt sich
.
Der Flächeninhalt des Rechtecks ist jetzt nur noch Funktion der einen Variablen r.
Die Definitionsmenge des Terms A(r)
ist 
.
Vom Problem her sind aber nur nicht-negative Radien sinnvoll: 
.
Der größte mögliche Wert für r ergibt sich,
wenn l = 0 ist: 
.
Definitionsmenge der Flächeninhaltsfunktion ist also
.
An den Randpunkten gilt:
links: r = 0: l = 200; A(0) = 0 Der Sportplatz entartet zu einer Doppelstrecke.
rechts: 
:
l
= 0; 
Der Sportplatz entartet zu einem Vollkreis.
Bestimmung der lokalen Extrema:
notwendige Bedingung: 
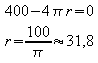
hinreichende Bedingung: 
Da
ist, ist 
lokale Maximalstelle.
Das lokale Maximum beträgt
.
Da an den Rändern der Definitionsmenge von
A
der Funktionswert jeweils 0 ist, ist 
nicht nur ein lokales Maximum, sondern der größte Funktionswert,
der in ganz DA angenommen wird (globales Maximum).
Für l ergibt sich
.
Ergebnis: Das rechteckige Spielfeld wird möglichst groß, wenn r = 31,8 m und l = 100 m gewählt werden. Es hat dann den maximalen Flächeninhalt 6366 m2.
Dies sind tatsächlich übliche Maße von Sportplätzen: An der Längsseite befindet sich die 100-m-Laufbahn, und die Aschenbahn (Umfang) hat die Gesamtlänge von 400 m.
Das Beispiel zeigt die einzelnen Schritte, die
beim Lösen von Extremwertproblemen mit Nebenbedingungen auszuführen
sind.
| Strategie zum Lösen
von Extremwertproblemen mit Nebenbedingungen:
1. Beschreiben der Größe, die extremal werden soll, durch einen Term. Diese Extremalbedingung kann mehrere Variable enthalten. 2. Aufsuchen von Nebenbedingungen, d.h. Herstellen von Beziehungen zwischen den Variablen anhand der Aufgabenstellung. 3. Einsetzen der Nebenbedingung(en) in die Extremalbedingung, so dass eine Funktion mit nur einer Variablen, die Zielfunktion, entsteht. 4. Untersuchung der Zielfunktion auf Extremwerte:
5. Formulierung des Ergebnisses und Plausibilitätsprüfung. |
Beispiel 2:
Dem Teil des Graphen der Funktion f mit 
,
der oberhalb der x-Achse verläuft, ist ein Rechteck so einzubeschreiben,
dass sein Flächeninhalt möglichst groß wird.
1. Extremalbedingung:
Der Graph ist eine nach unten geöffnete Parabel mit Scheitelpunkt [0; 4]. Die Nullstellen von f sind
.
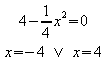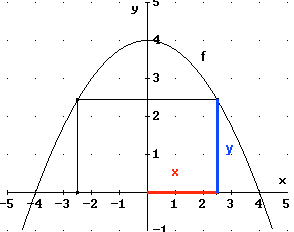
Die eine Seite des einbeschriebenen Rechtecks liegt auf der x-Achse, die andere Seite ist parallel zur y-Achse. Die Fläche dieses Rechtecks ergibt sich aus
.
2. Nebenbedingung:
Da die oberen Eckpunkte des Rechtecks auf der Parabel liegen, ist y = f (x).
3. Zielfunktion:
.
4. Untersuchung der Zielfunktion auf Extremwerte:
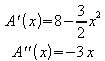
notwendige Bedingung: 
.
Die erste Lösung liegt nicht in DA.
hinreichende Bedingung: 
,
ist also lokale Maximalstelle von A.
Lokales Maximum: 
Randwerte:
Somit ist das lokale Maximum auch das globale Maximum.
Für y ergibt sich:
.
5. Ergebnis:
Der Flächeninhalt des Rechtecks wird möglichst
groß, wenn
und 
gewählt werden. Er beträgt dann 
.
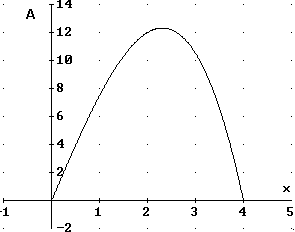
Der Graph der Flächenfunktion zeigt, dass für etwa x = 2,3 der Flächeninhalt maximal wird und dann ungefähr A = 12,2 beträgt.
Beispiel 3:
Gegeben ist die Funktion f mit 
.
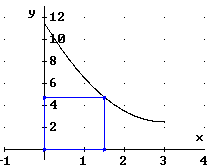
Von allen achsenparallelen Rechtecken mit dem
Ursprung als einem Exkpunkt und dem Punkt
P(x | f (x)) als gegenüberliegendem
Eckpunkt ist dasjenige mit maximalem Inhalt zu bestimmen.
1. Extremalbedingung:
Die Rechteckfläche ergibt sich aus
.
2. Nebenbedingung:
Da der rechte obere Eckpunkt des Rechtecks auf der Parabel liegt, ist y = f (x).
3. Zielfunktion:
Einsetzen der Nebenbedingung in die Extremalbedingung führt auf
.
4. Untersuchung der Zielfunktion auf Extremwerte:
Aus A' (x) = 0 ergeben sich die Lösungen
.
Die Auswertung der hinreichenden Bedingung führt auf
.
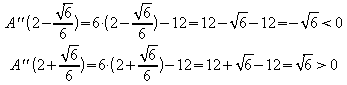ist also lokale Maximalstelle und 
ist lokale Minimalstelle.
Lokales Maximum:
.
Randwerte:
.
Der Randwert A(3) ist größer als das lokale Maximum von A, somit stellt der Randwert das globale Maximum dar.
5. Ergebnis:
Der Flächeninhalt des Rechtecks wird möglichst groß, wenn x = 3 und y = 2,5 gewählt werden. Er beträgt dann Amax .= 7,5.
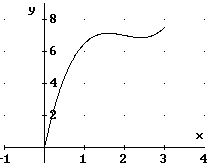
Der Graph der Flächeninhaltsfunktion lässt erkennen, dass das globale Maximum tatsächlich ein Randmaximum ist.
Beispiel 4:
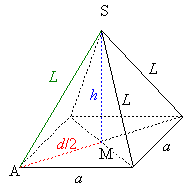
| Aus vier 3 m langen Stangen soll
ein Zelt mit quadratischer Grundfläche zusammengestellt werden. Wie
hoch wird es, wenn sein Rauminhalt maximal sein soll?
Folgende Bezeichnungen werden eingeführt: L: Länge der Stangen
|
 |
1. Extremalbedingung:
Das Volumen der Pyramide ist
.
2. Nebenbedingungen:
Dem Dreieck AMS ist zu entnehmen:
.
Für die Quadratdiagonale gilt
.
Wird dies in die Beziehung für L2 eingesetzt, so folgt
.
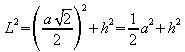3. Zielfunktion
| Umgestellt nach a2:
Einsetzen in die Extremalbedingung ergibt die Volumenfunktion
Die Höhe h kann nur Werte zwischen 0 und 3 m annehmen, also ist
|
Umgestellt nach h:
Einsetzen in die Extremalbedingung:
Die Seite des Grundquadrats kann Werte zwischen
0 und
|
Die Zielfunktion mit der Variablen h ist leichter weiter zu behandeln, da sie eine ganzrationale Funktion darstellt.
4. Untersuchung der Zielfunktion auf Extremwerte:
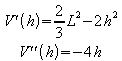
Die Auswertung von V' (h) = 0 ergibt
.
Da h > 0 sein muss, scheidet die negative Lösung aus. Für den positiven Wert erhält man
,
so dass es sich um eine lokale Maximalstelle handelt.
Lokales Maximum:
.
Randwerte: V(0) = V(3) = 0. Das lokale Maximum ist also auch globales Maximum.
Für a ergibt sich
.
5. Ergebnis:
Wenn der Rauminhalt maximal ist, beträgt
die Höhe des Zeltes 
.
Die Länge der Seite des Grundquadrates ist dann 
und das Volumen beträgt 
.
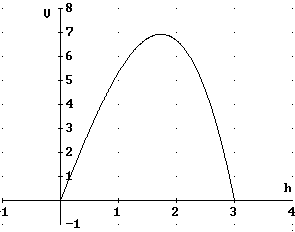
Dem Graphen der Volumenfunktion ist zu entnehmen, dass für etwa h = 1,75 m das Volumen maximal wird und etwa den Wert 7 m3 annimmt..
Übungen
1. Ein Rechteck habe den Umfang 12 cm. Wie lang sind die Rechteckseiten zu wählen, damit das Rechteck maximalen Flächeninhalt hat?
2. Aus einem rechteckigen Stück Blech gegebener Länge soll eine gleich lange Röhre mit möglichst großem, rechteckigen Querschnitt hergestellt werden.
3. Welche zylindrische Dose mit dem Oberflächeninhalt von 1 dm2 hat das größte Volumen?
4. Ein Dachboden hat als Querschnittsfläche
ein gleichschenkliges Dreieck mit einer Höhe von 4,8 m und einer Breite
von 8 m. In ihm soll ein möglichst großes quaderförmiges
Zimmer eingerichtet werden.
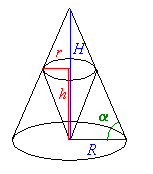
| 5. Einem Kegel soll ein zweiter Kegel
mit möglichst großem Volumen so einbeschrieben werden, dass
die Spitze des zweiten Kegels im Mittelpunkt des Grundkreises des ersten
Kegels liegt.
Anleitung: Zeigen Sie zunächst, dass gilt
|
 |
6. Ein Betrieb hat die Kostenfunktion K
mit 
,
wobei x die Anzahl der hergestellten Mengeneinheiten bezeichnet.
Der Verkaufspreis betrage pro Mengeneinheit p = 200. Nehmen Sie
an, dass sich zu diesem Stückpreis stets alle produzierten Mengeneinheiten
verkaufen lassen. Für welche Produktionsmenge wird der Gewinn maximal?
.
.
.
.
annehmen, also ist hier
.