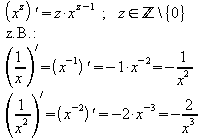5. Lokale Extrema

Vorübungen

1. Zeichnen Sie den Graphen von

sowie die Graphen von  und .

a) Wo ist f ' (x) = 0?
     Welche Eigenschaften hat der Graph von f an diesen Stellen?

b) Wo ist f '' (x) = 0?
     Welche Eigenschaften hat der Graph von f ' an diesen Stellen?
     Wie verhält sich der Graph von f an diesen Stellen?

2. Zeichnen Sie den Graphen von

sowie die Graphen von  und .

a) Wo ist f ' (x) = 0?
     Welche Eigenschaften hat der Graph von f an diesen Stellen?

b) Wo ist f '' (x) = 0?
     Welche Eigenschaften hat der Graph von f ' an diesen Stellen?
     Wie verhält sich der Graph von f an diesen Stellen?

5.1 Begriffe

In den Vorübungen traten immer wieder Stellen x auf, für die man sagen konnte: In einer Umgebung von x nimmt die jeweils betrachtete Funktion f den größten oder kleinsten Wert an. Folgende Begriffe werden bei der Beschreibung solcher Sachverhalte benutzt.
 
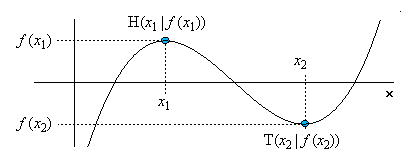
x1: lokale Maximalstelle
f (x1): lokales Maximum
H(x1| f (x1)): Hochpunkt des Graphen von f		 x2: lokale Minimalstelle
f (x2) lokales Minimum
T(x2| f (x2)): Tiefpunkt des Graphen von f

Als zusammenfassende Begriffe werden verwendet:

Definition: Eine Funktion f sei in einem Intervall A definiert. Dann liegt bei  ein 
lokales Maximum
lokales Minimum
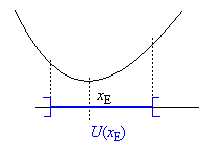
genau dann, wenn es eine Umgebung  gibt mit der Eigenschaft 
für alle .

5.2 Notwendige Bedingung für lokale Extrema

Bei „glatt“ verlaufendem Graphen von f lässt die Anschauung erwarten, dass in einem lokalen Extrempunkt des Graphen von f die Tangente waagerecht verläuft. Tatsächlich gilt der folgende
 
Satz (notwendige Bedingung für lokale Extrema):

Sei die Funktion f an der Stelle xE differenzierbar. Wenn f an dieser Stelle ein lokales Extremum hat, dann ist f ' (xE) = 0 an dieser Stelle.

Beachte: Die Umkehrung des Satzes: „Wenn f ' (xE) = 0 ist, dann hat f an der Stelle xE ein lokales Extremum.“ gilt nicht. Ein Beispiel macht dies sofort einsichtig:

f (x) = x3 ; f ' (x) = 3x2

Nun ist zwar f ' (0) = 0, aber x = 0 ist keine lokale Extremstelle, denn:
Für x < 0 ist f (x) < f (0), und für x > 0 ist f (x) > f (0).
Es gibt also keine Umgebung U(0), so dass  ist.

Anders ausgedrückt: Die Lösungen der Gleichung f ' (x) = 0 sind mögliche lokale Extremstellen von f. Ob sie es wirklich sind, und wenn ja, von welcher Art sie sind (Maximal- oder Minimalstellen), muss noch untersucht werden.

Übungen:

Bestimmen Sie die möglichen lokalen Extremstellen von f .

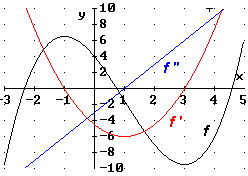
5.3 Hinreichende Bedingung für lokale Extrema

Untersucht man bei „glatten“ Graphen das Verhalten der Steigung in einer Umgebung einer lokalen Extremstelle, so findet man folgende Zusammenhänge.


 

1. a) Links von einer lokalen Maximalstelle (im Beispiel: xmax = –1) besitzt der Graph von f Tangenten mit positiver Steigung. Geht man auf der x-Achse nun weiter nach rechts (in Richtung Maximalstelle), so nimmt die Tangentensteigung ab, bis sie schließlich an der Maximalstelle den Wert 0 erreicht. An Stellen x > xmax besitzt der Graph von f Tangenten mit negativer Steigung. Die Tangentensteigung nimmt also – von links nach rechts – laufend ab.

b) Die Steigung der Tangenten an den Graphen von f ist durch die Ableitung f ' gegeben. Daher muss der Graph von f ' in der betrachteten Umgebung der Maximalstelle xmax fallen. Das bedeutet, er besitzt hier Tangenten mit negativer Steigung.

c) Die Steigung der Tangenten an den Graphen der Ableitung f ' ist durch die zweite Ableitung f '' gegeben. Daher muss f '' in der betrachteten Umgebung der lokalen Maximalstelle von f negativ sein. Insbesondere gilt dann f '' (xmax) < 0.

2. a) Links von einer lokalen Minimalstelle (im Beispiel: xmin = 3) besitzt der Graph von f Tangenten mit negativer Steigung. Geht man auf der x-Achse nun weiter nach rechts (in Richtung Minimalstelle), so nimmt die Tangentensteigung zu, bis sie schließlich an der Minimalstelle den Wert 0 erreicht. An Stellen x > xmin besitzt der Graph von f Tangenten mit positiver Steigung. Die Tangentensteigung nimmt also – von links nach rechts – laufend zu.

b) Die Steigung der Tangenten an den Graphen von f ist durch die Ableitung f ' gegeben. Daher muss der Graph von f ' in der betrachteten Umgebung der Minimalstelle xmin steigen. Das bedeutet, er besitzt hier Tangenten mit positiver Steigung.

c) Die Steigung der Tangenten an den Graphen der Ableitung f ' ist durch die zweite Ableitung f '' gegeben. Daher muss f '' in der betrachteten Umgebung der lokalen Minimalstelle von f positiv sein. Insbesondere gilt dann f '' (xmin) > 0.

Der Anschauung werden folgende Sätze entnommen.
Satz 1 ( hinreichende Bedingung für lokale Extrema / Vorzeichenwechselkriterium):

Sei f an der Stelle xE und in einer Umgebung von xE differenzierbar.
Wenn f ' (xE) = 0 ist und f ' an der Stelle xE einen Vorzeichenwechsel von + nach – hat, 
dann ist f ' (xE) lokales Maximum.
Wenn f ' (xE) = 0 ist und f ' an der Stelle xE einen Vorzeichenwechsel von – nach + hat, 
dann ist f ' (xE) lokales Minimum.
Satz 2 (hinreichende Bedingung für lokale Extrema / zweite Ableitung):

Ist eine Funktion f an einer Stelle xE zweimal differenzierbar und gilt 
,
,
so hat die Funktion an der Stelle xE ein
lokales Maximum.
lokales Minimum.

Beispiel (1):

Die Auswertung der notwendigen Bedingung für lokale Extrema liefert mögliche Extremstellen:

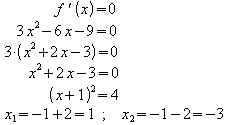
Die Auswertung der hinreichenden Bedingung liefert die Aussage, ob es sich wirklich um lokale Extremstellen handelt und welcher Art die Extremstellen sind:

,

das bedeutet: x1 ist eine lokale Minimalstelle;

,

das bedeutet: x2 ist lokale Maximalstelle.

Beispiel (2):

Dieses Beispiel soll verdeutlichen, dass die hinreichende Bedingung in der Form des obigen Satzes 2 nicht immer erfüllt ist.

Auswertung der notwendigen Bedingung für lokale Extrema:

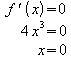
Auswertung der hinreichenden Bedingung:

,

das bedeutet: es ist keine Entscheidung möglich, ob es sich um eine lokale Extremstelle handelt.

Die Bedingung ist eben nur hinreichend, aber nicht notwendig. Das heißt, wenn f an der Stelle xE ein lokales Maximum (Minimum) hat, dann gilt nicht notwendig  (bzw. ).

Es steht aber noch das Vorzeichenwechsel-Kriterium als hinreichende Bedingung zur Verfügung. Die Ableitung f ' hat x = 0 als einzige Nullstelle. Wählt man z.B. x1 = -1 und x2 = +1, so ergibt sich

das bedeutet: f ' hat an der Stelle x = 0 einen Vorzeichenwechsel von – nach +,

also ist x = 0 lokale Minimalstelle von f.

Beispiel (3):

Es gibt aber auch Fälle, in denen das Vorzeichenwechsel-Kriterium nicht weiter hilft.

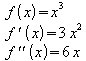
Auswertung der notwendigen Bedingung für lokale Extrema:

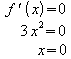
Auswertung der hinreichenden Bedingung (schwächeres Kriterium mit der zweiten Ableitung):

,

das bedeutet: es ist keine Entscheidung möglich, ob es sich um eine lokale Extremstelle handelt.

Auswertung der hinreichenden Bedingung (Vorzeichenwechsel-Kriterium):

Es ist sowohl für x < 0 wie für x > 0 stets f ' (x) > 0 ,

das bedeutet: es ist keine Entscheidung möglich, ob es sich um eine lokale Extremstelle handelt.

(Tatsächlich liegt ein sogenannter „horizontaler Wendepunkt“ (auch „Sattelpunkt“ genannt) vor. Mit Wendepunkten beschäftigt sich der nächste Abschnitt.)

Übungen:

Zur Darstellung der Graphen der Funktionen und ihrer Ableitungen kann das Applet „Untersuchung ganz-rationaler Funktionen“ verwendet werden.

     

Bestimmen Sie bei den folgenden Funktionen jeweils lokale Extremstellen, lokale Extrema und Extrempunkte des Graphen.

1.

2.

3.

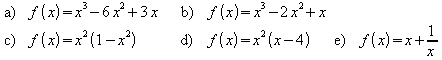
Hinweis zu e): Die Potenzregel, die bisher nur für Exponenten n > 0 bewiesen wurde, gilt auch für ganzzahlige Exponenten, die von Null verschieden sind: