[Pythagoras von Samos, etwa 580 bis etwa 500 v.Chr.]
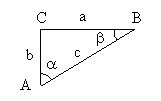
Betrachtet wird ein rechtwinkliges Dreieck mit rechtem Winkel bei C.
Die Dreiecksseite, die dem rechten Winkel gegenüber liegt, wird Hypotenuse genannt. Die Seiten, die die Schenkel des rechten Winkels bilden, heißen Katheten. Da g ein rechter Winkel ist, gilt
.Es werden vier solcher Dreiecke so zusammen gelegt, dass ein Quadrat mit denSeiten a + b entsteht. (Mit einem Klick auf die Schaltfläche "nächstes Bild" wird der Aufbau der Figur schrittweise demonstriert.)
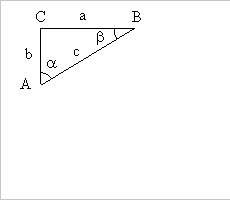
Darin liegt ein Viereck mit Seitenlänge c. Die Winkel d i sind rechte Winkel, denn es gilt jeweils:
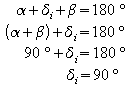
Das entstandene innere Viereck ist also ein Quadrat.
Der Flächeninhalt A1 des größeren Quadrates lässt sich zusammensetzen aus dem Flächeninhalt A2 des kleineren Quadrats und dem Flächeninhalt AD der 4 Dreiecke:
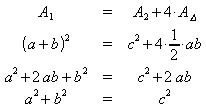
Das ist der berühmte
Satz des Pythagoras: In einem rechtwinkligen Dreieck
mit den Katheten a und b und der Hypotenuse c gilt
 .In einem rechtwinkligen Dreieck ist die Summe der Flächeninhalte der Quadrate über den Katheten gleich dem Flächeninhalt des Quadrats über der Hypotenuse. |
Es gilt auch die
Umkehrung des Satz des Pythagoras:
Wenn für die Seiten a, b, c eines Dreiecks gilt ,
dann ist das Dreieck rechtwinklig mit c als Hypotenuse und a
und b als Katheten. |
[Euklid von Alexandrien, etwa 365 bis etwa 300 v.Chr.]
Im rechtwinkligen Dreieck ABC wird die Höhe h auf die Seite
c errichtet. Sie trifft die Hypotenuse im Punkt D und teilt die
Hypotenuse in zwei Teilstrecken
.
p und q werden Hypotenusenabschnitte genannt.
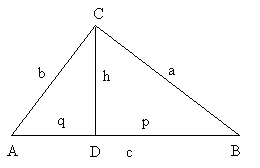
Im Teildreieck CAD gilt nach dem Satz des Pythagoras
,
und im Teildreieck BCD gilt
.Addition führt dann auf
und weiter:
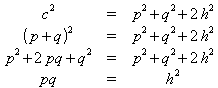.Dies ist der
Höhensatz des Euklid: In
einem rechtwinkligen Dreieck mit der Höhe h und den Hypotenusenabschnitten
p
und q gilt
 . |
Im Teildreieck CAD gilt nach dem Satz des Pythagoras
.
Mit dem Höhensatz ergibt sich daraus
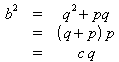
Im Teildreieck BCD folgt aus dem Satz des Pythagoras und dem Höhensatz
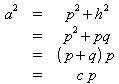
Die Beziehungen für a2 und b2
fasst man zusammen zum
Kathetensatz des Euklid: In einem
rechtwinkligen Dreieck mit der Hypotenuse c, den Katheten
a
und b und den Hypotenusenabschnitten p und q gilt
 .Geometrische Deutung: In einem rechtwinkligen Dreieck ist der Flächeninhalt des Quadrats über einer Kathete gleich dem Flächeninhalt des Rechtecks aus der Hypotenuse und dem der Kathete anliegenden Hypotenusenabschnitt. |
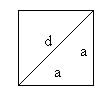
In einem Quadrat der Seitenlänge a gilt nach dem Satz des Pythagoras für die Länge der Diagonale
,
also:
.
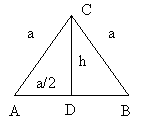
Nach dem Satz des Pythagoras gilt im Teildreieck CAD:
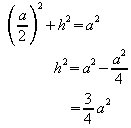
also:
.Für den Flächeninhalt A des gleichseitigen Dreiecks ergibt sich:
.
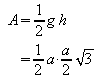
Eine Pyramide mit quadratischer Grundfläche (quadratische Pyramide) habe die Grundseite a, die Seitenkante s und die Höhe h.
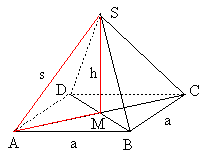
Für die Höhe h gilt nach dem Satz des Pythagoras im Dreieck AMS:
Für die Länge der Diagonale
gilt
.Damit ist
,und für die Pyramidenhöhe folgt:
,
.
Im Koordinatensystem seien zwei Punkte P1 = (x1 ; y1) und P2 = (x2 ; y2) gegeben.
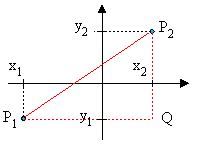
Der Abstand d von P1 und P2 ist die Länge
der Strecke
.
Im rechtwinkligen Dreieck P1QP2 ist die Länge
der Kathete
gleich
x2
– x1, und die Länge der Kathete
ist
gleich y2 – y1. Nach dem Satz des Pythagoras
folgt
.
Die Grundfläche eines Quaders sei ein Rechteck mit den Seiten a und b, die Höhe des Quaders sei c.
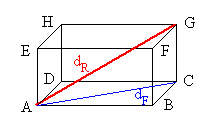
Für die Flächendiagonale dF der Grundfläche gilt nach dem Satz des Pythagoras im Dreieck ABC :
.Die Raumdiagonale dR ist die Hypotenuse im rechtwinkligen Dreieck ACG; aus dem Satz des Pythagoras folgt
,also:
.Für den Spezialfall des Würfels (a = b = c) erhält man
.
Übungen
1. Berechnen Sie die fehlenden Größen für ein rechtwinkliges Dreieck ABC mit der Hypotenuse AB.
| a) | b) | c) | d) | e) | f) | g) | |
|---|---|---|---|---|---|---|---|
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
|
||||||
|
|
|
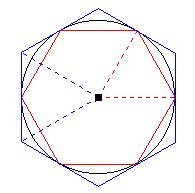
2. Einem Kreis mit dem Radius r = 5 cm wird jeweils ein regelmäßiges
Sechseck einbeschrieben und umbeschrieben. Berechnen Sie den Flächeninhalt
der beiden Sechsecke.
(Sie erhalten damit eine Abschätzung für den Flächeninhalt
des Kreises mit dem Radius r.)
3. a) Grundseite und Höhe eines gleichschenkligen Dreiecks sind jeweils 7 cm lang. Berechnen Sie die Schenkellänge.
b) In einem gleichschenkligen Dreieck ist die Grundseite 6 cm und ein Schenkel 8 cm lang. Berechnen Sie die Höhe und den Flächeninhalt des Dreiecks.
c) Ein gleichschenkliges Dreieck hat die Grundseite a = 5 cm und den Flächeninhalt A = 15 cm². Berechnen Sie Höhe und Schenkellänge.
d) Wie lang ist die Höhe in einem gleichschenkligen Dreieck, bei
dem ein Schenkel doppelt so lang ist wie die Grundseite?
4. a) Bei einer quadratischen Pyramide ist s die Länge der Seitenkante, h die Höhe und und a die Länge der Grundseite. Berechnen Sie jeweils das fehlende Stück.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) Geben Sie die Formel an, mit der man die Länge der Seitenkante einer quadratischen Pyramide berechnen kann, wenn man die Pyramidenhöhe h und die Länge a der Grundseite kennt.
c) Mit welcher Formel kann man die Länge a der Grundseite
einer quadratischen Pyramide berechnen, wenn man die Pyramidenhöhe
h
und die Länge s der Seitenkanten kennt?
5. a) Ein regelmäßiges Tetraeder ist eine aus vier gleichseitigen
Dreiecken bestehende Pyramide. Die Tetraederhöhe verläuft von
der Spitze D zum Schwerpunkt S der Grundfläche (Eckpunkte A, B, C);
sie steht senkrecht auf der Grundfläche.
Wie lang ist die Tetraederhöhe, wenn die Grundseite des Tetraeders
die Länge a hat?
(Hinweis: Der Schwerpunkt S teilt die Seitenhalbierenden, d.h. beim
gleichseitigen Dreieck auch die Höhen, im Verhältnis 1:2.)
b) Ein regelmäßiges Tetraeder hat die Höhe h = 8 cm. Berechnen Sie die Seitenlänge und die Oberfläche des Tetraeders.