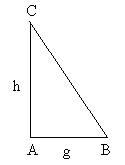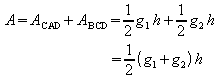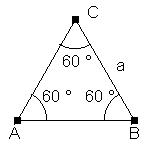
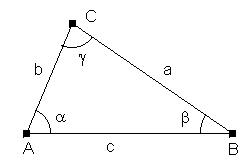
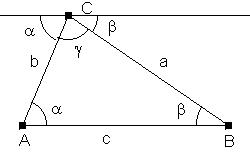
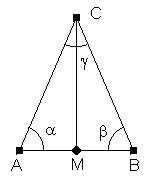
Drei Punkte in der Ebene, die nicht auf einer Geraden liegen, definieren ein Dreieck.
Wenn nichts vorgegeben ist, werden die Eckpunkte oft mit A, B, C bezeichnet. Die den Eckpunkten gegenüberliegenden Seiten werden mit a, b, c benannt. Die Winkel werden nach den Scheitelpunkten mit griechischen Buchstaben bezeichnet: a, b, g.
Für die Summe der Innenwinkel eines Dreiecks gilt: a + b + g = 180°. Dies ist leicht zu sehen, wenn durch den Eckpunkt C eine Parallele zur Seite c gezogen wird. Die Seiten b und c schneiden die beiden Parallelen, so dass a und b als Wechselwinkel an C auftreten. Mit g ergänzen die drei Winkel sich zu einem gestreckten Winkel.
Dreiecke können nach verschiedenen Merkmalen sortiert werden. Betrachtet man die Winkel, so ergibt sich eine Einteilung in * spitzwinklige Dreiecke * rechtwinklige Dreiecke * stumpfwinklige Dreiecke Bei rechtwinkligen Dreiecken werden folgende Bezeichnungen verwendet. Der rechte Winkel liege am Eckpunkt C, also g = 90°. Die dem rechten Winkel gegenüberliegende Seite (hier also c) heißt Hypotenuse, die beiden anderen Seiten, welche die Schenkel des rechten Winkels bilden, werden Katheten genannt. Für die Winkelsumme folgt: a + b + 90° = 180° , also: a + b = 90° .
Rechtwinklige Dreiecke lassen sich leicht konstruieren nach dem *Satz des Thales:* Istder Durchmesser eines Kreises und liegt der Punkt C auf diesem Kreis, so hat das Dreieck ABC bei C einen rechten Winkel. Es gilt auch die *Umkehrung:* Ist das Dreieck ABC bei C rechtwinklig, so liegt C auf einem Halbkreis mit dem Durchmesser.
Unterscheidet man Dreiecke nach Seiten, so ergibt sich die Einteilung in * allgemeine Dreiecke * gleichschenklige Dreiecke * gleichseitige Dreiecke.
Bei einem gleichschenkligen Dreieck sind zwei Seiten des Dreiecks (also die zwei Schenkel eines Winkels) gleich lang. Die dritte Seite wird Basis genannt. Die Winkel, die die Basis als einen Schenkel besitzen, heißen daher Basiswinkel. Die Basiswinkel im gleichschenkligen Dreieck sind gleich groß: a = b.
Bei einem gleichseitigen Dreieck sind alle drei Seiten gleich lang. Da ein gleichseitiges Dreieck ein spezielles gleichschenkliges Dreieck ist, müssen nach dem Basiswinkelsatz jeweils zwei Winkel gleich groß sein: a = b, b = g, g = a , also: a = b = g = 60°.
Bestimmte Geraden und Strecken haben in Dreiecken besondere Bedeutung. Diese werden unter dem Begriff Dreieckslinien zusammengefasst.
Eine Mittelsenkrechte ist eine Gerade, die senkrecht auf einer Dreieckseite steht und durch den Mittelpunkt der Seite verläuft. Die Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt. Dies ist der Mittelpunkt des Umkreises des Dreiecks, also des Kreises, auf dem die Eckpunkte des Dreiecks liegen.
Eine Winkelhalbierende ist eine Gerade, die einen Winkel halbiert (überraschend, nicht wahr?). Die Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt. Dies ist der Mittelpunkt des Inkreises des Dreiecks, also des Kreises, der im Innern des Dreiecks liegt und die Seiten in jeweils einem Punkt berührt.
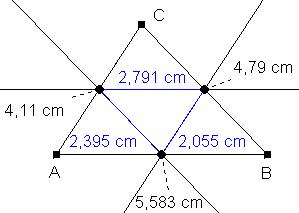
Eine Mittellinie ist eine Gerade, die durch die Mittelpunkte zweier Seiten des Dreiecks verläuft. Die Mittellinien im Dreieck sind parallel zu den gegenüberliegenden Seiten des Dreiecks und halb so lang wie diese. Die Mittellinien unterteilen das Dreieck in 4 kongruente (deckungsgleiche) Teildreiecke.
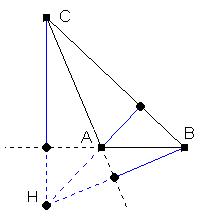
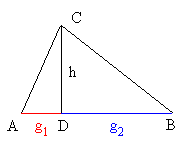
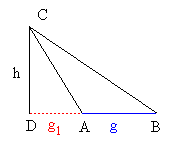
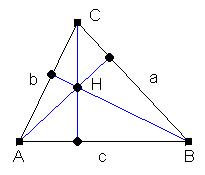
Eine Höhe im Dreieck ist eine Senkrechte auf einer Dreieckseite, die durch den gegenüberliegenden Eckpunkt verläuft. Im rechtwinkligen Dreieck fallen zwei der drei Höhen mit den Katheten zusammen. Im stumpfwinkligen Dreieck verlaufen zwei Höhen außerhalb des Dreiecks. Zu ihrer Konstruktion werden die entsprechenden Dreieckseiten verlängert und die Senkrechten auf den Verlängerungen durch die gegenüberliegenden Eckpunkte gezeichnet. Die Höhen im Dreieck schneiden sich in einem Punkt (Höhenschnittpunkt).
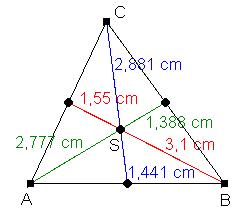
Eine Seitenhalbierende verbindet einen Eckpunkt des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite. Die Seitenhalbierenden im Dreieck schneiden sich in einem Punkt. Dies ist der Schwerpunkt S des Dreiecks. Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis 1:2.

1) Konstruieren Sie mit dem Satz des Thales ein rechtwinkliges Dreieck mit der Hypotenusenlänge c = 7 cm und der Kathetenlänge b = 4 cm.

Flächeninhalt des Dreiecks :
Ein rechtwinkliges Dreieck lässt sich als ein halbes Rechteck auffassen. Sein Flächeninhalt ist also . g steht dabei für „Grundseite“, h ist die Höhe auf der Grundseite.
Die Berechnung des Flächeninhalts eines nicht-rechtwinkligen Dreiecks wird auf das rechtwinklige Dreieck zurückgeführt. Die Höhe h zerlegt das Dreieck ABC in zwei rechtwinklige Dreiecke CAD und BCD. Damit ergibt sich: also auch hier: .
Wenn die Höhe außerhalb des Dreiecks verläuft, kann entsprechend vorgegangen werden: also wieder: .

2. Dreiecke