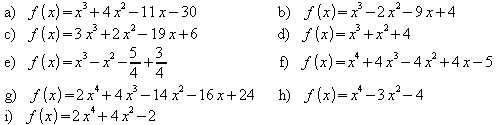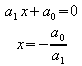 .
.
Für ganzrationale Funktionen kann in manchen Fällen ein Verfahren angegeben werden, mit dem man die Nullstellen berechnen kann. Diese Fälle sollen hier betrachtet werden.
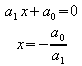 .
.
![]() .
.
Nach Division durch a2 ergibt sich die Normalform, die mit quadratischer Ergänzung weiter umgeformt wird.
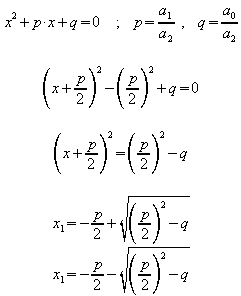
Das Vorzeichen der Diskriminante![]() bestimmt
die Lösungsmenge:
bestimmt
die Lösungsmenge:
D < 0: Es gibt keine reelle Lösung.
D = 0: Es gibt genau eine reelle Lösung:
![]()
D > 0: Es gibt zwei verschiedene reelle Lösungen x1, x2, nämlich

Es sei an den Satz von Vieta erinnert:
Zwei reelle Zahlen x1 und x2
sind genau dann Lösungen der quadratischen Gleichung in Normalform ![]() ,
wenn gilt:
,
wenn gilt: ![]() .
.
Daraus lässt folgern:
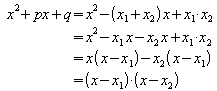
Beispiel:
![]()
Nullstellen von f sind die Lösungen der Gleichung
![]() ,
,
also
![]() .
.
Aus dem Satz von Vieta kann gefolgert werden:
![]() .
.
Es kann also der quadratische Term in ein Produkt aus linearen Termen zerlegt werden. Diese linearen Terme nennt man auch Linearfaktoren.
Es kann auch geschrieben werden:
![]()
![]() .
.
Ein Produkt nimmt den Wert Null an, wenn mindestens einer der Faktoren Null wird, hier also:
![]() .
.
Die Nullstelle x = 0 ist unmittelbar abzulesen. Mögliche weitere Nullstellen ergeben sich als Lösungen der quadratischen Gleichung.
Beispiel:
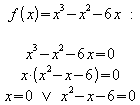
Die quadratische Gleichung hat die Lösungen
![]() .
.
Nach dem Satz von Vieta kann man schreiben:
![]() ,
,
und damit kann der Funktionsterm von f auch als Produkt aus Linearfaktoren geschrieben werden:
![]() .
.
Für den Spezialfall, dass alle Koeffizienten
ai ganzzahlig sind, kann man folgenden Satz anwenden.
| Satz: Sei f eine ganzrationale Funktion mit ganzzahligen Koeffizienten. Dann sind alle von Null verschiedenen ganzzahligen Nullstellen von f Teiler des konstanten Gliedes a0. |
Beweis:
Sei![]() eine ganzrationale Funktion vom Grad n und x0
eine ganzzahlige Nullstelle. Dann gilt:
eine ganzrationale Funktion vom Grad n und x0
eine ganzzahlige Nullstelle. Dann gilt:
![]() .
.
Ausklammern von x0 liefert:
![]() ,
,
also:
![]() .
.
Da
x0 und alle Koeffizienten
ganzzahlig sind, ist auch![]() ganzzahlig, also ist x0 ein Teiler von a0.
ganzzahlig, also ist x0 ein Teiler von a0.
Die Umkehrung des Satzes gilt nicht: Die Teiler von a0 sind nicht unbedingt Nullstelle von f, wie folgendes einfaches Beispiel klar macht: f (x) = 2x + 16. Die Koeffizienten sind ganzzahlig; die Teiler von a0 = 16 sind 2; -2; 4; -4; 8; -8; 16; -16. Lediglich -8 ist Nullstelle von f.
Beispiel:![]()
Teiler von a0 = 3 sind: -3; -1; 1; 3.
f (-3) = -27 + 9 + 15 + 3 = 0
f (-1) = -1 + 1 + 5 + 3 = 8
f (1) = 1 + 1 – 5 + 3 = 0
f (3) = 27 + 9 – 15 + 3 = 24
Nullstellen von f sind also x = -3 und x = 1.
Damit sind im allgemeinen aber noch nicht alle Nullstellen erfasst. Es ist daher nötig, den folgenden Schritt auszuführen.
2. Abspalten eines Linearfaktors (x – x0)
Beispiel 1: ![]()
Probieren: alle Koeffizienten sind ganzzahlig;
2 ist ein Teiler von 6;
f (2) = 8 – 24 + 22 – 6 = 0, also
eine Nullstelle ist x = 2.
Es wird nun versucht, f in der Form
![]()
zu schreiben. Der zunächst unbekannte Term g(x) muss ein Polynom vom Grad 2 sein. Formal ergibt er sich durch Division:
![]() .
.
Die Division eines Polynoms durch einen Linearfaktor heißt Polynomdivision. Bei dieser wird genauso vorgegangen wie bei der schriftlichen Division von Zahlen in der folgenden Form:
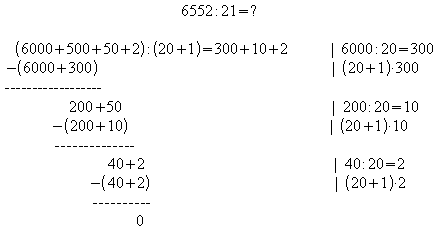
Entsprechend bei der Polynomdivision:
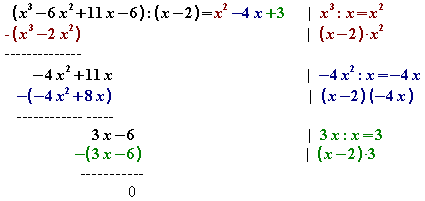
Dies führt also zu der Funktion g(x) = x2 – 4x + 3. Weitere Nullstellen von f – wenn es noch welche gibt – müssen dann Nullstellen von g sein. Um diese zu ermitteln ist nur noch eine quadratische Gleichung zu lösen:
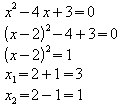
f besitzt also noch zwei weitere Nullstellen: x = 1 und x = 3 und kann daher wie folgt faktorisiert werden:
![]() .
.
Beispiel 2: ![]()
Probieren: Alle Koeffizienten sind ganzzahlig.Die Teiler von a0 = 2 sind 1; -1; 2; -2.
f (1) = 1 – 3 + 2 = 0
f (-1) = -1 + 3 + 2 = 4
f (2) = 8 – 6 + 2 = 4
f (-2) = -8 + 6 + 2 = 0
Eine Nullstelle von f ist somit x = 1; eine weitere ist x = -2.
Abspalten des Linearfaktors (x – 1): Zu beachten ist, dass im Funktionsterm ein Glied mit x2 „fehlt“:
das bedeutet, dass a2 = 0 ist.
Polynomdivision:
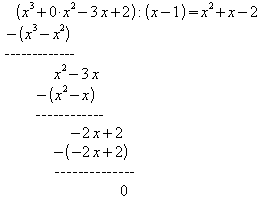
Weitere Nullstellen von f sind daher Lösungen der quadratischen Gleichung
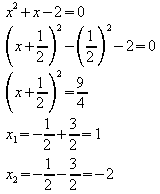
Diese beiden Nullstellen waren schon bekannt – es gibt also keine weiteren. Die faktorisierte Form von f ist
![]() .
.
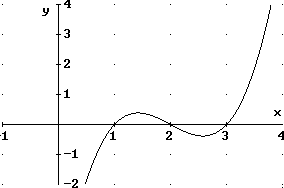
x = 1 ist eine sogenannte „doppelte Nullstelle“. Hier schneidet der Graph von f die x-Achse nicht sondern berührt sie nur.
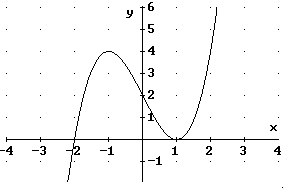
![]() .
.
Die Substitution z = x2 führt dann auf eine quadratische Gleichung:
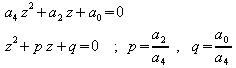 .
.
Wenn diese Gleichung Lösungen besitzt, müssen diese dann noch re-substituiert werden.
Beispiel:![]()
Substitution: z = x2
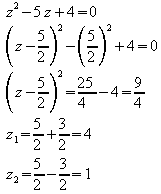
Umkehrung der Substitution: ![]() :
:
![]()
Die faktorisierte Form von f ist daher
![]() .
.
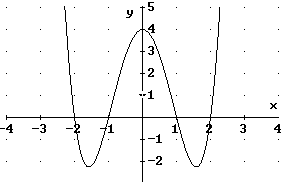
Bei diesem Beispiel wäre man auch mit „Probieren“ zum Ziel gekommen: Alle Koeffizienten sind ganzzahlig. Teiler von a0 = 4 sind 1; -1; 2; -2; 4; -4.
f (1) = 1 – 5 + 4 = 0
f (-1) = 1 – 5 + 4 = 0
f (2) = 16 – 20 + 4 = 0
f (-2) = 16 – 20 + 4 = 0
![]()
Damit ist x = 0 als eine Nullstelle bekannt.
Zur Berechnung weiterer Nullstellen ist das Problem jetzt insofern vereinfacht
worden, dass nur noch eine ganze rationale Funktion vom Grad 3 zu untersuchen
ist.
Ganzrationale Funktion vom Grad 4: f(x) = a4x4
+ a3 x3 + a2 x2
+ a1 x + a0
Probieren: f (1) = 1 – 4 – 13 + 4 + 12 = 0
Abspalten des Linearfaktors (x – 1) durch Polynomdivision:
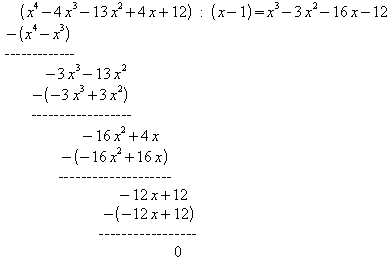
Die Restfunktion ist nur noch vom Grad 3: ![]()
Probieren zeigt: g(-1) = -1 – 3 + 16 – 12 = 0
Abspalten des Linearfaktors (x - (-1)) = (x + 1) durch Polynomdivision:
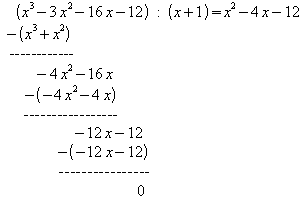
Die Restfunktion h ist vom Grad 2:![]()
Diese besitzt zwei Nullstellen: x = –2 und x = 6.
Insgesamt sind für f jetzt 4 Nullstellen gefunden worden, so dass f in faktorisierter Form geschrieben werden kann:
![]() .
.
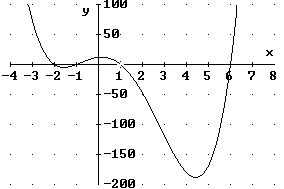
Übungen:
1. Versuchen Sie, eine oder mehrere Nullstellen der Funktion f durch Probieren zu finden.
![]()
2. Zeigen Sie, dass x0
eine Nullstelle der Funktion f ist und schreiben Sie f (x)
in der Form ![]() .
.
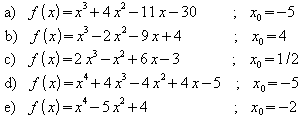
3. Wo schneidet der Graph von f die x-Achse?
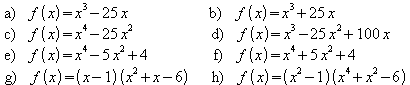
4. Bestimmen Sie die Nullstellen der Funktion f .