5.4 Die allgemeine quadratische Funktion

Die allgemeine quadratische Funktion hat die Form

Die reellen Zahlen a, b, c heißen die Koeffizienten des quadratischen Terms. Bisher wurden diejenigen quadratischen Funktionen näher betrachtet, bei denen a = 1 war. Jetzt soll der Fall mit a ¹ 1 betrachtet werden. Dabei werden zunächst b = 0 und c = 0 gesetzt.

 Die Abbildung zeigt die Graphen von.

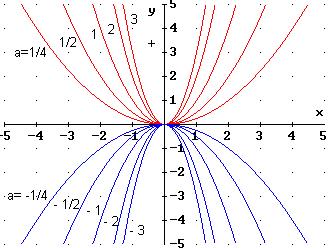
Durch Vergleich mit der Normalparabel ergibt sich:

• für a > 0 ist die Parabel nach oben geöffnet,
• für a < 0 ist die Parabel nach unten geöffnet,
• für |a| > 1 ist die Parabel enger als die Normalparabel,
• für |a| < 1 ist die Parabel weiter als die Normalparabel.

Die Verschiebung solcher Parabeln soll am Beispieluntersucht werden.

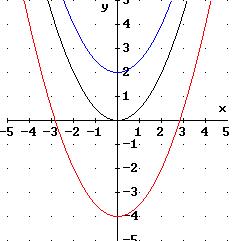
Die blaue Parabel mit dem Scheitelpunkt S = (0 ; 2) ist parallel zur y-Achse um 2 nach oben verschoben. An jeder Stelle x ist der Funktionswert der zugehörigen quadratischen Funktion g um 2 größer als der Funktionswert von, d.h. g(x) = f (x) + 2. Die verschobene Parabel ist daher der Graph der Funktion . Die rote Parabel mit dem Scheitelpunkt S = (0 ; -4) ist parallel zur y-Achse um 4 nach unten verschoben. An jeder Stelle x ist der Funktionswert der zugehörigen quadratischen Funktion h um 4 kleiner als der Funktionswert von, d.h. h(x) = f (x) - 4. Die verschobene Normalparabel ist daher der Graph der Funktion .

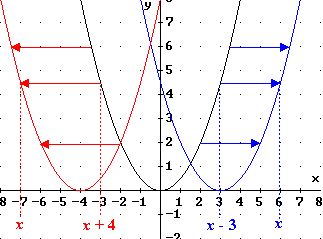
Die blaue Parabel mit dem Scheitelpunkt S = (3 ; 0) ist parallel zur x-Achse um 3 nach rechts verschoben. Der Funktionswert von g an der Stelle x ist gleich dem Funktionswert von f an der Stelle x – 3. Es gilt also. Die verschobene Parabel ist der Graph der Funktion . Die rote Parabel mit dem Scheitelpunkt S = (-4 ; 0) ist parallel zur x-Achse um 4 nach links verschoben. Der Funktionswert von h an der Stelle x ist gleich dem Funktionswert von f an der Stelle x + 4. Es gilt also. Die verschobene Parabel ist der Graph der Funktion .

Werden zwei Verschiebungen gleichzeitig vorgenommen, z.B.

• parallel zur x-Achse um 3 nach rechts,
• parallel zur y-Achse um 2 nach oben,

so entsteht eine Parabel, die der Graph der Funktionist.

In Verallgemeinerung des Beispiels gilt:

Die verschobene Parabel mit dem Scheitelpunkt S = (u ; v) ist der Graph von

Damit ist der Funktionsterm für alle Funktionen angegeben, deren Graphen verschobene Parabeln sind.

Der Graph einer quadratischen Funktion ist eine verschobene Parabel mit dem Scheitelpunkt S = (u ; v). Diese Darstellung einer quadratischen Funktion wird wie im Fall a = 1 als Scheitelpunktsform bezeichnet, weil man aus ihr die Koordinaten des Scheitelpunktes sofort ablesen kann.

Jede quadratische Funktionkann durch quadratische Ergänzung auf die Scheitelpunktsform gebracht werden.

Beispiel 1:

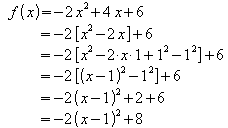
Dies ist die Scheitelpunktsform von f. Der Scheitelpunkt ist S =(1 ; 8).

Beispiel 2:

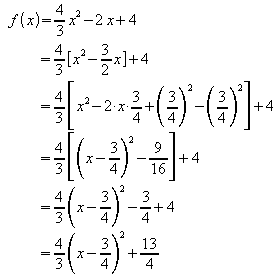
Der Scheitelpunkt ist also.

Übung:

Bestimmen Sie den Scheitelpunkt der zugehörigen Parabel.

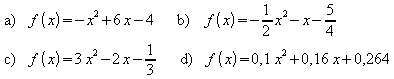
Der folgende Link verweist auf einen interaktiven Test des Projektes

        mathe-online.

Er wird außerhalb meiner Seitenstruktur in einem eigenen Browser-Fenster dargestellt.

Das große Graphen-Puzzle