5.3 Verschobene Normalparabeln

Zur Vorbereitung auf das Folgende starten Sie zunächst ein Applet, mit dem Sie Parabeln zeichnen können. Allerdings ist der Funktionsterm in einer anderen Form angegeben als bisher:

f (x) = a(x - u)² + v.

Geben Sie für a, u und v verschiedene Werte ein und versuchen Sie die Bedeutung dieser drei Parameter herauszufinden.

5.3.1 Verschiebung parallel zur y-Achse

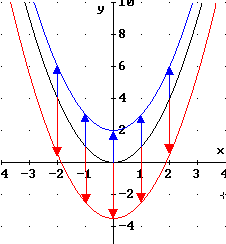
Die blaue Parabel mit dem Scheitelpunkt S = (0 ; 2) ist parallel zur y-Achse um 2 nach oben verschoben. An jeder Stelle x ist der Funktionswert der zugehörigen quadratischen Funktion g um 2 größer als der Funktionswert von f (x) = x2, d.h. g(x) = f (x) + 2. Die verschobene Normalparabel ist daher der Graph der Funktion 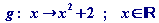. Die rote Parabel mit dem Scheitelpunkt S = (0 ; -3,5) ist parallel zur y-Achse um 3,5 nach unten verschoben. An jeder Stelle x ist der Funktionswert der zugehörigen quadratischen Funktion h um 3,5 kleiner als der Funktionswert von f (x) =  x2 , d.h. h(x) = f (x) -3,5. Die verschobene Normalparabel ist daher der Graph der Funktion .

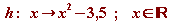Allgemein gilt:
 

Die verschobene Normalparabel mit dem Scheitelpunkt S = (0 ; v) ist der Graph der Funktion 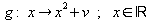 . Ist v > 0, so ist die Normalparabel nach oben verschoben. Ist v < 0, so ist die Normalparabel nach unten verschoben.

5.3.2 Verschiebung parallel zur x-Achse

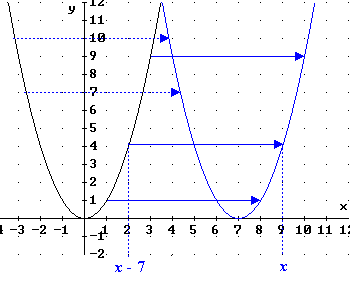
Die blaue Parabel mit dem Scheitelpunkt S = (7 ; 0) ist parallel zur x-Achse um 7 nach rechts verschoben.  g sei die zugehörige quadratische Funktion und f (x) = x2. Es ist abzulesen:  g(7) = f (0) = 0  g(8) = f (1) = 1  g(9) = f (2) = 4  g(10) = f (3) = 9  g(6) = f (-1) = 1  g(5) = f (-2) = 4  g(4) = f (-3) = 9  Der Funktionswert von g an der Stelle x ist gleich dem Funktionswert von f an der Stelle x – 7. Es gilt also g(x) = f (x – 7) = (x – 7)2. Die verschobene Normalparabel ist der Graph der Funktion .

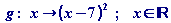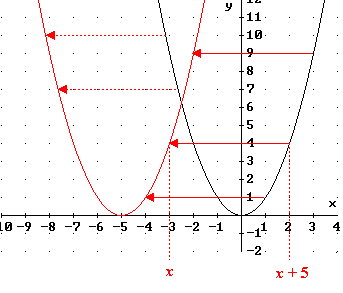
Die rote Parabel mit dem Scheitelpunkt S = (-5 ; 0) ist parallel zur x-Achse um 5 nach links verschoben.  h sei die zugehörige quadratische Funktion und f (x) = x2. Es ist abzulesen:  h(-5) = f (0) = 0  h(-4) = f (1) = 1  h(-3) = f (2) = 4  h(-2) = f (3) = 9  h(-6) = f (-1) = 1  h(-7) = f (-2) = 4  h(-8) = f (-3) = 9 Der Funktionswert von h an der Stelle x ist gleich dem Funktionswert von f an der Stelle x + 5. Es gilt also h(x) = f (x + 5) = (x + 5)2 = (x - (-5))2. Die verschobene Normalparabel ist der Graph der Funktion

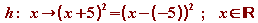
Allgemein gilt:
 

Die verschobene Normalparabel mit dem Scheitelpunkt S = (u ; 0) ist der Graph der Funktion 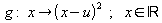 . Ist u > 0, so ist die Normalparabel nach rechts verschoben. Ist u < 0, so ist die Normalparabel nach links verschoben.

5.3.3 Verschiebung parallel zur x-Achse und zur y-Achse

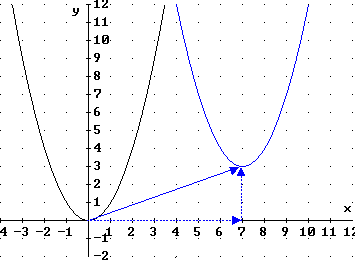
Die blaue Parabel mit dem Scheitelpunkt S = (7 ; 3) ist parallel zur x-Achse um 7 nach rechts und dann parallel zur y-Achse um 3 nach oben verschoben. Die verschobene Normalparabel ist daher der Graph der Funktion .

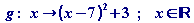Allgemein gilt:

Die verschobene Normalparabel mit dem Scheitelpunkt S = (u ; v) ist der Graph von

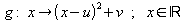Damit ist der Funktionsterm für alle Funktionen angegeben, deren Graphen verschobene Normalparabeln sind.

Der Graph einer quadratischen Funktion 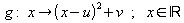ist eine verschobene Normalparabel mit dem Scheitelpunkt S = (u ; v). Man nennt diese Darstellung einer quadratischen Funktion die Scheitelpunktsform, weil man aus ihr die Koordinaten des Scheitelpunktes sofort ablesen kann.

Übung:

Bestimmen Sie zu den verschobenen Normalparabeln mit den angegebenen Scheitelpunkten jeweils den Funktionsterm.

a) (3 ; 4)    b) (-1 ; 5)    c) (2 ; -3)    d) (-1 ; -1)    e) (-3 ; -8)    f) (0,4 ; -1,2)

5.3.4 Herstellen der Scheitelpunktsform

Jede quadratische Funktion, die in der Normalform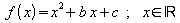gegeben ist, lässt sich in Scheitelpunktsform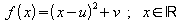darstellen.

Beispiel 1:

a)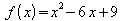 

Der Funktionsterm lässt sich nach der zweiten binomischen Formel als Quadrat schreiben:

.

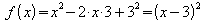Dies ist die Scheitelpunktsform von f , und der Scheitelpunkt ist S = (3 ; 0).

b)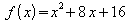 

Der Funktionsterm lässt sich nach der ersten binomischen Formel als Quadrat schreiben:

.

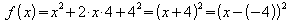Dies ist die Scheitelpunktsform von f , und der Scheitelpunkt ist S = (- 4; 0).

Beispiel 2:

a)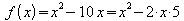 

Dieser Term ist kein vollständiges Quadrat, denn es fehlt das quadratische Glied 5². Man kann es jedoch in der Form 5² – 5² hinzufügen:

.

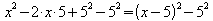Die Scheitelpunktsform von f lautet also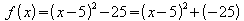. Der Scheitelpunkt ist S = (5 ; -25).

b)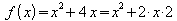 

Hier fehlt zum vollständigen Quadrat das quadratische Glied 2². Es wird in der Form 2² – 2² hinzugefügt:

.

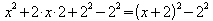Die Scheitelpunktsform von f lautet also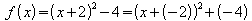. Der Scheitelpunkt ist S = (- 2; - 4).

Das fehlende quadratische Glied, das bei diesem Verfahren ergänzt wird, nennt man quadratische Ergänzung.

Beispiel 3:

a)

 

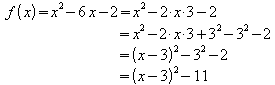
Die Scheitelpunktsform von f lautet also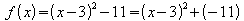. Der Scheitelpunkt ist S = (3 ; -11).

b)

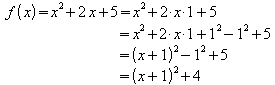
Die Scheitelpunktsform von f lautet also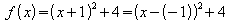. Der Scheitelpunkt ist S = (-1 ; 4).

Übungen:

1. Formen Sie um wie in den Beispielen.

.
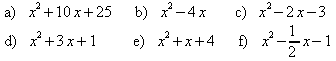    (Zur Kontrolle können Sie die Graphen mit dem Applet aus Abschnitt 1 zeichnen und die Scheitelpunkte ablesen.)

2. Eine verschobene Normalparabel hat den Scheitelpunkt S. Bestimmen Sie die Scheitelpunktsform der zugehörigen quadratischen Funktion.

    a) S = (0 ; 2,5)     b) S = (4 ; 0)     c) S = (-1,5 ; 0)     d) S = (0 ; -3)     e) S = (1 ; 2)

     f) S = (-2 ; 3,5)    g) S = (3 ; -4)   h) S = (-1 ; 3)         i) S = (-1 ; -2,5)

    (Kontrollmöglichkeit: Benutzen Sie das Applet vom Anfang dieser Seite, um die Parabeln zeichnen zu lassen.)

3. Der Graph einer quadratischen Funktio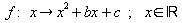nhat den Scheitelpunkt S. Bestimmen Sie b und c und geben Sie den Funktionsterm an.

    a) S = (0,5; 2,5)     b) S = (-1 ; 1,5)     c) S = (-0,5 ; - 2,5)

    d) S = (- 4 ; 1)        e) S = (1,5 ; -2)     f) S = (0,5 ; 0,5)

    (Kontrollmöglichkeit: Benutzen Sie das Applet aus Abschnitt 1, lassen Sie die Parabeln zeichnen und prüfen Sie, ob die Parabeln den vorgegebenen Scheitelpunkt besitzen.)
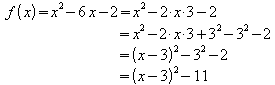
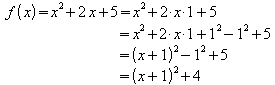
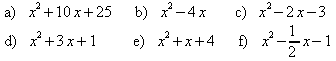