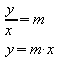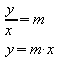3. Ursprungsgeraden

Proportionale Zuordnungen sind Funktionen, deren Graphen Ursprungsgeraden sind, d.h. sie verlaufen durch den Koordinatenursprung.Die Gleichungwird daher auch als Geradengleichung bezeichnet. Die Funktion, deren Graph diese Gerade ist, wird mitoderbeschrieben.

Beispiele:
 

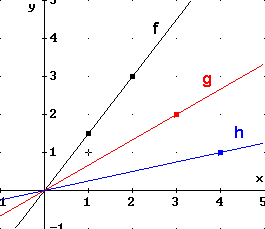
Bei der mit f gekennzeichneten Geraden ist abzulesen: und , also: . Es handelt sich um den Graphen der Funktion . Die beiden anderen Geraden sind die Graphen der Funktionen  und .

2. Um Ursprungsgeraden zu zeichnen, braucht man nur einen Punkt P(x ; y) zu ermitteln, der auf der Geraden liegt. Dazu kann ein beliebiger Wert für x gewählt und in die Geradengleichung eingesetzt werden. Es ergibt sich dann die y-Koordinate des Geradenpunktes. Die Gerade verläuft dann durch diesen Punkt und den Koordinatenursprung. Beispiele:
 

: für x = 2 ergibt sich , also ist P(2;1) ein Punkt der Geraden.   : für x = 3 ergibt sich ,  also ist P(3;6) ein Punkt der Geraden.

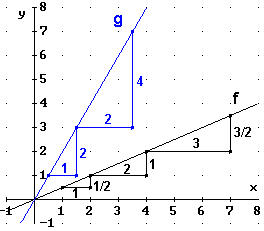Für f gilt:
Vergrößert man x um 1, dann vergrößert sich der Funktionswert um.

Beim Graphen von f bedeutet das:

Geht man von einem Punkt der Geraden aus um 1 nach rechts, so muss man umnach oben gehen, um wieder auf der Geraden zu landen.

Entsprechend gilt für f :

Vergrößert man x um , so vergrößert sich der Funktionswert um .

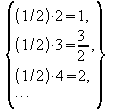Für den Graphen bedeutet das:

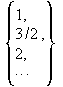Geht man von einem Punkt der Geraden aus um  nach rechts, so muss man umnach oben gehen, um wieder auf der Geraden zu landen.

Für g gilt:

Vergrößert man x um , so vergrößert sich der Funktionswert um .

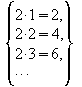Für den Graphen bedeutet das:

Geht man von einem Punkt der Geraden aus um  nach rechts, so muss man umnach oben gehen, um wieder auf der Geraden zu landen.

Inbzw.heißt m die Steigung der Geraden. Dreiecke, wie die in der Abbildung eingezeichneten, nennt man Steigungsdreiecke.
 

3. Wenn eine Ursprungsgerade in graphischer Form vorliegt, so kann ihre Steigung m wie folgt bestimmt werden:
 

Zeichnen eines Steigungsdreiecks, Ablesen der Seitenlängen, Berechnen der Steigung  Die Steigung kann direkt abgelesen werden, wenn ein Steigungsdreieck mitgewählt wird.

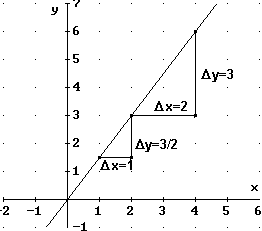Für das abgebildete Beispiel erhält man:

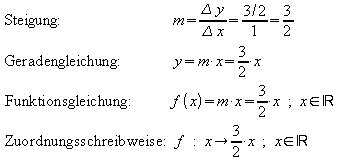
4. Die bisher betrachteten Beispiele zeigten steigende Geraden. Der Begriff „steigen“ ist so zu verstehen, dass bei größer werdendem x-Wert auch die y-Werte größer werden. In diesem Fall ist die Steigung m der Geraden positiv.
 

Nun kann eine Gerade sich aber auch so verhalten, dass bei größer werdenden x-Werten die y-Werte kleiner werden. Dann handelt es sich um eine fallende Gerade. Im abgebildeten Beispiel ist abzulesen, dass bei einer Zunahme von x umdie y-Werte um 2 kleiner werden; dies ist durch ein negatives Vorzeichen zu berücksichtigen:. Daraus ergibt sich, dass eine fallende Gerade eine negative Steigung besitzt.

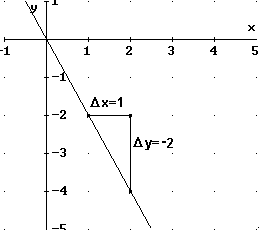5. Zeichnen einer Ursprungsgeraden bei gegebener Geradengleichung

a) mit zwei Punkten
 

Beispiel:.  Außer dem Ursprung P(0;0) benötigt man noch einen zweiten Punkt, durch den die Gerade verläuft. Dazu kann ein im Prinzip beliebiger Wert für x gewählt und in die Geradengleichung eingesetzt werden; der damit berechnete y-Wert ist die y-Koordinate des Punktes Q(x ; y) auf der Geraden.  x = 5: , also: Q = (5;4)

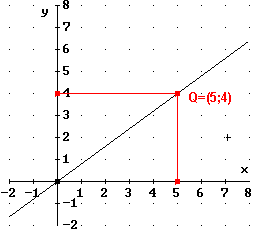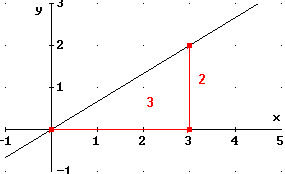
b) mit der Steigung
 

Beispiel: . Hierbei geht man vom Koordinatenursprung um x Einheiten nach rechts, und von dort aus um  Einheiten nach oben (falls m > 0) bzw. nach unten (falls m < 0). Geht man im betrachteten Beispiel also 3 Einheiten nach rechts, so muss von dort dann um  Einheiten nach oben gegangen werden.

Übungen:

1. Zeichnen Sie mit Hilfe des Ursprungs und der Steigung den Graphen von f.

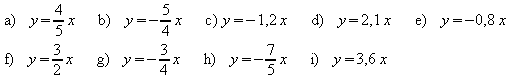
2. Zeichnen Sie eine Ursprungsgerade durch P. Tragen Sie ein Steigungsdreieck ein und bestimmen Sie die Steigung. Wie heißt die zugehörige Geradengleichung?

a) P(1 ; 2) b) P(3 ; 6) c) P(2 ; 8) d) P(-1 ; 1) e) P(-4 ; 4) f) P(2,5 ; -5)

3. Die folgenden Punkte liegen auf einer Ursprungsgeraden. Geben Sie (ohne zu rechnen) an, ob die Steigung der Geraden größer, kleiner oder gleich Null ist.

a) P(-7 ; 1) b) P(-1 ; 4) c) P(1 ; 3) d) P(-1 ; -2) e) P(3 ; 8) f) P(1 ; 0)

4. Untersuchen Sie, ob die beiden Punkte P₁ und P₂ auf einer Ursprungsgeraden y = mx liegen.

a) P₁(-1 ; -3) , P₂(1 ; 3) b) P₁(4 ; -1) , P₂(2 ; -2) c) P₁(1,5 ; 3) , P₂(4,5 ; -9)

d) P₁(-1,5 ; -3) , P₂(4,5 ; 9) e) P₁(2;5,5) , P₂(1 ; 2,25) f) P₁(3,1 ; -6) , P₂(3,1 ; 6)

Der folgende Link verweist auf eine interaktive Übung des Projektes
        mathe-online.

Steigung einer Geraden