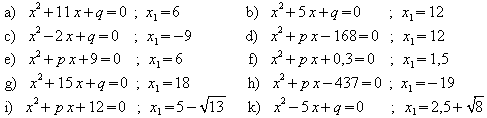4.3 Der Satz von Viëta

Der Satz von Viëta (François Viète, lateinisiert Viëta. 1540 – 1603) ist ein nützliches Hilfsmittel 1) Beispiel: Die Lösungsmenge soll  sein. Offensichtlich sind 3 und –2 Lösungen der Gleichung

;

denn der erste Faktor wird Null, wenn 3 für x eingesetzt wird, und der zweite Faktor wird Null, wenn -2 für x eingesetzt wird.

Durch Ausmultiplizieren ergibt sich die Normalform:

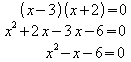
2) In Verallgemeinerung des Beispiels ergibt sich: Die Lösungsmenge soll  sein. Dies sind Lösungen der Gleichung

.

Die Gleichung wird durch Ausmultiplizieren auf Normalform gebracht:

Ein Vergleich mit  zeigt, dass offensichtlich gilt: .

Damit ist eine quadratische Gleichung in Normalform gefunden, zu der die vorgegebenen Lösungsmenge passt.

3) Es soll nun gezeigt werden: Für jede lösbare quadratische Gleichung in Normalform gilt: .

Beweis: habe die beiden reellen Lösungen x1 und x2 .

Nach dem Lösungssatz gilt dann:

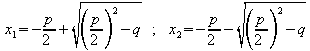
Es ist

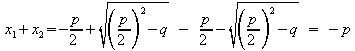
und

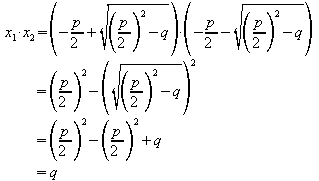
Damit ist bewiesen:
Wenn x1 und x2 die Lösungen der quadratischen Gleichung  sind, dann gilt für die Koeffizienten .

4) Von diesem Satz gilt auch die Umkehrung:
Wenn für die Koeffizienten p und q der quadratischen Gleichung  gilt: , dann sind x1 und x2 die Lösungen dieser Gleichung.

Beweis:

Einsetzen von x1 ergibt:

Einsetzen von x2 ergibt:

5) Zusammengefasst folgt der
 
Satz von Viëta:
Zwei reelle Zahlen x1 und x2 sind genau dann Lösungen der quadratischen Gleichung in Normalform , wenn gilt: .

Anwendung zum Aufstellen von Gleichungen:

Gesucht ist eine quadratische Gleichung mit der Lösungsmenge .

Es gilt ,. Die gesuchte Gleichung ist also .

Anwendung zur Probe:

a) Ist  die Lösungsmenge von ?

Die angegebene Gleichung hat also die Lösungsmenge .

b) Ist  die Lösungsmenge von ?

Anwendung zum Lösen:

Für die Lösungen von  muss gelten . Es wird 6 in zwei ganzzahlige Faktoren u und v zerlegt und –(u + v) gebildet:
 
u 1 2 -1 -2
v 6 3 -6 -3
–(u + v) -7 -5 7 5

Übungen

1. Bestimmen Sie die Lösungsmenge mit Hilfe des Satzes von Viëta.

2. Von einer quadratischen Gleichung  sind eine Lösung und einer der Koeffizienten p und q bekannt. Bestimmen Sie die zweite Lösung und den unbekannten Koeffizienten.