Bruchterme

Ein Term, der im Nenner mindestens eine Variable enthält, heißt Bruchterm.

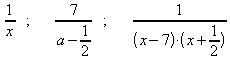
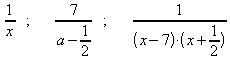
Die Menge aller rationalen Zahlen, für die der Nenner eines Bruchterms von Null verschieden ist, heißt DefinitionsmengeD des Bruchterms.
 

Bruchterm
Nullstellen des Nenners
Definitionsmenge des Bruchterms

Rechnen mit Bruchtermen

Zwei Bruchterme mit denselben Variablen und den Definitionsmengen D1 und D2 heißen gleich in, wenn sie bei jeder Einsetzung von rationalen Zahlen aus denselben Wert haben.

Erweitern und Kürzen

Beim Erweitern und Kürzen dürfen nur Terme verwendet werden, die in der Definitionsmenge des betrachteten Bruchterms nicht den Wert Null ergeben.

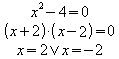1) 

2) 

Der Termbesitzt bei jeder Einsetzung rationaler Zahlen einen von Null verschiedenen Wert. Es darf also gekürzt werden.

Beim Kürzen und Erweitern eines Terms mit der Definitionsmenge D1 kann sich ein Term mit einer anderen Definitionsmenge D2 ergeben. Die Terme sind dann nur auf der gemeinsamen Definitionsmengegleich.

3) 

Der ursprüngliche Term hat die Definitionsmenge. Der Termist in dieser Menge von Null verschieden, es darf also gekürzt werden. Der nach dem Kürzen erhaltene Term hat die Definitionsmenge. Ausgangsterm und gekürzter Term sind aber nur auf der gemeinsamen Definitionsmengegleich.

4) 

Der Ausgangsterm hat die Definitionsmenge. Da mit x – 2 erweitert wird, darf x nicht den Wert 2 annehmen. Die Definitionsmenge des erweiterten Terms ist daher und die beiden Terme sind nur auf der gemeinsamen Definitionsmengegleich.

5) 

Addieren und Subtrahieren

Haben Bruchterme den gleichen Nenner, so haben sie auch die gleiche Definitionsmenge. Für solche Terme gilt:

Mit Bruchtermen rechnet man wie mit Brüchen.
Nennergleiche Bruchterme werden addiert bzw. subtrahiert, indem man die Zählerterme addiert bzw. subtrahiert und den Nennerterm beibehält.

Sind die Bruchterme nicht nennergleich, so kann man sie in der gemeinsamen Definitionsmengedurch Erweitern oder Kürzen in nennergleiche Bruchterme umwandeln und dann subtrahieren bzw. dividieren.

Den einfachsten gemeinsamen Nenner (Hauptnenner) findet man oft erst, nachdem man die Nenner der Bruchterme in Produkte umgeformt hat:

Multiplizieren und Dividieren

Bruchterme werden multipliziert, indem man die Zählerterme multipliziert und die Nennerterme multipliziert.

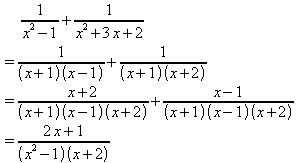
Wenn möglich sollte man vor dem Multiplizieren kürzen.

Die Division wird auf die Multiplikation zurückgeführt. Man dividiert durch einen Bruchterm, indem man mit dem „Kehrterm“ multipliziert. Der „Kehrterm“ hat in der Regel eine andere Definitionsmenge als der Term selbst, weil der Zähler zum Nenner geworden ist.

Übungen:

1. Kürzen bzw. berechnen Sie.
(Die Eingabefelder sind für Notizen gedacht. Ein Vergleich der Inhalte mit den Lösungen wird nicht durchgeführt.)
1) 
2)
3) 
4)
5) 

Lösung

2. Bruchterme: Zuordnungsübung

Der folgende Link verweist auf einen interaktiven Tests des Projektes

       mathe-online.

Er wird außerhalb meiner Seitenstruktur in einem eigenen Browser-Fenster dargestellt.

Bruchterme kürzen