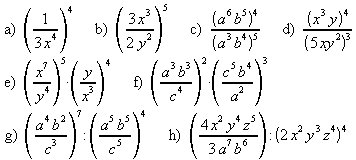1. Der Flächeninhalt eines Quadrats mit der
Seite a ist bekanntlich ![]() .
.
2. Das Volumen eines Würfels mit der Kante
a ist ![]() .
.
3. Bei der Vermehrung von Einzellern durch Zellteilung ergibt sich folgendes Bild:
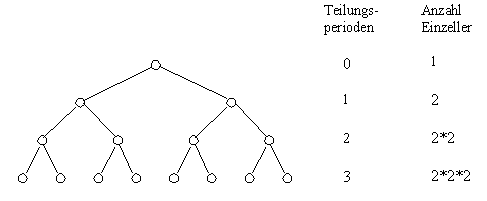
Nach n Teilungsperioden beträgt die Anzahl offensichtlich
4. Bei der jährlichen Verzinsung eines Kapitals K0 zu einem Zinssatz p% ist das Wachstum des Kapitals wie folgt zu berechnen:
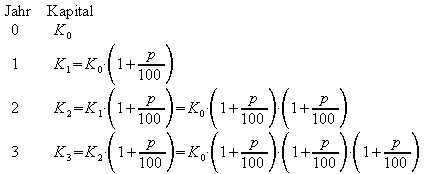
Nach n Jahren ist das Anfangskapital dann angewachsen auf
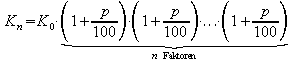 .
.
Für Produkte aus gleichen Faktoren wird die Potenzschreibweise benutzt:
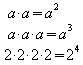
Allgemein wird definiert:
![]() .
.
Da ein Produkt mindestens zwei Faktoren hat, wurde
für die Potenz
an zunächst ![]() vorausgesetzt. Eine erste kleine Verallgemeinerung ergibt sich wie folgt:
vorausgesetzt. Eine erste kleine Verallgemeinerung ergibt sich wie folgt:
| Als Produkt geschrieben hat | |
| a3 einen Faktor weniger als a4, | |
| a2 einen Faktor weniger als a3, | |
| Führt man dieses Schema weiter,
so müsste
a1 = a sein. |
Dies wird auch so festgelegt. Damit ist ![]() definiert:
definiert:
![]() .
.
Übungen: Potenzen mit natürlichen Zahlen als Exponenten
1. Schreiben Sie als Potenz. Beispiel: ![]() .
.
![]()
2. Schreiben Sie als Zehnerpotenz. a) 100 000 b) 10 Milliarden c) 1 Billion
3. Berechnen Sie.
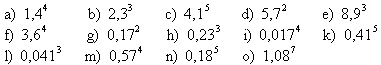
4. Ordnen Sie in einer Ungleichungskette an.
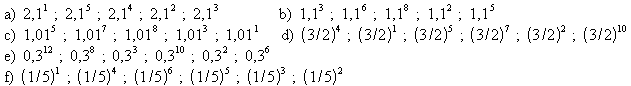
5. Berechnen Sie ohne Taschenrechner.
![]()
Die beiden letzten Übungen lassen folgende Eigenschaften von Potenzen erkennen.
Satz 1: Für Potenzen mit Exponenten
aus ![]() gilt:
gilt:
6. Ergänzen Sie wie im Beispiel: 23+1 ist das Doppelte von 23.
25+1 ist das _______________ von 25 ; 2n+1 ist das _______________ von 2n
2n+2 ist das _______________ von 2n ; 2n+3 ist das _______________ von 2n
3n+1 ist das _______________ von 3n ; 3n+2 ist das _______________ von 3n
7. Ordnen Sie der Größe nach.
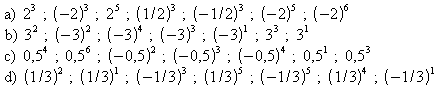
8. Welches der Zeichen <, >, = ist einzusetzen,
damit wahre Aussagen entstehen? ![]()
| Wenn | dann |
|
|
 aq
aq |
|
|
 aq
aq |
|
|
 aq
aq |
|
|
 aq
aq |
|
|
 a2p
a2p |
|
|
 a2p
a2p |
|
|
 a2p
a2p |
|
|
 a2p
a2p |
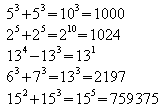
2. Vereinfachen bzw. berechnen Sie.
![]()
3. Sie kennen die Vorrangregel „Punktrechnung kommt vor Strichrechnung“. Das bedeutet, Multiplikationen und Divisionen sind vor Additionen und Subtraktionen auszuführen.
Diese Regel ist zu nun zu erweitern:
Die Rechenart Potenzieren kommt vor Punktrechnung, und Punktrechnung kommt wie bisher vor Strichrechnung.
Beispiel: In ![]() ist zuerst die Potenz auszurechnen:
ist zuerst die Potenz auszurechnen:
![]() .
.
Wenn erst die Multiplikation ausgeführt werden soll, muss die Abweichung von der Reihenfolge der Rechenarten durch Klammern erzwungen werden:
![]() .
.
Entsprechend:
![]() .
.
Übungen: Terme mit Potenzen
1. Vereinfachen Sie.
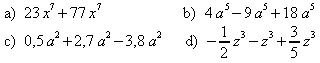
2. Vereinfachen Sie zuerst und berechnen Sie dann.
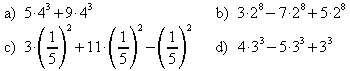
![]() .
.
Allgemein ergibt sich entsprechend:
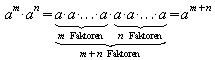 .
.
![]() für alle
für alle ![]()
Übungen: Multiplizieren von Potenzen mit gleicher Basis
1. Zerlegen Sie die Potenz auf mindestens drei Arten in zwei Faktoren.
Beispiel:![]()
![]()
2. Suchen Sie die falschen Aussagen heraus.
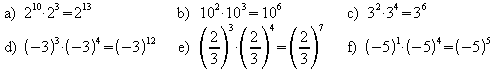
3. Schreiben Sie das Produkt als eine Potenz.
![]()
4. Vereinfachen Sie.
Beispiel:![]()
![]()
5. Schreiben Sie das Produkt als eine Potenz.
![]()
6. Vereinfachen Sie.
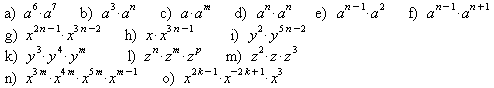
7. Klammern Sie aus und kürzen Sie ![]() .
.
Beispiel:![]()
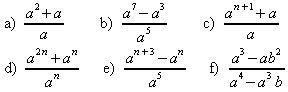
8. Multiplizieren Sie aus.
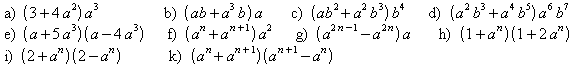
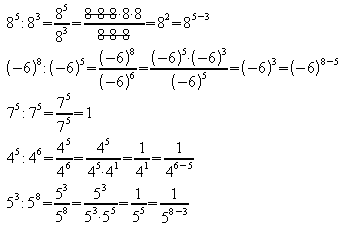
Allgemein gilt für das Dividieren von Potenzen mit gleicher Basis:
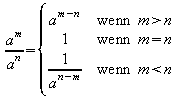 für alle
für alle ![]() .
.
Übungen: Dividieren von Potenzen mit gleicher Basis
1. Schreiben Sie als eine Potenz.
![]()
2. Kürzen Sie.
![]()
3. Schreiben Sie als eine Potenz.
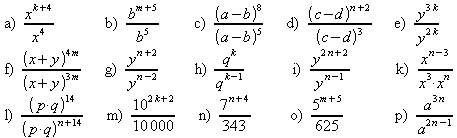
4. Welche Potenz ist in die Leerstelle einzusetzen?
![]()
5. Wie heißt der zweite Faktor?
![]()
6. Machen Sie nennergleich und vereinfachen Sie, wenn möglich.
Beispiel:![]()
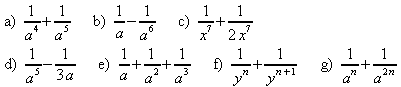
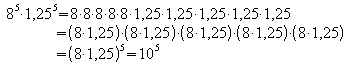
Allgemein:
![]() für alle
für alle ![]() .
.
In Worten: Potenzen mit gleichen Exponenten werden multipliziert, indem man ihre Basen multipliziert und das Produkt mit dem gemeinsamen Exponenten potenziert.
Von rechts nach links gelesen:![]() .
Ein Produkt wird potenziert, indem man jeden Faktor potenziert.
.
Ein Produkt wird potenziert, indem man jeden Faktor potenziert.
Entsprechend gilt für Quotienten von Potenzen mit gleichen Exponenten
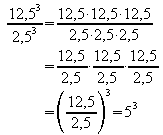
Allgemein:
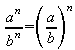 für alle
für alle ![]() .
.
In Worten: Potenzen mit gleichen Exponenten werden dividiert, indem man ihre Basen dividiert und den Quotienten mit dem gemeinsamen Exponenten potenziert.
Von rechts nach links gelesen: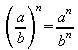 .
Ein Quotient wird potenziert, indem man Zähler und Nenner potenziert.
.
Ein Quotient wird potenziert, indem man Zähler und Nenner potenziert.
Übungen: Potenzen mit gleichen Exponenten
1. Berechnen Sie. Beispiel: ![]()
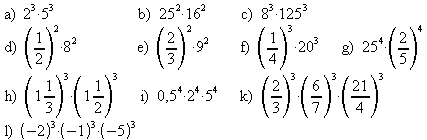
2. Potenzieren Sie das Produkt. Beispiel: ![]()
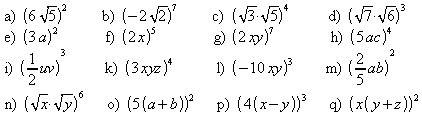
3. Schreiben Sie als eine Potenz. Beispiel: ![]()
![]()
4. Schreiben Sie als eine Potenz und vereinfachen Sie, wenn möglich.
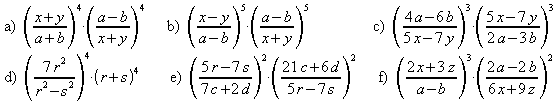
5. Berechnen Sie. Beispiel: ![]()
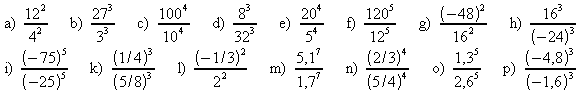
6. Potenzieren Sie den Quotienten. Beispiel: ![]()
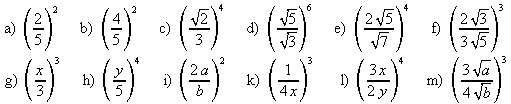
![]() .
.
Nach der Regel für die Multiplikation von Potenzen gleicher Basis gilt
![]() .
.
Also ist
![]() .
.
Allgemein gilt:
![]() für alle
für alle ![]() .
.
In Worten: Eine Potenz wird potenziert, indem man die Exponenten multipliziert und die Basis beibehält.
Übungen: Potenzieren von Potenzen
1. Berechnen Sie die Potenz. Beispiel: ![]()
![]()
2. Schreiben Sie als Potenz mit möglichst kleiner Basis.
![]()
3. Formen Sie um. Beispiel: ![]()
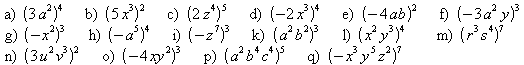
4. Formen Sie um und vereinfachen Sie, wenn möglich.