| Definition: Statt Wurzel sagt man auch Quadratwurzel, da ihr Quadrat den Radikanden ergibt. |
| Definition: Statt Wurzel sagt man auch Quadratwurzel, da ihr Quadrat den Radikanden ergibt. |
Ö9 ist diejenige positive Zahl, die mit sich selbst multipliziert 9 ergibt. Eine solche Zahl ist bekannt, nämlich 3:
Ö9 = 3, denn 32 = 9.
Es gibt aber noch eine weitere Zahl, die mit sich selbst multipliziert 9 ergibt, nämlich -3:
(-3)2 = 9.
Es ist jedoch falsch, daraus zu schließen, dass Ö9 auch -3 sein könnte, denn gemäß der Definition ist die Wurzel einer Zahl eine nicht-negative Zahl.
Entsprechend gilt:
Ö36 = 6 , denn 62 = 36 und
6 > 0 ;
Ö0,16 = 0,4 , denn 0,42 = 0,16
und 0,4 > 0 ;
Ö2,56 = 1,6 , denn 1,62 = 2,56
und 1,6 > 0.
Vergleicht man ![]()
mit ![]() ,
,
so erkennt man: ![]() .
.
Hätte man sich bei der Definition der Wurzel dagegen auf die negativen Zahlen, deren Quadrat den Radikanden ergibt, festgelegt, so würde hier gelten:
![]() ,
,
![]() ,
,
![]()
2) Besonders einfach lässt sich die Wurzel aus dem Quadrat einer Zahl ziehen:
![]()
Allgemein gilt:
![]() .
.
3) Die beiden Gleichungen ![]() haben nicht die gleiche Lösungsmenge.
haben nicht die gleiche Lösungsmenge.
| Mit der Gleichung
werden Zahlen x gesucht, deren Quadrate 16 sind. Es gibt zwei Zahlen, die diese Bedingung erfüllen: 1) die Zahl 4, denn 42 = 16, und 2) die Zahl -4, denn (-4)2 = 16. Daraus folgt L = {-4 ; 4}. |
Mit der Gleichung
werden positive Zahlen x gesucht, deren Quadrate 16 sind. Es gibt nur eine Zahl, die diese Bedingung erfüllt: die Zahl 4, denn 42 = 16 und 4 > 0.
Daraus folgt L ={4}. |
Da auch in![]() das
Distributivgesetz gilt, lassen sich Summen durch Ausklammern gelegentlich
vereinfachen:
das
Distributivgesetz gilt, lassen sich Summen durch Ausklammern gelegentlich
vereinfachen:
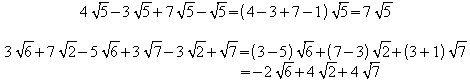
Allgemein führt das Produkt![]() zweier
Quadratwurzeln auf:
zweier
Quadratwurzeln auf:
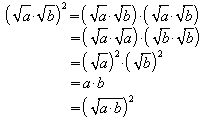
Es ergibt sich also die Gleichung
![]() .
.
Wenn aber die Quadrate zweier positiver Zahlen gleich sind, dann sind auch die beiden Zahlen selbst gleich. Also gilt:
Liest man diese Regel von rechts nach links, so ergibt sich, dass man aus einem Produkt die Wurzel ziehen kann, indem aus jedem Faktor die Wurzel gezogen wird. Dies führt zu einer weiteren nützlichen Regel für den Fall, dass man den Radikanden einer Wurzel so in ein Produkt zerlegen kann, dass ein Faktor dabei eine Quadratzahl ist. Man spricht dann vom „teilweisen Wurzelziehen“. Beispiele:
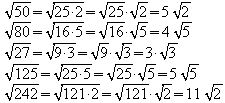
Allgemein:
Wird diese Identität von rechts nach links gelesen, so ergibt sich, dass man einen bei einer Wurzel stehenden positiven Faktor „unter die Wurzel bringen“ kann.
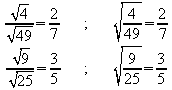
Allgemein führt der Quotient ![]() zweier Quadratwurzeln auf:
zweier Quadratwurzeln auf:
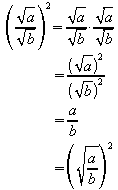
Es ergibt sich also die Gleichung
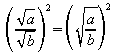 .
.Wenn aber die Quadrate zweier positiver Zahlen gleich sind, dann sind auch die beiden Zahlen selbst gleich. Also gilt:
Liest man diese Regel von rechts nach links, so ergibt sich, dass man aus einem Quotienten die Wurzel ziehen kann, indem aus Zähler und Nenner die Wurzel gezogen wird.
Wie bei Produkten von Wurzeln ergibt sich auch hier die Möglichkeit des „teilweisen Wurzelziehens“ bzw. des „unter die Wurzel bringens“ einer positiven Zahl:
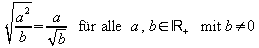 .
.Beseitigt man Wurzeln im Nenner von Wurzeltermen, so lassen sich diese oft besonders einfach und genau berechnen.
Beispiel: Die folgenden Terme sollen mit den rationalen Näherungszahlen![]() berechnet
werden.
berechnet
werden.
![]()
Mit einem Taschenrechner ergibt sich ![]() .
Mehr Stellen zeigt der TR nicht an, so dass zumindest Unsicherheit besteht,
ob dies Ergebnis der Näherungsrechnung wenigstens genau ist. Wird
die Rechnung von Hand ausgeführt, so zeigt sich, dass dies nicht der
Fall ist. Das genaue Ergebnis ist
.
Mehr Stellen zeigt der TR nicht an, so dass zumindest Unsicherheit besteht,
ob dies Ergebnis der Näherungsrechnung wenigstens genau ist. Wird
die Rechnung von Hand ausgeführt, so zeigt sich, dass dies nicht der
Fall ist. Das genaue Ergebnis ist ![]() .
.
![]()
Der TR liefert ![]() ,
also ein „genaues“ Ergebnis für die Näherungsrechnung.
,
also ein „genaues“ Ergebnis für die Näherungsrechnung.
![]()
Der TR lässt wie im Beispiel (1) wieder Unsicherheit bestehen,
ob das angezeigte Ergebnis exakt ist: ![]() .
Die Rechnung von Hand zeigt, dass dies nicht der Fall ist:
.
Die Rechnung von Hand zeigt, dass dies nicht der Fall ist:![]() .
.
Nun sollen die Terme zuerst so umgeformt werden, dass der Nenner keine Wurzeln mehr enthält.
![]()
Die Rechnung mit der Näherungszahl für die Wurzel ergibt dann das genaue Ergebnis der Näherungsrechung:
![]() .
.
![]()
Auch hier ergibt sich mit der Näherungszahl für die Wurzel ein genaues Ergebnis der Näherungsrechnung:
![]() .
.
![]()
Die Rechnung mit den Näherungszahlen ergibt:
![]() .
.
Die 3 Beispiele lassen sich wie folgt verallgemeinern:
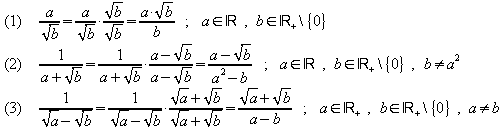
Nach Definition des Begriffes „Potenz“ ist![]() .
.
Andererseits gilt: ![]() .
.
Also ist ![]() .
.
In Verallgemeinerung des Beispiels ergibt sich:
also:
Übung:
Untersuchen Sie an Beispielen, ob die Aussage
Ö(a + b) = Öa + Öb
richtig ist. Versuchen Sie, eine allgemeine Begründung für Ihr Ergebnis zu geben.