3. Die Menge der reellen Zahlen

1) Intervall-Halbierungs-Verfahren

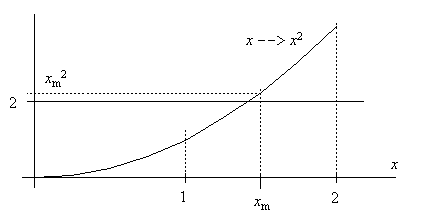
Erster Schritt:

Es wird ein Intervall [x_links ; x_rechts] gesucht, in dem die Lösung liegt.
 Ein geeignetes Intervall ist x_links = 1 und x_rechts = 2, denn: 1² < 2 < 2².

Zweiter Schritt:

Es wird der Mittelpunkt x_m des Intervalls berechnet:

also

.

Dritter Schritt:

Es wirdgebildet und mit 2 verglichen:

Daist, wird x_m als neue rechte Intervallgrenze gewählt:

Die gesuchte Lösung ist jetzt durch ein Intervall eingegrenzt, das nur noch halb so breit ist wie das Ausgangsintervall:

Wiederholung von Schritt 2:

Berechnung des Mittelpunktes x_m des halbierten Intervalls:

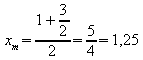
Wiederholung von Schritt 3:

Es wirdgebildet und mit 2 verglichen:

Daist, wird x_m als neue linke Intervallgrenze gewählt:

Die gesuchte Lösung ist jetzt durch ein Intervall eingegrenzt, das nur noch halb so breit ist wie das vorige Intervall:

Wiederholung von Schritt 2:

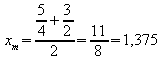
Wiederholung von Schritt 3:

Schritt 2 und Schritt 3 werden solange wiederholt, bis eine gewünschte Genauigkeit erreicht ist.

Mit dem folgenden JavaScript können Sie zu positiven Zahlen r die Wurzel mit dem Intervall-Halbierungs-Verfahren näherungsweise berechnen.
Wählen Sie z.B. r = 2; 3; 5; 8; ....
Experimentieren Sie mit verschiedenen Ausgangsnäherungen für x_links und x_rechts. (Beachten Sie bitte: bei Dezimalzahlen ist ein Dezimalpunkt, kein Komma einzugeben.)
Versuchen Sie, Ör möglichst genau anzunähern.
 

2) Heron-Verfahren

Ö2 ist die positive Lösung von x² = 2.

Geometrisch betrachtet sucht man also die Seitenlänge eines Quadrates, dessen Flächeninhalt 2 Einheiten beträgt.
 

Schritt 1: Ausgegangen wird von einem Rechteck mit dem Flächeninhalt A = 2 und Seitenlängen Durch Verlängern der einen Seite und Verkürzen der anderen Seite wird dieses Rechteck in ein flächengleiches Rechteck umgewandelt, das einem Quadrat „ähnlicher“ ist.
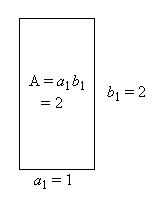Schritt 2: a) Ersetze b1 durch den Mittelwert von a1 und b1: . b) Bestimme a2 so, dass ist, also: Damit ist Ö2 genauer eingeschachtelt: .

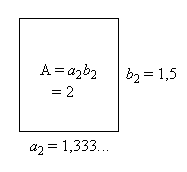Wiederholung von Schritt 2:

a) Ersetze b₂ durch den Mittelwert von a₂ und b₂:

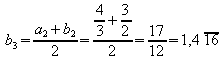
b) Bestimme a₃ so, dass ist, also:

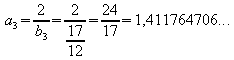
Damit ist Ö2 genauer eingeschachtelt: .
 

Diese Rechenschritte werden solange wiederholt, bis eine gewünschte Genauigkeit erreicht ist.

Auch hier haben Sie die Möglichkeit, mit einem JavaScript eigene Experimente zum Heron-Verfahren anzustellen.

Wählen Sie auch hier verschiedene Radikanden und unterschiedliche Ausgangsnäherungen. (Beachten Sie bitte: bei Dezimalzahlen ist ein Dezimalpunkt, kein Komma einzugeben.)
 

Intervallschachtelungen

Mengen, wie,,

nennt man (abgeschlossene) Intervalle. Häufig wird dafür kurz geschrieben:

.

Die Länge eines Intervalls [a ; b] wird durch | b – a | angegeben, da dieser Term den Abstand der Zahlen a und b auf der Zahlengeraden angibt.
 

Definition: Eine Intervallschachtelung ist eine Folge von abgeschlossenen Intervallen mit den Eigenschaften: 1)  2) Wenn n beliebig groß wird, geht die Länge der Intervalle gegen Null.

Das Intervall-Halbierungs-Verfahren, das oben zur Berechnung von Näherungszahlen für Ö2 benutzt wurde, liefert Intervall-Schachtelungen, wenn es auf Ör , r > 0 angewendet wird. Auch das Heron-Verfahren ergibt Intervall-Schachtelungen, wie hier jedoch nicht bewiesen werden soll.

Für den weiteren Aufbau des Zahlensystems ist der folgende Satz entscheidend.
 

Intervallschachtelungsaxiom: Zu jeder Intervallschachtelung gibt es eine eindeutig bestimmte Zahl x0, die dadurch gekennzeichnet ist, dass sie allen Intervallen der Schachtelung angehört.  x0 heißt innere Zahl der Intervallschachtelung.

Dieses Axiom bringt zum Ausdruck, dass jeder Stelle auf der Zahlengeraden eine Zahl zugeordnet wird.

Zu beachten ist: Jede Intervallschachtelung zieht sich auf genau eine Stelle der Zahlengeraden zusammen. Umgekehrt kann es aber zu einer Stelle verschiedene Intervallschachtelungen geben. Beispiele dafür sind schon die Intervallschachtelungen für Ö2, die am Anfang dieses Abschnitts ermittelt wurden:

Intervall-Halbierungs-Verfahren:

Heron-Verfahren:

Die innere Zahl einer Intervallschachtelung ist

• entweder eine rationale Zahl; ihre Dezimaldarstellung ist dann abbrechend oder periodisch;
• oder keine rationale Zahl; ihre Dezimaldarstellung muss dann nicht-abbrechend und nicht-periodisch sein.

 

Definition: Alle inneren Zahlen von Intervallschachtelungen bilden die Menge der reellen Zahlen.

Die Zahlen, deren Dezimaldarstellung nicht-periodisch und nicht-abbrechend ist, bilden die Menge der Irrationalzahlen I. Sie ist eine Teilmenge der reellen Zahlen:.

 Die Menge der rationalen Zahlen ist ebenfalls eine Teilmenge der reellen Zahlen:.

 Außerdem gilt:.

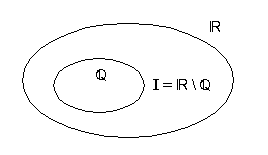
Es gibt also „mehr“ reelle Zahlen als rationale Zahlen. Tatsächlich ist die Menge der reellen Zahlen nicht mehr abzählbar. Schon das offene Intervallist nicht mehr abzählbar, wie Cantor mit folgender Überlegung zeigte.

Angenommen, es sei möglich, eine Liste der reellen Zahlen zwischen 0 und 1 aufzustellen. Dann kann man ihre Dezimaldarstellungen untereinander schreiben, und eine solche Liste könnte wie folgt aussehen:

1. Zahl: 0.5148309752971...

2. Zahl: 0,4354354354354...

3. Zahl: 0,1415926540308...

4. Zahl: 0,9819025736626...

5. Zahl: 0,6392347543742...

usw. ..................

Das Cantor'sche Verfahren besteht darin, eine reelle Zahl zwischen 0 und 1 anzugeben, die nicht in der Liste enthalten ist. Und das geht verblüffend einfach: Wählen Sie einfach eine Zahl,

• deren erste Nachkommastelle (Zehntel-Stelle) mit der ersten Nachkommastelle der ersten Zahl (im obigen Beispiel: 5) nicht übereinstimmt,
• deren zweite Nachkommastelle (Hundertstel-Stelle) mit der zweiten Nachkommastelle der zweiten Zahl (im obigen Beispiel: 3) nicht übereinstimmt,
• deren dritte Nachkommastelle (Tausendstel-Stelle) mit der dritten Nachkommastelle der drittenZahl (im obigen Beispiel: 1) nicht übereinstimmt, usw.

So eine Zahl ist von allen bereits in der Liste stehenden Zahlen verschieden. (Sie unterscheidet sich von der n-ten Zahl der Liste in der n-ten Nachkommastelle).

Für obiges Beispiel:

1. Zahl: 0,5148309752971...

2. Zahl: 0,4354354354354...

3. Zahl: 0,1415926540308...

4. Zahl: 0,9819025736626...

5. Zahl: 0,6392347543742...

 usw. ..................

Hinzugefügt wird nun eine Zahl, die sich von allen angegebenen Zahlen unterscheidet:

neue Zahl: 0,64204...............

Dieses Verfahren kann immer angewendet werden, ganz gleich, welche Liste von Zahlen zunächst hingeschrieben wurde.

Das Argument zeigt, dass so eine Liste nie alle reellen Zahlen zwischen 0 und 1 umfassen kann (und daher auch nicht die ganze Menge R). Womit bewiesen ist:
 

Die Mengeist überabzählbar.

Daraus ergibt sich weiter, dass auch die Menge der irrationalen Zahlen überabzählbar ist. Sie bildet den Löwenanteil in der Menge. Folgende Überlegung soll dies verdeutlichen.

Auf der Zahlengeraden sei der Einfachheit halber der Abstand zwischen zwei benachbarten ganzen Zahlen jeweils 1 cm. Die rationalen Zahlen sind abzählbar – sie können z.B. in der Liste

aufgezählt werden. Denken Sie sich nun die erste rationale Zahl mit einer Kreisscheibe von 1 cm Durchmesser abgedeckt. Die zweite rationale Zahl werde mit einer Kreisscheibe vom Durchmesser 0,1 cm, die dritte mit einer Kreisscheibe vom Durchmesser 0,01 cm abgedeckt usw. Mit diesem Verfahren werden alle rationalen Zahlen abgedeckt. Natürlich werden sich dabei die Kreisscheiben überlappen. Denkt man sich nun die ganzen Kreisscheiben so verschoben, dass sie sich nicht mehr überlappen, sondern aneinander stoßen. Die Länge aller nebeneinander liegenden Kreisscheiben ist dann

Die gesamten Kreisscheiben decken also auf der Zahlengeraden nur eine Strecke der Länge 10/9 cm ab...

Man kann natürlich für die erste Kreisscheibe auch einen Durchmesser von 0,1 cm wählen, für die zweite einen Durchmesser von 0,01 cm usw. Für die Länge aller nebeneinander gelegten Kreisscheiben erhält man dann:

Die rationalen Zahlen, mit denen man es in der Praxis so oft zu tun hat, und die in so vielen Rechenaufgaben vorkommen, bilden genau genommen nur eine verschwindende Minderheit. Man nennt sie auch „nicht-vollständig“, da sie nicht die ganze Zahlengerade „ausfüllen“, aber „dicht'“, da in jedem noch so kleinen Intervall rationale Zahlen liegen.