2. Teiler und Vielfache

Teiler

Jede Zahl n hat die trivialen Teiler 1 und n, denn: . Alle anderen Teiler von n nennt man echte Teiler von n.

Für Teiler gelten zwei einfache Sätze.

Satz 1: Wenn eine Zahl t Teiler einer Zahl a ist, so ist sie auch Teiler aller Vielfachen von a.

Dieser Satz soll zunächst an einem Beispiel dargestellt werden:

Diese Überlegung lässt sich allgemein, also ohne Bezug auf spezielle Beispielwerte, formulieren:

Satz 2: Wenn eine Zahl t Teiler einer Zahl a und Teiler einer Zahl b ist (a > b), dann ist t auch ein Teiler der Summe a + b und der Differenz a – b .

Beispiel:

Auch dieser Zusammenhang lässt sich allgemein zeigen:

Ersetzt man in dieser Überlegung „+“ durch „– “ so ergibt sich die Aussage über die Differenz.

Die Umkehrung des Satzes gilt nicht, wie das Beispiel 21 = 17 + 4 zeigt. 3 ist ein Teiler der Summe: 3^.7 = 21; aber 3 ist kein Teiler von 17 und kein Teiler von 4.

Primzahlen

Eine natürliche Zahl p, die außer den trivialen Teilern 1 und p (sich selbst) keine weiteren Teiler hat, heißt Primzahl. So ist z.B. 5 nur durch 1 und 5, 13 nur durch 1 und 13 teilbar; 5 und 13 sind also Primzahlen. Die Zahl 1 wird nicht zu den Primzahlen gerechnet, so dass die Primzahlfolge mit 2 beginnt: 2, 3, 5, 7, 11, 13, 17, 19, 23, ...

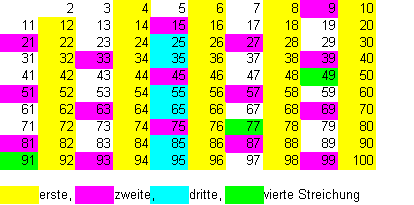
Der griechische Mathematiker Eratosthenes (etwa 200 v.Chr.) gab folgendes Verfahren an, um sämtliche Primzahlen in einem Abschnitt der natürlichen Zahlen zu finden („Sieb des Eratosthenes“). Man streicht aus dem Abschnitt nach der 2 jede durch 2 teilbare Zahl, dann nach der 3 jede durch 3 teilbare Zahl, dann nach der 5 jede durch 5 teilbare Zahl usw. Es bleiben gerade die Primzahlen des Abschnitts stehen. Beispiel: Bis zur 100 sind so nur 4 Streichungen nötig, die letzte davon für alle durch 7 teilbaren Zahlen. Das liegt daran, dass 7^.7 = 49 < 100, aber bereits 11^.11 = 121 > 100 ist; 11 ist ja die auf 7 folgende nicht gestrichene Zahl, also die nächste Primzahl.

Jede natürliche Zahl n (n > 1), die nicht Primzahl ist, kann als Produkt von Primzahlen (Primfaktoren) geschrieben werden. Dieses Produkt wird auch Primfaktorzerlegung von n genannt. Bei der Bestimmung einer Primfaktorzerlegung kann man probieren:

Es kann aber auch schematisch vorgegangen werden:

Ein anderes Beispiel:

Kann es noch andere Primfaktorzerlegungen dieser Zahl geben? Diese Frage beantwortet der
 

Satz: Die Zerlegung einer natürlichen Zahl in Primfaktoren ist eindeutig.

Zum Beweis wird zunächst angenommen, dass eine natürliche Zahl n zwei verschiedene Primfaktorzerlegungen besitzt:

Dann gilt

Nun ist p₁ ein Teiler der linken Seite, also muss p₁ auch ein Teiler der rechten Seite sein. Da rechts aber nur Primzahlen stehen, muss p₁ gleich einem der Faktoren rechts sein. Wegen der Kommutativität der Multiplikation kann man die Primfaktoren q_i (bei Bedarf) so umordnen, dass

ist. Es bleibt nach Division durch p₁ übrig:

Für p₂ kann dieselbe Überlegung wie für p₁ angestellt werden. Daraus ergibt sich:

Nach Division durch p₂ bleibt übrig:

So wird weiter verfahren, und man erhält nacheinander:

Nach den Divisionen durch bleibt übrig:

Dies ist nur möglich, wenn. Also muss schon r = s sein. Damit ist die Eindeutigkeit der Primfaktorzerlegung nachgewiesen.

Gemeinsame Teiler

Ist eine natürliche Zahl g sowohl Teiler einer natürlichen Zahl a als auch Teiler einer natürlichen Zahl b, so heißt g gemeinsamer Teiler von a und b.

Der größte gemeinsame Teiler wird mit ggT(a;b) bezeichnet.

Den ggT zweier Zahlen erhält man aus deren Primfaktorzerlegungen, wenn man die höchsten Potenzen aller Primfaktoren multipliziert, die in beiden Zerlegungen gemeinsam vorkommen.
 

1)	2)
3)	4)

Im letzten Beispiel sind die beiden Zahlen teilerfremd – d.h. es ist ggT = 1.

Bei 3 Zahlen (oder noch mehr) kann genauso vorgegangen werden:

Es ist auch möglich, schrittweise vorzugehen. Beispiel: Es soll zu drei Zahlen a, b, c der ggT bestimmt werden.

1. Bestimme den ggT von zwei der drei Zahlen, z. B. ggT(a;b).
2. Bestimme dann den ggT von ggT(a;b) und c, also: g = ggT(ggT(a;b);c)

Die so erhaltene Zahl g ist Teiler von ggT(a;b). Ein Teiler des ggT zweier Zahlen ist auch ein Teiler der beiden Zahlen, also ist g auch Teiler von a und Teiler von b. Außerdem ist g Teiler von c. Somit ist g der ggT von a, b, c.

Zusammengefasst:

Bei größeren Zahlen ist die Bestimmung der Primfaktorzerlegung mühsam. Man kann zur Bestimmung des ggT zweier Zahlen auch anders vorgehen. Dies soll zunächst an einem Beispiel erläutert werden.

Der ggT von a = 60 und b = 42
                    ist auch Teiler der Differenz c = 60 – 42 = 18

(siehe Satz 2 im Abschnitt „Teiler“). Er ist auch der ggT von a, b und c = a - b , denn es gilt:

Dann ist der ggT(a,b)
auch ggT von a₁ := b = 42 und b₁ := c = 18
                    und Teiler der Differenz c₁ = a₁ – b₁ = 42 – 18 = 24
und ggT von a₂ := c₁ = 24 und b₂ := b₁ = 18
                    und Teiler der Differenz c₃ = a₂ – b₂ = 24 – 18 = 6
und ggT von a₃ := b₂ = 18 und b₃ := c₃ = 6
                    und Teiler der Differenz c₄ = a₃ – b₃ = 18 – 6 = 12
und ggT von a₄ := c₄ = 12 und b₄ := b₃ = 6
                    und Teiler der Differenz c₅ = a₄ – b₄ = 12 – 6 = 6
und ggT von a₅ := b₄ = 6 und b₅ := c₅ = 6.
Damit ist also: ggT(60;42) = 6.

Schematisch lässt sich dieses Verfahren so beschreiben:

Das Verfahren lässt sich noch verkürzen:

60 – 18 = 42
42	– 18 = 24
	24	– 18 = 6
		18	– 6 = 12
			12	– 6 = 6
				6	– 6 = 0

Die fortlaufenden Subtraktionen können durch Division mit Rest ersetzt werden:

60 : 18 = 3 Rest 6
18 :   6 = 3 Rest 0

Damit ist der ggT gefunden: ggT(60;18) = 6.

Dieses Verfahren heißt Euklidischer Algorithmus (Euklid, um 300 v.Chr.). Ein weiteres Beispiel:

a = 16 b = 6

16 : 6 = 2 Rest 4
  6 : 4 = 1 Rest 2
  4 : 2 = 2 Rest 0
also: ggT(16;6) = 2.

Schematisch lautet der Euklidische Algorithmus:

Ein nicht ganz so einfaches Beispiel: a = 53667, b = 25527;

53667 : 25527 = 2 + 2613
25527 :   2613 = 9 + 2010
  2613 :   2010 = 1 + 603
  2010 :     603 = 3 + 201
    603 :     201 = 3 + 0

also: ggT(53667; 25527) = 201.

Vielfache und gemeinsame Vielfache

Eine Zahl v heißt Vielfaches einer Zahl a, wenn es eine natürliche Zahl n gibt mit .

Beispiel: 584 ist Vielfaches von 73, denn es ist 584 = 8^.73.

Der Zusammenhang lässt sich auch so ausdrücken: v ist Vielfaches von a, wenn a ein Teiler von v ist: .

Ist eine Zahl v sowohl Vielfaches einer Zahl a als auch Vielfaches einer Zahl b, so heißt v gemeinsames Vielfaches von a und b. Das kleinste gemeinsame Vielfache wird mit kgV bezeichnet.

Das kgV zweier Zahlen erhält man aus deren Primfaktorzerlegungen, wenn man die höchsten Potenzen aller vorkommenden Primfaktoren multipliziert.

Bei mehr als zwei Zahlen wird genauso vorgegangen:

Bei größeren Zahlen ist dieses Verfahren wegen der Primfaktorzerlegung ungünstig. Man kann dann folgenden Zusammenhang ausnutzen:

Der ggT kann mit dem Euklidischen Algorithmus ermittelt werden, so dass keine Primfaktorzerlegung nötig ist.

Übung:

Berechnen Sie für die folgenden Zahlen jeweils den ggT durch Primfaktorzerlegung und durch Euklidischen Algorithmus und das kgV durch Primfaktorzerlegung und durch Anwenden der Beziehung zwischen kgV und ggT.

a) a = 80, b = 12

b) a = 96, b = 28

c) a = 147, b = 56

Die folgenden JavaScript-Programme können zur Kontrolle verwendet werden.