1.
![]() = { W1, W2, ...,
W6, Z1, Z2, ..., Z6 }
= { W1, W2, ...,
W6, Z1, Z2, ..., Z6 }
2.
![]() = { 2, 3, 4,
..., 12 }
= { 2, 3, 4,
..., 12 }
3.
![]() = { (rr), (rs),
(rw), (sr), (sw), (wr), (ws), (ww) }
= { (rr), (rs),
(rw), (sr), (sw), (wr), (ws), (ww) }
4.
![]() = { bbb, bbg,
bbw, bgg, bgw, bww, ggg, ggw, gww, www }
= { bbb, bbg,
bbw, bgg, bgw, bww, ggg, ggw, gww, www }
5.
![]() = { (1;2;3),
(1;3;2), (2;1;3), (2;3;1), (3;1;2), (3;2;1) } ;
= { (1;2;3),
(1;3;2), (2;1;3), (2;3;1), (3;1;2), (3;2;1) } ; ![]()
6.
![]() = { (A;A),
(A;B;A), (A;B;B), (B;B), (B;A;B), (B;AA) }
= { (A;A),
(A;B;A), (A;B;B), (B;B), (B;A;B), (B;AA) }
7.
![]() = { (J;J;J),
(J;J;M), (J;M;J), (J;M;M), (M;J;J), (M;J;M), (M:M;J),
(M;M;M) }
= { (J;J;J),
(J;J;M), (J;M;J), (J;M;M), (M;J;J), (M;J;M), (M:M;J),
(M;M;M) }
8.
a) ![]() = { www , wws,
wss }
= { www , wws,
wss }
b) ![]() = { (www),
(wws), (wsw), (wss), (sww), (sws), (ssw) }
= { (www),
(wws), (wsw), (wss), (sww), (sws), (ssw) }
c) ![]() = { (www),
(wws), (wsw), (wss), (sww), (sws), (ssw), (sss) }
= { (www),
(wws), (wsw), (wss), (sww), (sws), (ssw), (sss) }
9.
![]()
1.
![]() = { 11, 12, 13,
14, 15, 16, 22, 23, 24, 25, 26, 33, 34, 35, 36, 44, 45, 46,
55, 56, 66 }
= { 11, 12, 13,
14, 15, 16, 22, 23, 24, 25, 26, 33, 34, 35, 36, 44, 45, 46,
55, 56, 66 }
E1 = { 11, 12, 13, 22 }
E2 = { 16, 25, 26, 34, 35, 36, 44, 45, 46, 55, 56, 66 }
2.
![]() = { (NNN),
(TNN), (NTN), (NNT), (TTN), (TNT), (NTT) }
= { (NNN),
(TNN), (NTN), (NNT), (TTN), (TNT), (NTT) }
E0 = { (NNN) }
E1 = { (TNN), (NTN), (NNT) }
E2 = { (TTN), (TNT), (NTT) }
3. a) ![]() = { (rr), (rb), (rg), (br), (bg), (gr), (gb), (gg) }
= { (rr), (rb), (rg), (br), (bg), (gr), (gb), (gg) }
E0 = { (bg), (gb), (gg) }
E1 = { (rb), (rg), (br), (gr) }
b) ![]() = { (rr), (rb), (rg), (bb), (br), (bg), (gr), (gb), (gg) }
= { (rr), (rb), (rg), (bb), (br), (bg), (gr), (gb), (gg) }
E0 = { (bb), (bg), (gb), (gg) }
E1 = { (rb), (rg), (br), (gr) }
4. ![]() = { 11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42,
43, 44 }
= { 11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42,
43, 44 }
A = { 11, 13, 21, 23, 31, 33, 41, 43 }
B = { 13, 22, 31, 44 }
C = { 11, 12, 13, 14, 21, 22, 23, 24 }
D = ( 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44 )
5. ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]()
6. a) ![]() = { (111), (110), (101), (011), (100), (010), (001), (000) }
= { (111), (110), (101), (011), (100), (010), (001), (000) }
b) ![]() ;
; ![]() ;
; ![]()
7. a) ![]() = { 11, 12, 13, 14,
15, 16, 22, 23, ..., 26, ..., 66 }
= { 11, 12, 13, 14,
15, 16, 22, 23, ..., 26, ..., 66 }
b) ![]()
1. 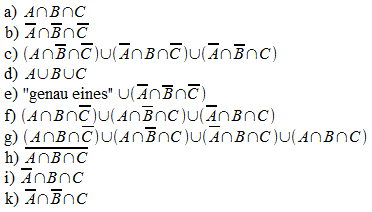
2. -
3. a) ![]() = { (0000), (1000), (0100), (0010), (0001), (1100), (1010),
(1001), (0110), (0101), (0011), (1110), (1101), (1011),
(0111), (1111) }
= { (0000), (1000), (0100), (0010), (0001), (1100), (1010),
(1001), (0110), (0101), (0011), (1110), (1101), (1011),
(0111), (1111) }
b) 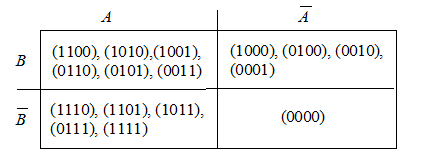
c) 
4. a) ![]() = { (ABC), (ACB), (BAC), (BCA), (CAB), (CBA) }
= { (ABC), (ACB), (BAC), (BCA), (CAB), (CBA) }
b) 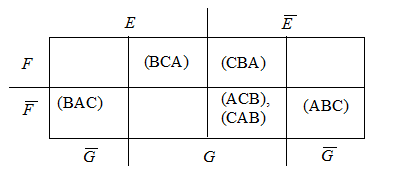
c) 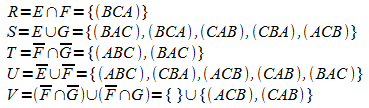
1. a) h1000(ZZ) = 0,246 ; h1000(ZW) = 0,245 ; h1000(WZ) = 0,232 ; h1000(WW) = 0,268
b) h1000(A) = 0,468 ; h1000(ZZ) = 0,514 ; h1000(C) = 0,754 ; h1000(D) = 0,732
2. a) h200(A) = 0,04 ; h200(B) = 0,10 ; h200(C) = 0,08
b) ![]()
c) 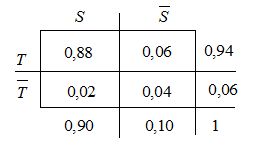
d) ![]()
3. a) 
b) 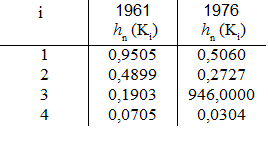
4. a) 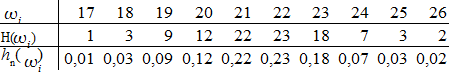
b) hn(A) = 0,63 ; hn(B) = 0,13
1. a) ![]()
b) ![]()
2. a) ![]()
b) ![]()
3. ![]()
4 a) ![]()
b) 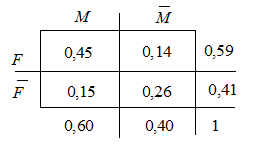
1. ![]() = { (1,1), (1,2), ..., (1,6), (2,1), (2,2), ..., (2,6), ...,
(6,1), (6,2), ..., (6,6) } ;
= { (1,1), (1,2), ..., (1,6), (2,1), (2,2), ..., (2,6), ...,
(6,1), (6,2), ..., (6,6) } ;
![]()
E = { (2,6), (3,5),
(4,4), (5,3), (6,2) } ;
![]()
![]()
2. a) gleichzeitiges Ziehen von 2 Kugeln entspricht dem Ziehen von 2 Kugeln nacheinander ohne Berücksichtigung der Reihenfolge
![]() = { s1s2, s1s3, s1w1, s1w2,
= { s1s2, s1s3, s1w1, s1w2,
s2s3, s2w1, s2w2,
s3w1, s3w2,
w1w2 } ;
![]()
E = { s1w1, s1w2,
s2w1, s2w2, s3w1, s3w2 } ;
![]()
![]()
b) ![]() = {
(s1,s1), (s1,s2), (s1,s3),( s1,w1), (s1,w2),
= {
(s1,s1), (s1,s2), (s1,s3),( s1,w1), (s1,w2),
(s2,s1), (s2,s2), (s2,s3), (s2,w1), (s2,w2),
(s3,s1), ..., (s3,w2),
(w1,s1), ..., (w1,w2),
(w2,s1), ..., (w2,w2) } ;
![]()
E = { (s1,s1),
(s1,s2), (s1,s3), (s2,s1), (s2,s2), (s2,s3), (s3,s1),
(s3,s2), (s3,s3),
(w1,w1), (w1,w2), (w2,w1), (w2,w2) } ;
![]()
![]()
![]()
VoW = 32 760
1. VmW = 28 = 256
2. VmW = 324 = 1 048 576
1. 300
2. ![]()
3. ![]()
4. ![]()
5. 12 620 256
1. KmW = 21
2. KmW = 20
1. a) KoW = 20
b) KoW = 4
c) ![]()
2. a) PoW = 5
b) PoW = 4
c) 8 * 3! = 48
3. a) 3 * 360 = 1080
b) 3 * 64 = 3888
4. a) VoW = 360
b) VoW = 46 267 920
5. KoW * KoW = 792 * 35 = 27720
6. a) PoW = 720
b) VoW = 120
c) an der 361. Stelle
7. 2 520
8. a) 1024 ; gleichwahrscheinlich
b) 11 ; nicht gleichwahrscheinlich
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. a) ![]()
b) ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
1.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
Die Wahrscheinlichkeit für Diabeteserkrankung ist bei männlichen Patienten größer als bei weiblichen.
2.
a) 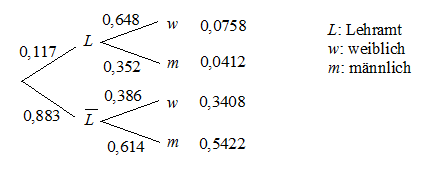
b)
|
|
L |
nicht L |
|
|
w |
7,58% |
34,08% |
41,66% |
|
m |
4,12% |
54,22% |
58,34% |
|
|
11,7% |
88,3% |
100% |
1.
a) (1) ![]()
(2) 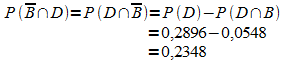
(3) 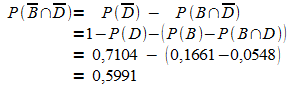
b)
|
|
B |
nicht B |
|
|
D |
0,05% |
0,23% |
0,2896 |
|
nicht D |
0,11% |
0,60% |
0,7104 |
|
|
0,1661 |
0,8339 |
1 |
|
zugehöriges Baumdiagramm:
|
umgekehrtes Baumdiagramm:
|
2. a)
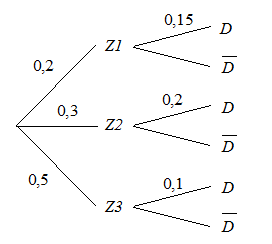
b) 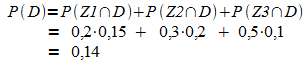
c) 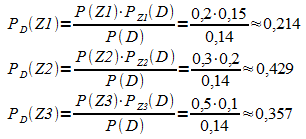
1. a)
|
|
V |
nicht V |
|
|
B |
12/125 |
63/125 |
3/5 |
|
nicht B |
8/125 |
42/125 |
2/5 |
|
|
4/25 |
21/25 |
1 |
b) Alle Ereignisse sind stochastisch unabhängig.
2. A und B sind stochastisch unabhängig.
3.
|
|
A |
nicht A |
|
|
B |
0,03 |
0,07 |
0,1 |
|
nicht B |
0,27 |
0,63 |
0,9 |
|
|
0,3 |
0,7 |
1 |
4.
a) ![]()
b) ![]()
1. a) -
b) (a) 2/9 (b) 2/9 (c) 4/9 (d) 1/9 (e) 4/9
2. a) 4,41% b) 4,41% c) 8,82% d) 1,89% e) 2,7% f) 26,46%
3. a) 1,93% b) 11,57%
4. a) 34,87% b) 65,13% c) 0,43%
5. 96,41%
1. a) 29,1% b) 77,52%
2. 40,46%
3. 4,53%
4. 3,55%
5. a) 21,5% b) 0,01% c) 0,6% d) 99,39% e) 16,72%
1. 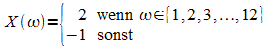
2. 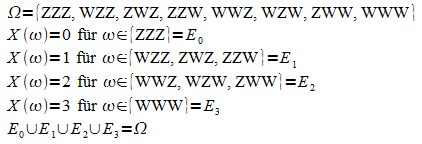
3.
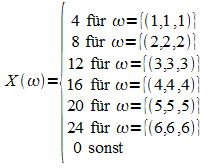
1. a) P(X = 5) = 6/37 ; P(X = -1) = 31/37
b) -
2. a) 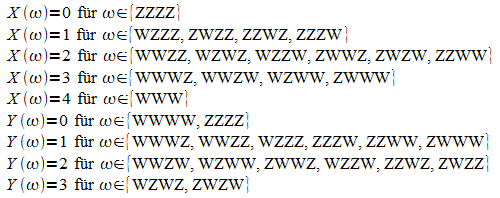
b) 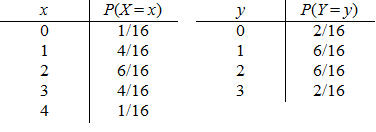
3. a) ![]()
b) 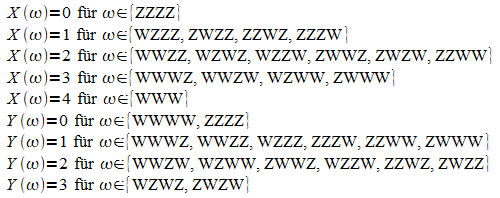
c) 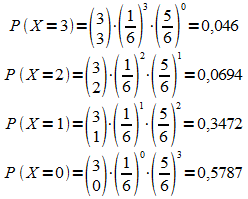
1. 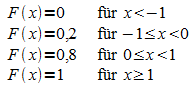
2. a) 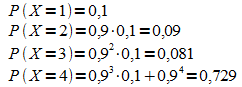
b) 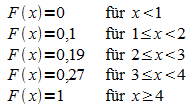
3. a) 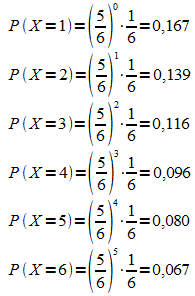
b) 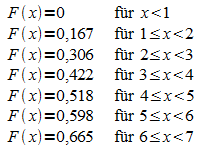
c) ![]()
d) ![]()
Ereignis: „Man kommt mit höchstens 6 Würfen ins Spiel.“
e) ![]()
1.
|
Beispiel |
E(X) |
|
1 |
1/3 |
|
2 |
1,2 |
|
3 |
7 |
|
4 |
1,01 |
|
5 |
1 |
2. 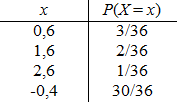
E(X) = -0,122
Im Durchschnitt verliert ein Spieler 12,2 Cent pro Spiel. Für den Veranstalter bedeutet dies den durchschnittlichen Gewinn von 12,2 Cent je Mitspieler.
3. a) 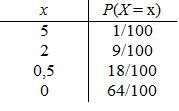
E(X) = 0,32
b) Bei einem Einsatz von 0,50 Euro macht der Automatenbesitzer Gewinn von 0,50 - 0,32 = 0,18 Euro.
1.
|
Beispiel |
Var(X) |
|
|
1 |
3,556 |
1,886 |
|
2 |
0,36 |
0,6 |
|
3 |
5,833 |
2,415 |
|
4 |
0,55 |
0,742 |
|
5 |
0,68 |
0,825 |
2. a) 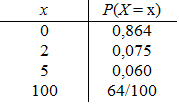
E(X) = 0,55
mittlerer Gewinn = Einsatz - E(X) = 0,45 Euro
b) ![]()
1. a) n = 20 ; p = 0,25
b) ![]()
c) ![]()
d) ![]()
2.
|
|
p |
E(X) |
Var(X) |
|
|
Würfel |
1/6 |
10,67 |
8,89 |
2,98 |
|
Tetraeder |
1/4 |
16 |
12 |
3,46 |
|
Münze |
1/2 |
32 |
16 |
4 |
|
Losziehung |
0,65 |
41,6 |
14,56 |
3,82 |
Der Erwartungswert wächst an. Varianz und Standardabweichung scheinen bei p = 1/2 maximal zu sein.
3.
|
|
1 |
2 |
3 |
|
n |
10 |
15 |
20 |
|
p |
0,7 |
0,7 |
0,7 |
|
E(X) |
7 |
10,5 |
14 |
|
Var(X) |
2,1 |
3,15 |
4,2 |
|
|
1,449 |
1,775 |
2,049 |
|
Treffer T |
8 |
12 |
16 |
|
|
1 |
1,5 |
2 |
|
|
0,690 |
0,845 |
0,976 |
An Stand 3 ergibt sich relativ gesehen das beste Ergebnis.