6.3 Bernoulli-Formel und Binomialverteilung

1. Ein Glücksrad trägt unterschiedlich große Felder. Der Mittelpunktswinkel von G sei 54°.

Als Treffer wird gewertet, wenn das Glücksrad nach dem Drehen auf dem Feld G stehen bleibt. Es ist also

Es wird n = 10 mal gedreht. Wie groß ist die Wahrscheinlichkeit, dass genau 4 Treffer erzielt werden (Ereignis E)?

Die 4 Treffer können in den Versuchen 1 bis 4 erzielt werden: E₁ = TTTTNNNNNN. Da die Versuche voneinander unabhängig sind, beträgt die Wahrscheinlichkeit dafür

Die 4 Treffer und die 6 Nieten können aber auch in anderer Reihenfolge auftreten, z.B.

NNTNTTNNTN,

TNNNTNTNNT,

usw.

Zu fragen ist also: Wie viele Möglichkeiten gibt es, dass von 10 Versuchen genau 4 das Ergebnis T haben. Anders formuliert: Auf wie viele Weisen kann man aus der Menge der 10 Plätze, auf denen die Versuchsausgänge notiert werden, 4 Plätze herauszugreifen? Dies ist auf

Arten möglich.

Für die gesuchte Wahrscheinlichkeit ergibt sich also:

2. Die Überlegungen zum Beispiel können leicht verallgmeinert werden. Bei einem Bernoulli- Experiment mit der Trefferwahrscheinlichkeit p und der Nietenwahrscheinlichkeit q = 1 – p ist die Wahrscheinlichkeit für genau k Treffer und n – k Nieten in einer Bernoulli-Kette der Länge n gegeben durch die Bernoulli-Formel

3. Die Trefferanzahl in einer Bernoulli-Kette der Länge n werde mit X bezeichnet: X = 0, 1, 2, ..., n. Die Wahrscheinlichkeit für k Treffer ist nach der Bernoulli-Formel

Jeder Trefferanzahl ist ihre Wahrscheinlichkeit zugeordnet. Eine solche Zuordnung bezeichnet man allgemein als eine Wahrscheinlichkeitsverteilung. Die vorliegende Wahrscheinlichkeitsverteilung

heißt Binomialverteilung.

Beispiel:

Das Beispiel des Tetraeder-Wurfs aus dem vorigen Abschnitt (Bernoulli-Kette) führt auf die Binomialverteilung. In der folgenden Tabelle sind die Wahrscheinlichkeiten für k Treffer zusammengestellt.

k	B(5; 0,25; k)
0
1
2
3
4
5

Die Summe der Wahrscheinlichkeiten B(5; 0,25; k) ergibt – wie zu erwarten war – 1.

Zur graphischen Darstellung von Wahrscheinlichkeitsverteilungen werden oft Histogramme verwendet. Wenn die Säulenbreite 1 gewählt wird, ergibt sich folgendes Bild für die Wahrscheinlichkeitsverteilung B(5; 0,25).

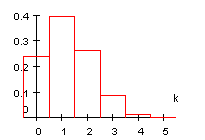
4. Die Berechnung der Werte B(n ; p ; k) kann rekursiv erfolgen:

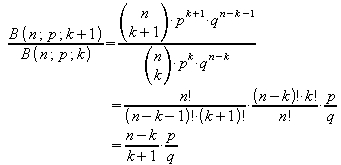
also:

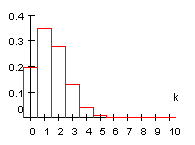
Unter Verwendung dieser Rekursionsformel ergeben sich für die Binomialverteilung B(10 ; 0,15 ) des Glücksrad-Beispiels folgende Werte:

k	B(10 ; 0,15 ; k)
0	0,19687
1	0,34743
2	0,27590
3	0,12983
4	0,04010
5	0,00849
6	0,00125
7	0,00013
8	0,00001
9
10

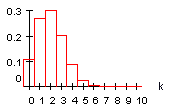
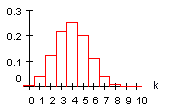
5. Die folgenden Histogramme zeigen Eigenschaften der Binomialverteilung.

a) festes n:

B(10 ; 0,2 ; k)
B(10 ; 0,4 ; k)
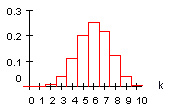
B(10 ; 0,6 ; k)
B(10 ; 0,8 ; k)

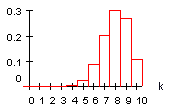1) Das Maximum (Stelle mit der größten Wahrscheinlichkeit) wandert bei festem n mit wachsendem Parameter p immer weiter nach rechts.

2) Von p = 0,1 bis p = 0,5 wird die Verteilung bei festem n breiter und niedriger, von 0, 5 bis 0,9 wieder schmaler und höher.

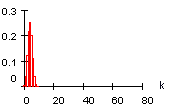
b) festes p:

B(10 ; 0,4 ; k)
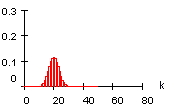
B(50 ; 0,4 ; k)
B(150 ; 0,4 ; k)

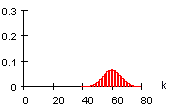3) Das Maximum wandert bei festem p mit wachsender Zahl n immer weiter nach rechts.

4) Die Verteilung wird bei festem p mit wachsender Zahl n breiter und niedriger.

6. In dem Glücksrad-Beispiel ist die Wahrscheinlichkeit, genau 4 Treffer zu erzielen

Die Ereignisse „Trefferzahl gleich i“, kurz X = i, sind unvereinbar, daher gilt für die Wahrscheinlichkeit, höchstens 4 Treffer zu erzielen

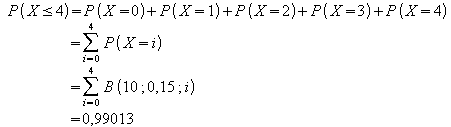
Die Wahrscheinlichkeit, mindestens 3 und höchstens 5 Treffer zu erzielen, ist

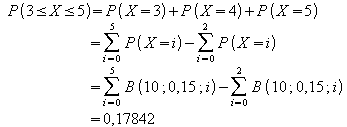
Die Summe der Wahrscheinlichkeiten in einem bestimmten Treffer-Intervall ist also von besonderer Bedeutung. Man definiert daher:

Definition: Die Funktionheißt kumulative Verteilungsfunktion der Binomialverteilung B(n ; p).

Beispiel: F(10 ; 0,15)

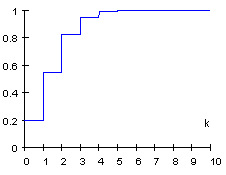
Mit den beiden folgenden JavaScript-Programmen können die Binomialverteilung und die kumulative Verteilungsfunktion zu beliebigem n und p berechnet werden. Für p ist auch die Eingabe von Brüchen zulässig, z.B. 1/6.

Binomialverteilung

Kumulative Verteilungsfunktion

Übungen

1. Bei einer als 2. Wahl angebotenen Sorte elektronischer Bauelemente ist 1/6 Ausschuss. Mit welcher Wahrscheinlichkeit enthalten 10 zufällig der Massenproduktion entnommene Bauelemente
a) genau zwei Fehlstücke,
b) bis zu zwei Fehlstücke?

2. Die Ausschusswahrscheinlichkeit eines mit einer bestimmten Maschine hergestellten Massenartikels sei erfahrungsgemäß 1%. Die Gegenstände werden in Packungen zu je 200 Stück versandt. Wie groß ist die Wahrscheinlichkeit, dass sich in einer Packung höchstens ein Ausschuss-Stück befindet?

3. Bei einer Prüfung wird ein „multiple-choice-Test“ mit Fragen angewendet. Es werden 5 Fragen gestellt. Zu jeder der Fragen sind in zufälliger Anordnung eine richtige und zwei falsche Antworten gegeben. Die Prüfung gilt als bestanden, wenn bei mindestens 4 Fragen die richtige Antwort angekreuzt ist. Ein unvorbereiteter Prüfling wählt seine Antworten rein zufällig aus. Mit welcher Wahrscheinlichkeit besteht er die Prüfung?

4. Wie groß ist die Wahrscheinlichkeit, beim 5-maligen Würfeln mehr als 2 „Sechsen“ zu erzielen?

5. Bei der Sortierung von Flaschen im Glasmüll sind 40% noch brauchbar. Es werden 10 Flaschen ausgewählt. Mit welcher Wahrscheinlichkeit
a) sind genau 3 Flaschen brauchbar?
b) sind alle 10 Flaschen brauchbar?
c) ist keine Flasche brauchbar?
d) ist mindestens 1 Flasche brauchbar?
e) sind höchstens 2 Flaschen brauchbar?