4.2 Satz von Bayes

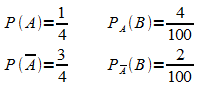
1. Beispiel 1: Eine Maschine M1 stellt Bauteile mit einem Ausschussanteil von 4% her. Eine zweite Maschine M2 produziert täglich dreimal soviele Bauteile wie M1, der Ausschussanteil beträgt dabei 2%.

Der Gesamtproduktion wird ein Bauteil zufällig entnommen, das sich als Ausschussteil erweist. Mit welcher Wahrscheinlichkeit stammt das Bauteil von der Maschine M1?

Für die Ereignisse

A: „Bauteil stammt von M1“,
B: „Bauteil ist Ausschuss“

sind der Beschreibung folgende Wahrscheinlichkeiten zu entnehmen:

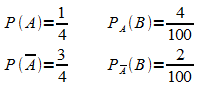
Diese können unmittelbar in das Baumdiagramm eingetragen werden. Durch Anwenden der 1. und der 2. Pfadregel ergeben sich dann die Pfadwahrscheinlichkeiten sowie :

Gesucht ist aber die Wahrscheinlichkeit , die im Baumdiagramm nicht erscheint. Für diese bedingte Wahrscheinlichkeit gilt:

.

Die benötigten Wahrscheinlichkeiten können mit dem Baumdiagramm bestimmt werden:

.

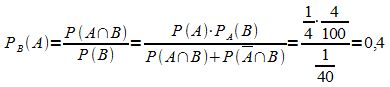2. Dieser Zusammenhang ist ein Beispiel für den Satz von Bayes (auch als Bayes'sche Regel bezeichnet):

Sei A ein interessierendes Ereignis, und B eine Bedingung, unter der das Ereignis eintritt.
Dann gilt: Die Wahrscheinlichkeit PB(A) für A unter der Bedingung B berechnet sich aus der Wahrscheinlichkeit PA(B) für B unter der Bedingung A wie folgt:

Dies folgt unmittelbar aus der Defintion der bedingten Wahrscheinlichkeit:

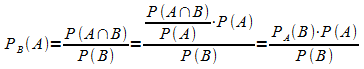
3. Vertauscht man bei einem Baumdiagramm die Reihenfolge der betrachteten Ereignisse, so erhält man das umgekehrte Baumdiagramm. Die Umkehrung des Baumdiagramms ist die Verallgemeinerung des Beispiels.

Baumdiagramm:

umgekehrtes Baumdiagramm:

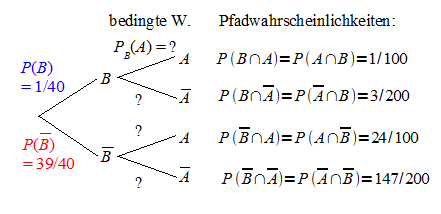
Die Pfadwahrscheinlichkeiten stimmen in beiden Baumdiagrammen bis auf die Reihenfolge überein. Die noch fehlenden bedingten Wahrscheinlichkeiten sind wie folgt mit den Daten des ursprünglichen Baumdiagramms zu ermitteln:

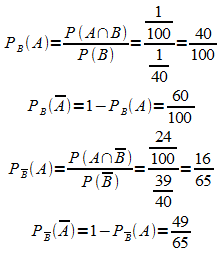
4. Beispiel 2: In einem Wahlkreis sind 30% der Wahlberechtigten über 70 Jahre alt; davon haben 40% die M-Partei gewählt. Unter den jüngeren Wahlberechtigten (bis 70 Jahre) beträgt der Anteil der M-Partei-Wähler 50%. Wieviel Prozent der M-Partei-Wähler sind höchstens 70 Jahre alt?

Bezeichnungen:

: M-Partei-Wähler : nicht-M-Partei-Wähler
: "jung" - bis 70 Jahre : "alt" - über 70 Jahre

Dem Text sind folgende Prozentangaben zu entnehmen, die als Wahrscheinlichkeiten interpretiert werden:

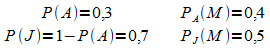
Gesucht ist die Wahrscheinlichkeit , die mit der Bayes'schen Regel berechnet werden kann:

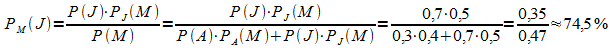
Zur Vertiefung sollen hier noch das Baumdiagramm und die 4-Felder-Tafel angegeben werden:

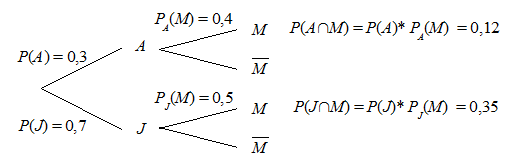
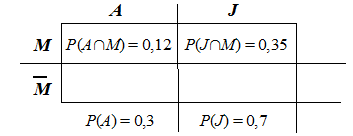
Die gesuchte Wahrscheinlichkeit ergibt sich damit zu

5. Beispiel 3: Gegeben sind drei Urnen mit folgenden Inhalten:

U1: 5 weiße und 3 schwarze Kugeln;
U2: 4 weiße und 6 schwarze Kugeln;
U3: 3 weiße Kugeln.

Eine der Urnen wird zufällig ausgewählt und dieser Urne wird eine Kugel entnommen. Es ist eine weiße Kugel. Wie groß ist die Wahrscheinlichkeit, dass die Kugel aus U1 entnommen wurde?

Bezeichnungen: A: Kugel aus U1
B: Kugel aus U2
C: Kugel aus U3
D: Kugel ist weiß

Der Beschreibung sind folgende Wahrscheinlichkeiten zu entnehmen:

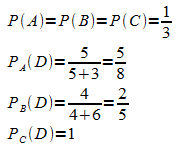
Gesucht ist .

Mit der 2. Pfadregel ergibt sich die (totale) Wahrscheinlichkeit, eine weiße Kugel zu ziehen:

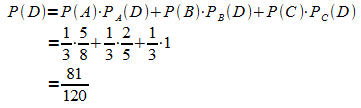
Die gesuchte Wahrscheinlichkeit ergibt sich mit dem Satz von Bayes:

Übungen

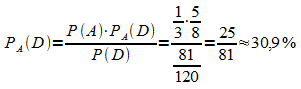
1. Den Statistiken des Kraftfahrt-Bundesamtes (http://www.kba.de) sind folgende Informationen zu entnehmen: Am 1.Januar 2013 waren in Deutschland insgesamt 43 431 124 PKW zugelassen. Davon waren 7 214 493 im Bundesland Bayern zugelassen (B). Einen Dieselmotor (D) hatten
12 578 950 Fahrzeuge, davon waren 2 378 145 in Bayern zugelassen.

a) Ein Fahrzeug werde zufällig ausgesucht. Berechnen Sie die folgenden Wahrscheinlichkeiten:

(1) das Fahrzeug ist in Bayern zugelassen;

(2) es ist ein Fahrzeug mit Dieselmotor, das in einem anderen Bundesland als Bayern zugelassen wurde;

(3) es ist ein in einem anderen Bundesland als Bayern zugelassenes Fahrzeug mit Benzinmotor.

b) Stellen Sie die Wahrscheinlichkeiten in einer 4-Felder-Tafel zusammen.
Geben Sie auch das zugehörige Baumdiagramm und das umgekehrte Baumdiagramm an.

2. Ein Hersteller von Waschmaschinen lässt bei einem bestimmten Maschinentyp Motoren von drei verschiedenen Zulieferfirmen einbauen. Nach einem Jahr nach Verkauf der Maschinen sind einige Motoren defekt.

a) Stellen Sie die Daten in einem Baumdiagramm zusammen.

b) Berechnen Sie die Wahrscheinlichkeit dafür, dass eine nach einem Jahr zufällig ausgewählte Maschine einen defekten Motor enthält.

c) Berechnen Sie die bedingten Wahrscheinlichkeiten dafür, dass einer der defekten Motoren in b) vom Zulieferer Z1 bzw. Z2 bzw. Z3 stammt.