3.5 Zusammenfassung und Übungen

3.5.1 Zusammenfassung

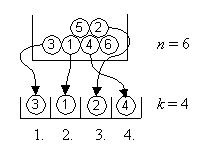
	ohne Wiederholung	mit Wiederholung
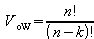
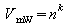
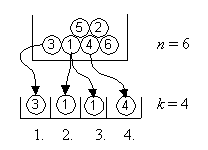
mit Anordnung (Variation bzw. Permutation)	Urnenmodell: nacheinander ziehen ohne Zurücklegen mit Berücksichtigung der Reihenfolge	Urnenmodell: nacheinander ziehen mit Zurücklegen mit Berücksichtigung der Reihenfolge
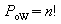
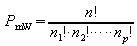
	Spezialfall: es werden alle Elemente genau einmal benutzt (n = k)	Spezialfall: es werden alle Elemente mindestens einmal benutzt mit n > p und n1 + n2 + ... + np = n
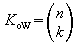
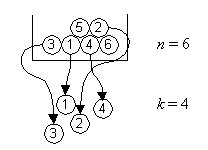
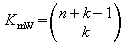
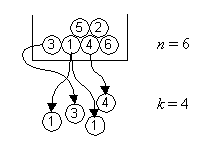
ohne Anordnung (Kombination)	Urnenmodell: nacheinander ziehen ohne Zurücklegen ohne Berücksichtigung der Reihenfolge	Urnenmodell: nacheinander ziehen mit Zurücklegen ohne Berücksichtigung der Reihenfolge

Beim Bearbeiten von Aufgaben aus der Kombinatorik sollte Folgendes beachtet werden:

• Machen Sie sich klar, wie die Ergebnisse einer Auswahl oder einer Verteilung aussehen.
• Kommt es auf eine Anordnung bzw. Reihenfolge der Zahlen oder Elemente an (werden also Tupel gebildet), so handelt es sich um eine Variation (bzw. Permutation).
• Kommt es nicht auf die Anordnung an (untersucht man also nur Mengen), dann liegt eine Kombination vor.
• Prüfen Sie, ob das Problem aus mehreren k-Auswahlen zusammengesetzt ist, so dass verschiedene Formeln mit jeweils unterschiedlichen Werten für n und k zu kombinieren sind (vgl. Zählprinzip).

3.5.2 Beispiele

1. Auf einer Mitgliederversammlung des Vereins „Freunde des andalusischen Zwergteddyhamsters“, der aus 11 Mitgliedern besteht, soll ein Wahlausschuss, bestehend aus 4 Mitgliedern gebildet werden. Wie viele Möglichkeiten gibt es, einen Wahlausschuss zusammenzustellen?

Eine Zusammenstellung des Wahlausschusses ist eine 4-Teilmenge aus einer 11-Menge.

Hier ist keine Reihen- oder Rangfolge vorgesehen. Außerdem kann natürlich jede Person nur einmal in dem Ausschuss vertreten sein. Es handelt sich also um eine 4-Kombination ohne Wiederholung aus 11 Personen: n = 11, k = 4.

Die Anzahl der verschiedenen Zusammensetzungen des Ausschusses ergibt sich also nach dem Lotto-Prinzip „4 aus 11“:

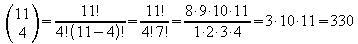2. Eine Teppich-Import-Firma beschäftigt 15 Mitarbeiter, der Firmenparkplatz hat aber nur 6 Plätze. Wie viele Belegungen des Parkplatzes sind möglich, wenn immer alle Mitarbeiter mit dem Auto zur Arbeit kommen und immer alle Plätze besetzt werden?

Eine Belegung ist ein 6-Tupel, dessen Stellen mit den Mitarbeitern 1 bis 15 besetzt werden.

Aus der Menge der 15 Mitarbeiter werden 6 ausgewählt. Es kommt aber auf die Anordnung an, wie die 6 auf die Parkplätze verteilt werden. Jede volle Belegung des Parkplatzes stellt daher eine 6-Variation ohne Wiederholung aus einer Menge von 15 Mitarbeitern dar. Es gibt also

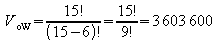
Belegungsmöglichkeiten.

3. a) Ein Würfel wird fünfmal geworfen. Wie viele Wurfergebnisse kann es geben?

Ein Wurfergebnis ist ein 5-Tupel, dessen Stellen mit den Ziffern 1 bis 6 besetzt werden.

Hier ist eine Anordnung der einzelnen Wurfergebnisse gegeben (erster Wurf, zweiter Wurf, ...). Bei jedem Wurf kann eine Augenzahl zwischen 1 und 6 auftreten. Es liegt also eine 5-Variation mit Wiederholung aus der Menge {1, 2, 3, 4, 5, 6} vor. Es ist n = 6 und k = 5, also gibt es

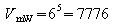
verschieden Wurfergebnisse.

b) 5 Würfel werden gleichzeitig geworfen. Wie viele Wurfergebnisse gibt es?

Ein Wurfergebnis ist eine 5-Menge, deren Elemente aus Elementen der 6-Menge {1, 2, 3, 4, 5, 6}bestehen (Wiederholungen möglich).
Das gleichzeitige Werfen bedeutet, dass keine Reihenfolge zu berücksichtigen ist. Jeder Würfel kann eine Augenzahl zwischen 1 und 6 aufweisen. Jeder Wurf ist daher eine 5-Kombination mit Wiederholung aus der Menge {1, 2, 3, 4, 5, 6} (n = 6, k = 5). Die Anzahl der möglichen Wurfergebnisse ist

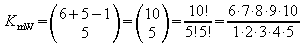4. Auf wie viele Arten können 7 Fahrräder an 7 Personen verliehen werden?

Eine Verteilung ist ein 7-Tupel, dessen Stellen mit den Personen 1 bis 7 besetzt werden.

Es liegt eine Anordnung vor; eine Wiederholung ist ausgeschlossen. Da jedes der 7 Elemente aus der Menge der Fahrräder genau einmal benutzt werden, liegt eine Permutation ohne Wiederholung vor:

5. 3 rote und 5 gelbe Tulpen sollen in 8 nebeneinander stehende Vasen gestellt werden. Wie viele verschiedene Verteilungen gibt es?

Eine Verteilung ist ein 8-Tupel, dessen Stellen mit 3 roten und 5 gelben Tulpen besetzt werden.

Durch die nebeneinander stehenden Vasen ist eine Anordnung gegeben. Alle Elemente der Menge der Tulpen werden einmal benutzt, so dass eine Permutation vorliegt. Die Vertauschungen der 3 roten Tulpen untereinander bzw. der 5 gelben Tulpen untereinander ergeben jeweils dieselbe Verteilung, so dass eine Permutation mit Wiederholung vorliegt:

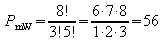6. In einem Getränkemarkt soll eine Kiste mit 12 Fruchtsaftgetränkeflaschen gefüllt werden. Es kann unter den Sorten Apfel, Birne und Orange gewählt werden. Wie viele Wahlmöglichkeiten gibt es, wenn es auf die Anordnung in der Kiste nicht ankommt?

Eine Zusammenstellung ist eine 12-Menge, deren Elemente aus Elementen der 3-Menge {Apfel, Birne, Orange} bestehen (Wiederholungen möglich).

Da die Anordnung nicht zu berücksichtigen ist, liegt eine 12-Kombination mit Wiederholung aus 3 Sorten vor. Mit n = 3 und k = 12 gibt es

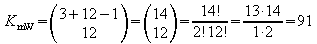
Kombinationen.

7. Auf einer Speisekarte stehen 3 Vorspeisen, 4 Hauptspeisen und 6 Nachspeisen. Wie viele verschiedene Menüs mit Vor-, Haupt- und Nachspeise lassen sich daraus zusammenstellen?

Ein Menü ist ein 3-Tupel, dessen Stellen unterschiedlich zu besetzen sind:
1. Stelle: 1 aus 3 Vorspeisen,
2. Stelle: 1 aus 4 Hauptspeisen,
3. Stelle: 1 aus 6 Nachspeisen.

Nach dem Zählprinzip ist die Anzahl der möglichen Menüs

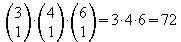8. Bei einer Prüfungsarbeit sind 5 Aufgaben zu lösen: 2 Aufgaben aus der Geometrie und 3 aus der Algebra. Aus der Geometrie sind 4 Aufgaben, aus der Algebra 6 Aufgaben zur Wahl gestellt. Wie viele Zusammenstellungen sind für die Prüfungsaufgaben möglich?

Eine Zusammenstellung ist ein 2-Tupel (Paar), dessen Stellen unterschiedlich zu besetzen sind:
1. Stelle: 2-Menge aus verschiedenen Elementen der 4-Geometrieaufgaben-Menge,
2. Stelle: 3-Menge aus verschiedenen Elementen der 6-Algebraaufgaben-Menge.
Nach dem Zählprinzip ist die Anzahl der möglichen Zusammenstellungen

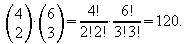Übungen

1. Aus den Buchstaben des Wortes OBERSCHLAU sollen 3 verschiedene Buchstaben ausgewählt werden, die Reihenfolge ist dabei unerheblich. Auf wie viele Arten ist dies möglich, wenn
a) die 3 Buchstaben Konsonanten sein sollen;
b) die 3 Buchstaben Vokale sein sollen;
c) 2 Buchstaben Konsonanten und 1 Buchstabe ein Vokal sein soll?

2. Das Leitungsteam eines Gymnasiums, bestehend aus Schulleiter, Stellvertreter und drei Koordinatoren stellt sich zu einem Gruppenfoto auf.
a) Wie viele Möglichkeiten sich nebeneinander aufzustellen hat das Team?
b) Der Schulleiter soll in der Mitte stehen. Wie viele Möglichkeiten gibt es jetzt?
c) Bei einer weiteren Aufnahme sollen Schulleiter und Stellvertreter nebeneinander stehen. Wie viele Aufstellungen gibt es jetzt?

3. Aus den Ziffern 3, 4, 5, 6, 7, 8, 9 sollen 5-stellige gerade Zahlen gebildet werden. Wie viele solcher Zahlen gibt es, wenn
a) die Ziffern verschieden sein sollen;
b) keine Einschränkung besteht?

4. 3 Benutzer eines Computer-Netzwerks sollen Kenn-Nummern mit 4 verschiedenen Stellen erhalten. Die Kenn-Nummern werden aus den Ziffern 1, 2, 3, 4, 5, 6 gebildet.
a) Wie viele Kenn-Nummern sind möglich?
b) Auf wie viele Arten können diese Kenn-Nummern auf die Benutzer verteilt werden?

5. In einem technischen Betrieb soll in der Forschungs- und Entwicklungsabteilung ein Entwicklungsteam mit 8 Mitgliedern zusammengestellt werden. 5 Mitglieder sollen Ingenieure und drei Mitglieder sollen Mathematiker sein. In dem Betrieb arbeiten 12 Ingenieure und 7 Mathematiker. Wie viele Zusammensetzungen des Teams sind möglich?

6. Gegeben sind die Ziffern 1, 2, ..., 6.
a) Wie viele 6-stellige Zahlen lassen sich bilden, wenn jede Ziffer in einer Zahl nur einmal auftreten soll?
b) Wie viele 3-stellige Zahlen lassen sich bilden, wenn jede Ziffer in einer Zahl nur einmal auftreten soll?
c) Sämtliche 6-stelligen aus a) seien aufsteigend der Größe nach geordnet. An welcher Stelle steht die kleinste Zahl, die mit 4 beginnt?

7. Bei einer Gesellschaft sollen 8 Personen um einen runden Tisch sitzen. Der Gastgeber probiert alle möglichen Tischordnungen durch, wobei es nicht auf den Stuhl, sondern auf die Tischnachbarn ankommt. Zwei Tischordnungen zählen also als gleich, wenn jeder dieselben Nachbarn hat. Wie viele Möglichkeiten hat der Gastgeber?

8. Eine Laplace-Münze wird 10mal geworfen, das Ergebnis ist jedesmal W oder Z. Beschreiben Sie den Ergebnisraum, wenn es
a) auf die Reihenfolge der einzelnen Ergebnisse ankommt,
b) auf die Reihenfolge nicht ankommt.
Bestimmen Sie in beiden Fällen die Mächtigkeit des Ergebnisraums. Sind die jeweiligen Elementarereignisse gleichwahrscheinlich?