Man interessiert sich hier also nicht für die möglichen 3-Tupel, die aus den Zahlen 1, 2, ..., 6 gebildet werden können, sondern für die 3-elementigen Teilmengen der Menge {1, 2, ..., 6}.
Das gleichzeitige Ziehen entspricht dem Nacheinanderziehen von 3 Kugeln ohne Berücksichtigung der Reihenfolge.
Wird zunächst die Reihenfolge berücksichtigt, so ergeben sich die 3-Variationen ohne Wiederholung der 6 Kugeln, deren Anzahl
beträgt. Jeweils 3! = 6 der 3-Variationen ohne Wiederholung führen zu der gleichen 3-elementigen Teilmenge. Es gibt also
mögliche 3-elementige Teilmengen.
2. Beim Skat erhält jeder Spieler 10 von 32 Karten. Es spielt keine Rolle, in welcher Reihenfolge man die Karten beim Austeilen erhält, da man sie nach Belieben umordnen darf. Man interessiert sich also nicht für die möglichen 10-Tupel, sondern für die 10-elementigen Teilmengen der Menge der 32 Karten.
Die Anzahl der 10-Variationen ohne Wiederholung aus der Menge der 32 Karten ist
.
Alle Permutationen eines 10-Tupels führen auf dieselbe 10-elementige Teilmenge der 32 Karten. Somit gibt es für den ersten Spieler
mögliche Kartenkombinationen.
3. Ein weiteres bekanntes Beispiel für die Auswahl von Elementen aus einer Menge ohne Wiederholung und ohne Berücksichtigung der Reihenfolge ist die Ziehung der Lottozahlen. Jede Ziehung liefert zunächst eine Menge mit 6 Elementen aus der Menge der Zahlen {1, 2, ..., 49}, und anschließend eine weitere Zahl aus den verbliebenen 43 Zahlen, die Zusatzzahl.
Aus der Zählformel für Variationen ohne Wiederholung ergeben sich zunächst
6-Tupel. Dieses Zwischenergebnis enthält aber noch alle unterschiedlichen Anordnungen von jeweils 6 Zahlen. Alle Permutationen eines 6-Tupels führen auf dieselbe 6-elementige Teilmenge. Es gibt also
mögliche Zusammenstellungen von 6 aus 49 Zahlen.
4. Allgemein: Bildet man aus einer Menge
mit n Elementen
k-elementige Teilmengen mit
und
verschiedenen Elementen, dann heißt ein solches k-Tupel eine
Kombination k-ter Ordnung von n Elementen ohne Wiederholung.
| Die Anzahl KoW
der k-Kombinationen ohne Wiederholung aus einer Menge mit n
Elementen ist
|
Die Sprechweise für die abkürzende Schreibweise
.
lautet „k aus n“, was der Lottoauswahl
„6 aus 49“ entspricht. Eine ältere Bezeichnung ist „n über
k“. Unabhängig von der Sprechweise sollte
auf
keinen Fall mit dem Bruch
verwechselt
werden.
Einige Zahlenwerte:
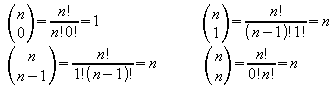
Die Zahl
wird
auch Binomialkoeffizient genannt, weil sie bei der Berechnung des
Binoms
als
Koeffizient mehrfach auftritt.
Wegen
lässt
sich die erste binomische Formel auch wie folgt schreiben:
.
Für
ergibt
sich
.
Allgemein erhält man den binomischen Lehrsatz:
.
Übungen
1. Ein Schachturnier hat 25 Teilnehmer. Es soll jeder gegen jeden spielen. Wie viele Spiele werden ausgetragen?
2. Berechnen Sie:
.
3. Vergleichen Sie:
Können Sie einen allgemeinen Zusammenhang erkennen? Wenn ja: Können Sie diesen Zusammenhang allgemein zeigen?
4. Entwickeln Sie
mit
dem binomischen Lehrsatz.
5. In den 1980er Jahren wurde ein Mittwochslotto
„7 aus 38“ angeboten. Wie viele Möglichkeiten gab es dabei, den Tippschein
auszufüllen?
Eine Urne enthält 6 nummerierte Kugeln. Es werden 3 Kugeln mit Zurücklegen gezogen; die Reihenfolge wird nicht berücksichtigt. Die Abbildung zeigt zwei mögliche Ergebnisse dieses Zufallsexperiments. Ein Pfeil verbindet eine Kugel in der Urne mit einer Kugel außerhalb der Urne, wenn diese Kugel gezogen wurde.
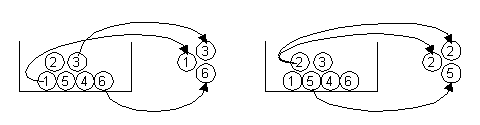
Die Umkehrung der Pfeilrichtungen lässt sich
als eine Umkehrung des Urnenmodells deuten:
3 nicht unterscheidbare Kugeln sind irgendwie
auf 6 Urnen zu verteilen. (Die Nicht-Unterscheidbarkeit entspricht der
Nicht-Berücksichtigung bei obigem Ziehen der Kugeln.)
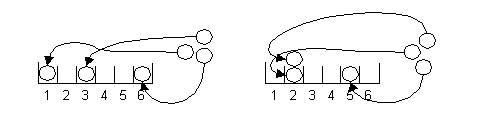
Zur Beschreibung der möglichen Verteilungen wird folgende Darstellungsweise gewählt:
Für eine Kugel wird eine „0“ geschrieben, für eine Trennwand zwischen zwei Urnen wird eine „1“ notiert. Die in der Abbildung dargestellten Verteilungen lauten in dieses Schreibweise:
01101110 bzw. 10011101.
Eine Verteilung wird also durch 8-Tupel erfasst, dessen Stellen jeweils mit 3 Nullen und 5 Einsen belegt sind.
Zunächst gibt es genau 8! verschiedene Möglichkeiten, die 8 Plätze mit 8 verschiedenen Objekten zu belegen. Nun sind die 3 Nullen aber nicht unterscheidbar; alle Belegungen, die durch Vertauschen der 3 Nullen untereinander entstehen, stellen dasselbe 8-Tupel dar; dies sind jeweils 3! verschiedene Möglichkeiten.
Auch die 5 Einsen sind nicht unterscheidbar; alle Belegungen, die durch Vertauschen der 5 Einsen untereinander entstehen, stellen ebenfalls dasselbe 8-Tupel dar; dies sind jeweils 5! verschiedene Möglichkeiten.
Somit gibt es insgesamt
verschiedene Belegungen der 8 Stellen mit 3 Nullen und 5 Einsen.
In Verallgemeinerung dieses Beispiels wird eine Urne mit n Kugeln betrachtet. Es werden k Kugeln mit Zurücklegen gezogen und die Reihenfolge wird nicht berücksichtigt. Die Umkehrung lautet: Es sollen k nicht unterscheidbare Kugeln irgendwie auf n Urnen verteilt werden.
Die möglichen Verteilungen sind in der oben beschriebenen Darstellung (k + n – 1)-Tupel, deren Stellen mit k Nullen und n – 1 Einsen zu belegen sind. Die Gesamtzahl der möglichen Verteilungen ist dann
.
| Die Anzahl KmW
der k-Kombinationen mit Wiederholung aus einer Menge mit n
Elementen beträgt
|
Übungen
1. Es werden zwei nicht unterscheidbare Würfel geworfen. Wie groß ist die Anzahl der verschiedenen Würfe?
2. Eine Dose enthält rote, grüne, weiße und blaue Gummibärchen. Aus dieser Dose sollen Tütchen mit jeweils 3 Gummibärchen gefüllt werden. Wie viele verschiedene Tütchen-Füllungen kann es geben?
.
.