12. Vektorprodukt

12.1 Definition und Rechenregeln

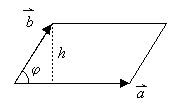
Ein Parallelogramm werde von zwei Vektoren  aufgespannt. Sein Flächeninhalt ist .

Nun ist der Winkel zwischen den Vektoren meistens nicht gegeben. Er kann zwar mit Hilfe des Skalarproduktes ermittelt werden, jedoch soll nach einem Weg gesucht werden, die Fläche des Parallelogramms direkt – also ohne Berechnung eines Winkels – aus den Koordinaten der Vektoren zu berechnen.

Mit der Identität

ergibt sich

und damit für die Parallelogrammfläche:

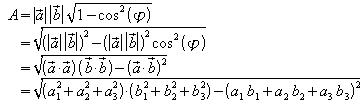
Der Radikand wird ausmultipliziert und umgeformt:

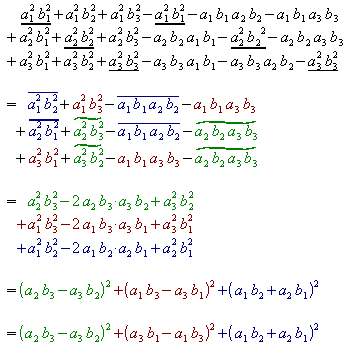
Die Fläche des Parallelogramms ist somit

Dies lässt sich deuten als der Betrag des Vektors

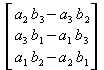Dieser Vektor wird als Vektorprodukt der Vektoren  bezeichnet. Um es vom Skalarprodukt zu unterscheiden wird es mit einem Kreuz statt des Multiplikationspunktes geschrieben:

Eigenschaften des Vektorprodukts

1. Der Betrag des Vektorproduktes ist – wie schon festgestellt wurde – gleich dem Flächeninhalt des Parallelogramms aus den Vektoren :

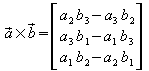2. Bildet man das Skalarprodukt vonmitbzw. mit, so ergibt sich:

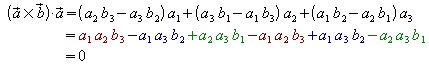
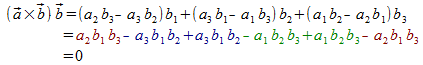
Das bedeutet, dass das Vektorprodukt senkrecht auf beiden Faktor-Vektoren steht;

3. Ohne Beweis wird noch folgende Eigenschaft des Vektorprodukts angegeben:

Die Vektoren  bilden in dieser Reihenfolge ein so genanntes Rechtssystem. Das bedeutet: Haben die Repräsentanten der Vektoren  denselben Anfangspunkt und dreht man den Vektor  in den Vektor  über den kleineren Zwischenwinkel, so bewegt man sich im Sinne einer Rechtsschraube in die Richtung des Vektors .

Rechenregeln für das Vektorprodukt

gemischtes Assoziativgesetz:

Distributivgesetz:

Anwendungen

Das Parallelogramm werde von zwei Vektoren  aufgespannt. Sein Flächeninhalt ist

also:

Der Diagonalenvektor  zerlegt das Parallelogramm in zwei kongruente Dreiecke.

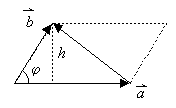
Der Flächeninhalt des Dreiecks mit den Seiten  ist daher

Volumen eines Spates

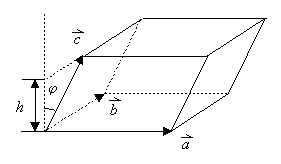
Der Spat werde von drei Vektorenaufgespannt. Sein Volumen ist

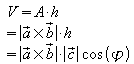also:

Dieses gemischte Produkt wird auch Spatprodukt der Vektoren  genannt.

Normalenvektor einer Ebene

Ist eine Ebene durch eine Parametergleichung  gegeben, so erhält man aus dem Vektorprodukt der Spannvektoren sofort einen Normalenvektor, da das Vektorprodukt senkrecht auf den Faktor-Vektoren steht:

Mit den beiden folgenden JavaScript-Programmen können das Vektorprodukt von zwei Vektoren bzw. das Spatprodukt von drei Vektoren berechnet werden.

Übungen

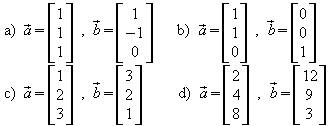
1. Berechnen Sie für die folgenden Vektoren die Vektorprodukte  und .

2. Gegeben sind die drei Vektoren.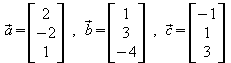

Vergleichen Sie

a),

b)

c)

3. Berechnen Sie die Flächeninhalte der Dreiecke mit folgenden Eckpunkten.

a) A(1 | 1 | 1), B(12 | 3 | 9), C(7 | 15 | 4) b) A(8 | 1 | 7), B(20 | 3 | –1), C(17 | 9 | –5)

4. Die Vektoren

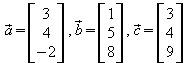
spannen einen Spat auf. Berechnen Sie

a) das Volumen des Spats,
b) die Oberfläche des Spats,
c) die Winkel zwischen den Vektoren.

5. Die Punkte A(0|0|0), B(2|0|0), C(2|2|0), D(0|2|0) sind die Eckpunkte der Grundfläche einer quadratischen Pyramide. Die Spitze ist S(1|1|5).

a) Wie lang sind die Seitenkanten?
b) Wie groß ist der Flächeninhalt je eines Seitendreiecks?
c) Wie groß ist der Neigungswinkel der Seitenflächen gegen die Grundfläche?

12.2 Lagebeziehungen von Vektoren

1. Wie schon im Abschnitt Skalarprodukt festgestellt wurde, gilt: Für zwei senkrecht stehende Vektoren ist das Skalarprodukt Null. Umgekehrt folgt für zwei vom Nullvektor verschiedene Vektoren aus dem Verschwinden des Skalarproduktes, dass die Vektoren senkrecht aufeinander stehen.

2. Zwei Vektoren, die zu einer Geraden parallel sind, heißen kollinear.

Für kollineare Vektoren gilt  . Der Winkel zwischen kollinearen Vektoren ist 0° oder 180°. In diesem Fall ist wegen  auch . Umgekehrt folgt für zwei vom Nullvektor verschiedene Vektoren aus dem Verschwinden des Vektorproduktes, dass die Vektoren kollinear sind:

3. Drei Vektoren, die zu einer Ebene parallel sind, heißen komplanar.

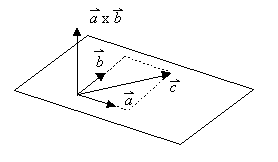
Das Vektorprodukt von je zwei dieser drei Vektoren steht senkrecht auf dieser Ebene. In diesem Fall ist das Spatprodukt der drei Vektoren Null. Umgekehrt folgt für drei vom Nullvektor verschiedene Vektoren aus dem Verschwinden des Spatproduktes, dass die Vektoren komplanar sind.

Übungen

1. a) Bestimmen Sie drei Vektoren, die senkrecht zu 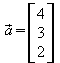 stehen.
b) Geben Sie drei zu  kollineare Vektoren an.

2. Gegeben sind die Vektoren .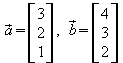
a) Bestimmen Sie drei Vektoren, die auf beiden Vektoren senkrecht stehen.
b) Geben Sie drei Vektoren an, die mit  in einer Ebene liegen.

3. Untersuchen Sie die folgenden Vektoren auf Komplanarität.

a)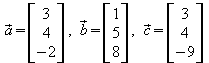

b)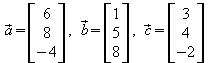

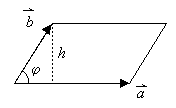
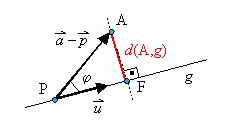
12.3 Abstand eines Punktes von einer Geraden

Wenn ein Punkt A nicht auf der Geraden  liegt, kann von A aus das Lot auf g gefällt werden. Der Fußpunkt des Lotes auf g werde mit F bezeichnet. Als Abstand des Punktes A von der Geraden g wird dann der Abstand der Punkte A und F – also die Länge der Strecke von A nach F – bezeichnet:

Aus der Zeichnung ist abzulesen:

Erweitern mit  ergibt:

Der Zähler ist aber nichts anderes als der Betrag des Vektorproduktes von . Somit ist