10. Abstandsberechnungen
10.1 Abstand zweier Punkte
Die Berechnung des Abstands zweier geometrischer
Objekte führt letztlich immer auf das Problem, den Abstand zweier
Punkte zu bestimmen. Der Abstand d(A,B) zweier Punkte A und B ist
aber einfach die Länge der Strecke 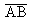 ,
oder der Betrag des Vektors
,
oder der Betrag des Vektors 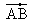 :
:
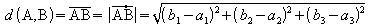
10.2 Abstand eines Punktes von einer Geraden
Um den Abstand eines Punktes P von einer Geraden 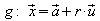 zu bestimmen, wird von P aus das Lot auf g gefällt. Der Fußpunkt
des Lotes auf g sei F. Dann ist der gesuchte Abstand gleich dem
Abstand der beiden Punkte P und F: d(P,g) =
d(P,F).
zu bestimmen, wird von P aus das Lot auf g gefällt. Der Fußpunkt
des Lotes auf g sei F. Dann ist der gesuchte Abstand gleich dem
Abstand der beiden Punkte P und F: d(P,g) =
d(P,F).
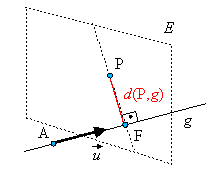
Dieser Abstand ergibt sich z.B. wie folgt:
-
Bestimmung einer zu g orthogonalen Ebene,
die durch den Punkt P verläuft:
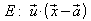 .
.
-
Bestimmung des Schnittpunktes F von g und
E.
-
d(P,g) = d(P,F).
Beispiel:
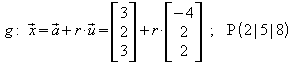
Mit dem Richtungsvektor der Geraden g als
Normalenvektor der Ebene
E ergibt sich eine Normalenform von E:
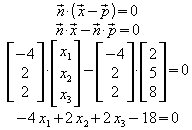
Einsetzen der Koordinaten von g:
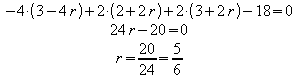
Einsetzen von r in die Gleichung von g
ergibt den Schnittpunkt F von g und E:
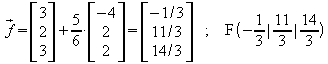
Der gesuchte Abstand ist damit
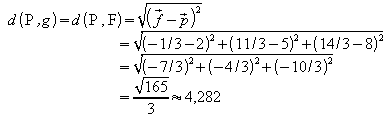
10.3 Abstand eines Punktes von einer Ebene
Wenn ein Punkt P nicht auf der Ebene 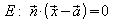 liegt, kann von P aus das Lot auf E gefällt werden. Der Fußpunkt
des Lotes auf E werde mit F bezeichnet. Als Abstand des Punktes
P von der Ebene E wird dann der Abstand der Punkte P und F bezeichnet.
liegt, kann von P aus das Lot auf E gefällt werden. Der Fußpunkt
des Lotes auf E werde mit F bezeichnet. Als Abstand des Punktes
P von der Ebene E wird dann der Abstand der Punkte P und F bezeichnet.

Dieser Abstand ergibt sich z.B. wie folgt:
-
Bestimmung einer zu E orthogonalen Gerade,
die durch den Punkt P verläuft (Lotgerade):
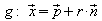 .
.
-
Bestimmung des Schnittpunktes F von g und
E.
-
d(P,E) = d(P,F).
Der Abstand kann aber auch berechnet werden, ohne
den Lotfußpunkt zu bestimmen.
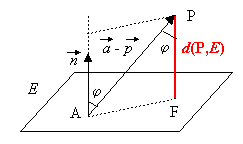
Aus dem Dreieck PFA ist abzulesen:
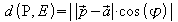
Erweitern mit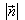 ergibt:
ergibt:
 .
.
Der Zähler ist aber nichts anderes als das
Skalarprodukt von 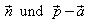 .
Somit ist
.
Somit ist
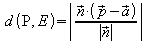
Wenn die Ebene durch eine Koordinatengleichung
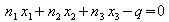
gegeben ist, ergibt sich entsprechend
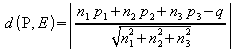 .
.
Beispiel:
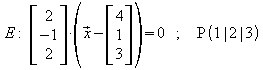
Einfaches Ausrechnen ergibt:
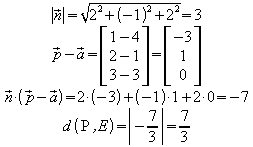
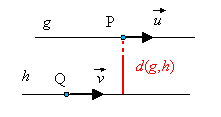
10.4 Abstand zweier paralleler Geraden
Der Abstand zweier echt paralleler Geraden g
und h mit Stützpunkten P bzw. Q ist der Abstand des Stützpunktes
der einen Gerade von der jeweils anderen Geraden.
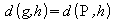
10.5 Abstand von Gerade und Ebene
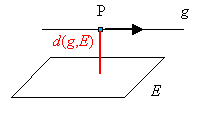
Wenn eine Gerade 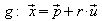 und eine Ebene E echt parallel sind, wird als Abstand von g
und E der Abstand des Stützpunktes von g von der Ebene
E bezeichnet:
und eine Ebene E echt parallel sind, wird als Abstand von g
und E der Abstand des Stützpunktes von g von der Ebene
E bezeichnet:
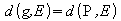 .
.
10.6 Abstand zweier Ebenen
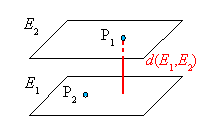
Der Abstand zweier echt paralleler Ebenen E1
und E2 mit Stützpunkten P1 bzw. P2
ist der Abstand des Stützpunktes der einen Ebene von der jeweils anderen
Ebene.
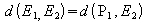
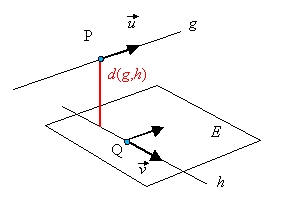
10.7 Abstand windschiefer Geraden
Unter dem Abstand zweier windschiefer Geraden
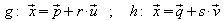
versteht man die kleinste Entfernung zwischen
den Punkten von g und den Punkten von h. Dieser Abstand ist
gleich der Länge des gemeinsamen Lotes der beiden Geraden.
Dieser Abstand ergibt sich wie folgt:
-
Konstruktion einer Hilfsebene E mit Stützpunkt
Q und Spannvektoren
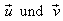 :
:
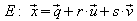 .
.
-
Berechnung des Abstands der Geraden g von
der Hilfsebene E:
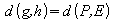
![]()
![]()

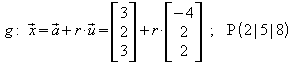
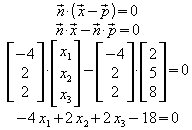
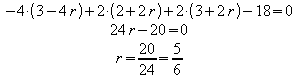
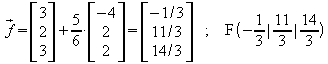
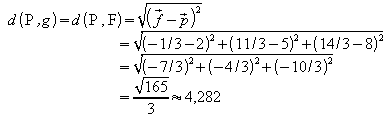


![]()
![]() ergibt:
ergibt:
![]() .
.![]() .
Somit ist
.
Somit ist
![]()
![]()
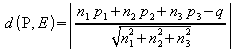 .
.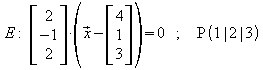
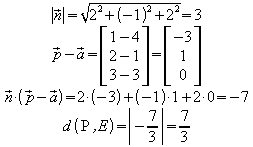

![]()

![]() .
.
![]()
![]()

![]()