,
der senkrecht auf einer Ebene E steht, heißt ein
Normalenvektor
von E.
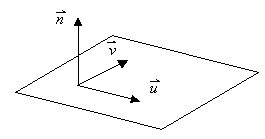
Ein Normalenvektor steht auch senkrecht auf den beiden Spannvektoren der Ebene. Daher kann bei gegebener Parametergleichung einer Ebene ein Normalenvektor durch Lösen des Gleichungssystems
berechnet werden. Zu beachten ist: Ein Normalenvektor
zu einer Ebene E lässt sich nicht in eindeutiger Weise festlegen.
Zu einem bestimmten Normalenvektor 
ist auch jedes Vielfache 
ein Normalenvektor von E.
Beispiel: Gegeben ist die Ebene E durch eine Parametergleichung:
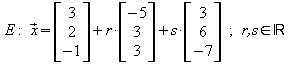
Das Gleichungssystem für einen Normalenvektor lautet:
Umformung:
Eine Koordinate kann beliebig gewählt werden, etwa
.
Dann ist
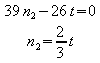
Eingesetzt in Gleichung I:
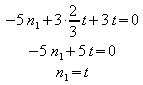
Damit hat man eine Schar von Normalenvektoren von E:
.
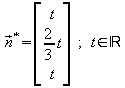Der Parameter t kann beliebig gewählt werden, um einen möglichst einfachen Vektor zu erhalten. Für t = 3 ergibt sich:
ergibt sich 
.
Mit einem Normalenvektor 
folgt weiter:
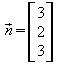
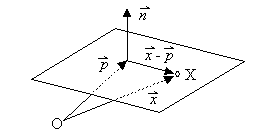
Damit hat sich eine parameterfreie Darstellung einer Ebene mit Hilfe eines Normalenvektors ergeben. Die Gleichung
nennt man eine Normalenform der Ebenengleichung.
Aus der Normalenform ergibt sich leicht die Koordinatengleichung der Ebene:
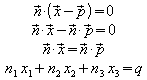
Umgekehrt lässt sich aus einer Koordinatengleichung
eine Normalenform herstellen. Setzt man 
,
dann folgt für 
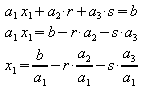
Damit ergibt sich zunächst eine Parametergleichung der Ebene:
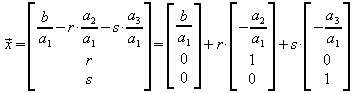
Bildet man weiter
,
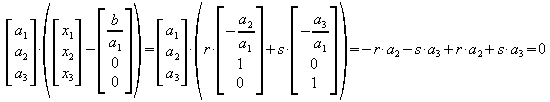so ist zu erkennen, dass die Koeffizienten der Koordinatengleichung einen Normalenvektor der Ebene bilden. Es ist also nur Schreibarbeit, aus der Koordinatengleichung eine Normalenform herzustellen:
Koordinatengleichung der Ebene: 
Normalenvektor der Ebene :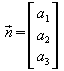 
,
Normalenform der Ebenen: 
Die folgende Abbildung fasst die Formen der Ebenengleichung und deren Umformungen zusammen.
Übungen:
1. Bestimmen Sie eine Normalenform und eine Koordinatengleichung der Ebene E.
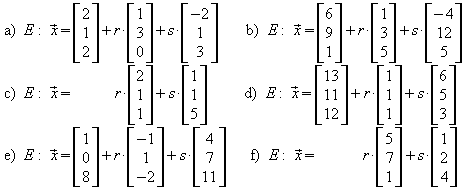
2. Geben Sie eine Normalenform der Ebene E an.
3. Geben Sie Normalenformen und Koordinatengleichungen der Koordinatenebenen an.
4. Es sei E die Ebene durch den
Punkt P(2 | –5 | 7) mit dem Normalenvektor
.
Prüfen Sie, ob der Punkt A in der Ebene E liegt.
a) A(2 | 7 | 1) b) A(0 | –1 | 7) c) A(3 | –1 | 10) d) A(4 | 6 –2)
1. Zwei Geraden sind zueinander orthogonal, wenn ihre Richtungsvektoren orthogonal sind:
.
2. Eine Gerade und eine Ebene sind zueinander orthogonal, wenn der Richtungsvektor der Geraden zu den Spannvektoren der Ebene orthogonal ist:
.
3. Zwei Ebenen sind zueinander orthogonal, wenn ihre Normalenvektoren orthogonal sind:
.
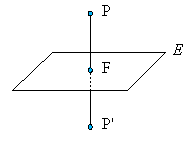
| Mit einer Geraden ,die orthogonal
zu einer Ebene ist, lässt sich die Spiegelung an einer Ebene
beschreiben. Jedem Punkt P wird ein Bildpunkt P' so zugeordnet, dass gilt:
(1) Die Gerade durch P und den Bildpunkt P' ist orthogonal zu E. (2) Der Schnittpunkt F dieser Geraden mit der
Ebene E ist Mittelpunkt der Strecke |
 |
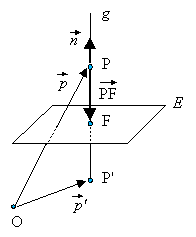
| Daraus ergibt sich folgendes praktisches
Vorgehen.
1. Der Normalenvektor von E wird als Richtungsvektor einer Geraden g verwendet, die durch P verläuft:
2. Es wird der Schnittpunkt F von g und E ermittelt. 3. Der Ortsvektor des Bildpunktes P' ergibt sich aus
|
 |
Übungen
1. Zeigen Sie: Die Gerade g und
die Ebene E sind parallel.
Wie lautet die Koordinatengleichung der zu E
parallelen Ebene durch g?
Geben Sie eine Gleichung der Geraden g2
an, die durch Spiegelung der Geraden g an der Ebene E entsteht.
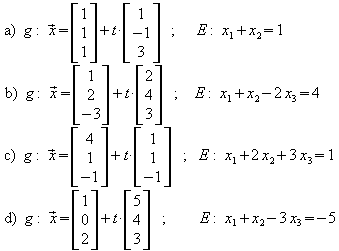
2. Gegeben sind die Gerade g und die Ebene E:
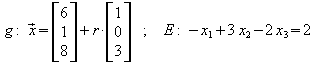
a) Zeigen Sie, dass g und E nicht orthogonal und nicht parallel zueinander sind.
b) Bestimmen Sie den Schnittpunkt S von g und E.
c) Wählen Sie beliebig einen von S verschiedenen Punkt P auf g. P wird an E gespiegelt. Bestimmen Sie den Bildpunkt P'.
d) Bestimmen Sie eine Gleichung der Bildgeraden g' bei Spiegelung von g an E.
.
.
.