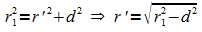Def.:
Die Menge aller Punkte X, deren Ortsvektoren 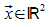 die Gleichung
die Gleichung
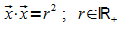
erfüllen, ist der Kreis in der x1-x2-Ebene um den Koordinatenursprung mit dem Radius r.
Zur Vereinfachung schreibt man üblicherweise 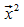 statt
statt 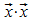 :
:
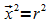
Koordinatengleichung:
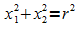
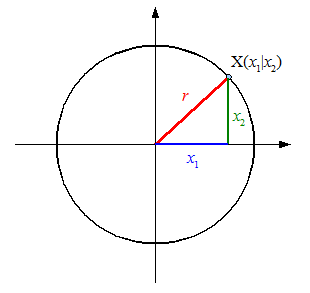
Im alltäglichen Sprachgebrauch wird "Kreis" in zwei Bedeutungen verwendet: einmal wird damit die Kreislinie bezeichnet, zum anderen aber auch die Kreisfläche. Die Mathematik benötigt eine eindeutige Definition, und unter einem Kreis soll die Kreislinie als Punktmenge verstanden werden. Diese Punktmenge wird durch eine Gleichung beschrieben.
|
Def.: Die Menge aller Punkte X, deren Ortsvektoren
erfüllen, ist der Kreis in der x1-x2-Ebene um den Koordinatenursprung mit dem Radius r. Zur Vereinfachung schreibt man üblicherweise
Koordinatengleichung:
|
|
Ist der Mittelpunkt eines Kreises vom Koordinatenursprung O(0|0) verschieden, so haben die Ortsvektoren der Punkte des Kreises keine einheitliche Länge. Es gilt aber immer noch, dass der Abstand jedes Punktes X des Kreises vom Mittelpunkt M konstant, und zwar gleich dem Radius ist.
Ist
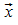 der
Ortsvektor des Punktes X und
der
Ortsvektor des Punktes X und 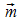 der Ortsvektor des Mittelpunktes M, dann ist
der Ortsvektor des Mittelpunktes M, dann ist 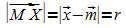 .
.
|
Def.: Sei
erfüllen, ist der Kreis in der x1-x2-Ebene um den Mittelpunkt M mit dem Radius r. Koordinatengleichung:
|
|
Eine Kugel, im Sinne von Kugelfläche, wird als Menge aller Punkte des Raumes definiert, die von einem fest vorgegebenen Punkt M einen festen Abstand r haben.
Def.:
Sei 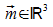 der Ortsvektor eines Punktes M im Raum. Die Menge aller Punkte X,
deren Ortsvektoren
der Ortsvektor eines Punktes M im Raum. Die Menge aller Punkte X,
deren Ortsvektoren 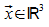 die Gleichung
die Gleichung
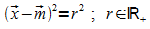
erfüllen, ist die Kugel um den Mittelpunkt M mit dem Radius r.
Koordinatengleichung:
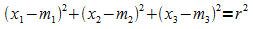
Jeder
Punkt P der Kugel lässt sich durch seine kartesischen
Koordinaten (x1; x2; x3)
eindeutig
beschreiben.
Häufig ist es aber sinnvoller, die
sogenannten Kugelkoordinaten 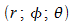 zu verwenden. Diese sind wie folgt definiert.
zu verwenden. Diese sind wie folgt definiert.
|
|
Die Kugelkoordinaten und die kartesischen Koordinaten können ineinander umgerechnet werden:
|
Im Dreieck OPF findet sich der Winkel
Wird
Zusammengefasst:
|
|
Für die Berechnung der Kugelkoordinaten aus den kartesischen Koordinaten liest man ab:
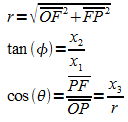
also:
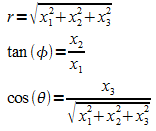
Speziell
zur Orientierung auf der Erdoberfläche sind anstelle der
Kugelkoordinaten die geographischen Koordinaten 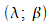 gebräuchlich. Diese sind wie folgt definiert:
gebräuchlich. Diese sind wie folgt definiert:
Die geographische Breite 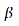 (Breitengrade) wird vom Äquator aus gezählt, die
Pole
liegen bei
(Breitengrade) wird vom Äquator aus gezählt, die
Pole
liegen bei 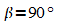 (Nord) bzw.
(Nord) bzw. 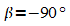 (Süd);
(Süd);
die geographische Länge 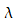 (Längengrade) wird von einem willkürlichen
Nullmeridian (Meridian von Greenwich) nach Osten (
(Längengrade) wird von einem willkürlichen
Nullmeridian (Meridian von Greenwich) nach Osten (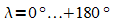 )
und Westen (
)
und Westen (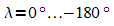 )
gezählt.
)
gezählt.
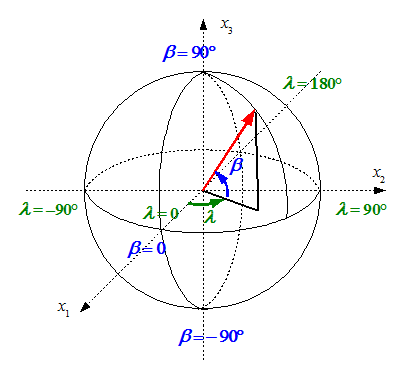
Aus den geographischen Koordinaten erhält man mit dem Erdradius rE die Koordinaten eines Punktes auf der Erdoberfläche:
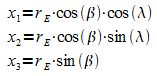
Beispiel:
Für Hamburg ist 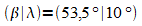 .
Dies
ergibt
.
Dies
ergibt
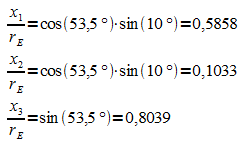
Gegeben
sind eine Kugel K mit Mittelpunkt M und Radius r, sowie
ein Punkt 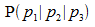 .
Die
zu M und P gehörigen Ortsvektoren sind
.
Die
zu M und P gehörigen Ortsvektoren sind 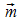 und
und 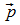 .
.
Bei
der Punktprobe für P wird 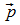 für
für 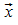 in die Vektorgleichung der Kugel oder die Koordinaten von P in die
Koordinatengleichung der Kugel eingesetzt.
in die Vektorgleichung der Kugel oder die Koordinaten von P in die
Koordinatengleichung der Kugel eingesetzt.
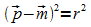 bzw.
bzw. 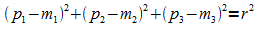 :
P liegt auf der Kugel K
:
P liegt auf der Kugel K
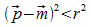 bzw.
bzw.
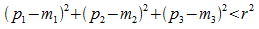 :
P liegt innerhalb der Kugel K
:
P liegt innerhalb der Kugel K
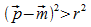 bzw.
bzw. 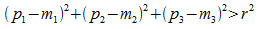 :
P liegt außerhalb der Kugel K
:
P liegt außerhalb der Kugel K
Für eine Gerade und eine Kugel gibt es drei verschiedene Lagebeziehungen:
|
Die Gerade ist Sekante. |
Die Gerade ist Tangente. |
Die Gerade ist Passante. |
|
|
||
Gegeben
sind eine Gerade 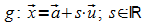 und eine Kugel K mit Mittelpunkt M und Radius r. Die
Punktprobe für die Punkte von g in der Gleichung von K
liefert eine quadratische Gleichung für den Parameter s:
und eine Kugel K mit Mittelpunkt M und Radius r. Die
Punktprobe für die Punkte von g in der Gleichung von K
liefert eine quadratische Gleichung für den Parameter s:
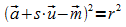 bzw.
bzw. 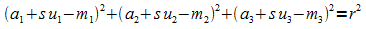
Besitzt sie
zwei Lösungen, so haben g und K zwei Punkte S1 und S2 gemeinsam. Die Gerade g ist eine Sekante.
genau eine Lösung, so berührt g die Kugel K in einem Punkt B. Die Gerade g ist eine Tangente.
keine Lösung, so haben g und K keine gemeinsamen Punkte. Die Gerade g ist eine Passante.
Für eine Ebene und eine Kugel gibt es drei verschiedene Lagebeziehungen:
|
Die Ebene schneidet die Kugel in einem Kreis. |
Die Ebene berührt die Kugel in einem Punkt. |
Die Ebene und die Kugel schneiden sich nicht. |
|
|
||
Gegeben
sind eine Ebene 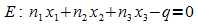 und eine Kugel mit Mittelpunkt M und Radius r. Der Abstand des
Mittelpunktes M von der Ebene E ergibt sich aus
und eine Kugel mit Mittelpunkt M und Radius r. Der Abstand des
Mittelpunktes M von der Ebene E ergibt sich aus
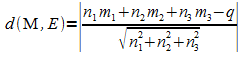
(siehe Abschnitt "Ebenen"). Ist dieser Abstand
kleiner als der Radius r, so besitzen E und K einen gemeinsamen Schnittkreis k.
gleich dem Radius r, so besitzen E und K genau einen gemeinsamen Punkt, den Berührpunkt B. Die Ebene E ist dann eine Tangentialebene der Kugel K.
größer als der Radius r, so besitzen E und K keine gemeinsamen Punkte.
Zur Berechnung eines Schnittkreises wird wie folgt vorgegangen:
Es wird die Gleichung der Lotgeraden g durch den
Kugelmittelpunkt M mit dem Normalenvektor 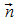 von E als Richtungsvektor aufgestellt:
von E als Richtungsvektor aufgestellt:
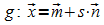
Zur Berechnung des Schnittpunktes von Lotgerade g und Ebene E wird in bekannter Weise der Geradenterm in die Ebenengleichung eingesetzt und die resultierende Gleichung nach dem Parameter s aufgelöst:
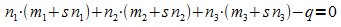
Einsetzen des gefundenen Wertes für s in die Gleichung
der Lotgeraden ergibt den Ortsvektor 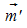 des Schnittkreismittelpunktes M ':
des Schnittkreismittelpunktes M ':
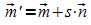
Der Radius r' des Schnittkreises ergibt sich mit dem
Kugelradius r und dem Abstand 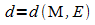 nach dem Satz des Pythagoras:
nach dem Satz des Pythagoras:
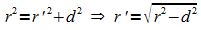
Ein
Berührpunkt von E und K wird entsprechend als
Schnittpunkt der Lotgeraden 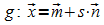 mit der Ebene E berechnet.
mit der Ebene E berechnet.
Bei zwei Kugeln gibt es 6 verschiedene Lagebeziehungen.
Gegeben sind zwei Kugeln K1 und K2 mit den Mittelpunkten M1 und M2 und den Radien r1 und r2. Die Kugeln K1 und K2
besitzen einen Schnittkreis k für 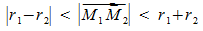 .
.
berühren sich für 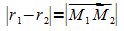 von innen und für
von innen und für 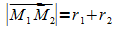 von außen.
von außen.
liegen für 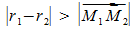 ineinander und für
ineinander und für 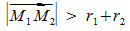 auseinander.
auseinander.
Die Berechnung eines Schnittkreises soll kurz skizziert werden.
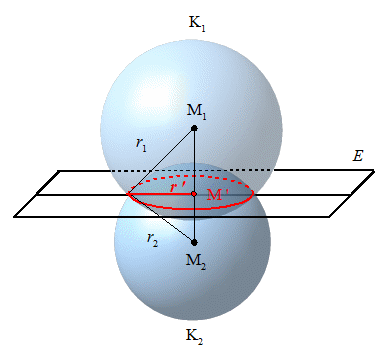
Gegeben seien zwei Kugeln durch ihr Koordinatengleichungen:
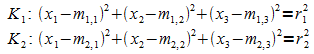
Die beiden Koordinatengleichungen werden subtrahiert. Als
Ergebnis erhält man die Ebenengleichung der Schnittkreisebene 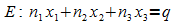 .
.
Es wird die Gleichung der Lotgeraden g durch den
Kugelmittelpunkt M1 mit dem Normalenvektor 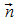 von E als Richtungsvektor aufgestellt:
von E als Richtungsvektor aufgestellt: 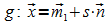 .
.
Die Berechnung des Schnittpunkts von g und E ergibt den Mittelpunkt M ' des Schnittkreises.
Mit dem Kugelradius r1 und dem Abstand 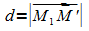 ergibt sich der Radius des Schnittkreises nach dem Satz des Pythagoras:
ergibt sich der Radius des Schnittkreises nach dem Satz des Pythagoras: