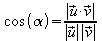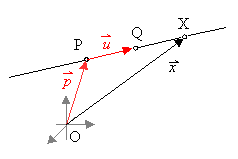
(und
damit seine Koordinaten) bestimmen?
Die Skizze lässt erkennen, wie diese Bestimmung von
erfolgt.
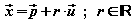
Die reelle Zahl r nennt man in diesem Zusammenhang
Parameter.
Eine Darstellung wie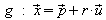
heißt
deswegen
auch
Parameterdarstellung (oder Parametergleichung)
der Geraden g.
heißt
Stützvektor
und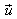
Richtungsvektor
von g. Zu jedem Parameterwert r gehört genau ein
Punkt
X der Geraden, und umgekehrt gehört zu jedem Punkt X der Geraden
genau
eine reelle Zahl r.
Ist eine Gerade durch zwei Punkte P und Q (mit den Ortsvektoren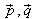
)
gegeben, so ist
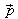ein
Stützvektor und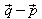
ein
Richtungsvektor.
Beispiel: P(1 | 5 | –4) , Q(4 | 3 | –1)
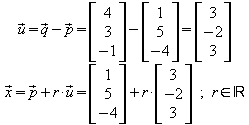
Ortsvektoren weiterer Punkte auf der Geraden durch P und Q sind z.B.
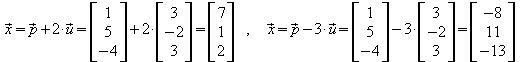
Übungen:
1. Geben Sie je zwei verschiedene Parameterdarstellungen der Geraden g durch die Punkte A und B an.
a) A( 2 | 1 ) , B( 5 | 0) b) A( –3 | 2 ) , B( 1 | 1 )
c) A( 1 | 2 | 3 ) , B( –4 | 0 | 5 ) d) A( 2 | 0 | 1) , B(1 | 9 | –3 )
2. Geben Sie zur Geraden g eine Parameterdarstellung der zu g parallelen Geraden durch den Punkt P( 2 | –3 | 7 ) bzw. Q( 1 | 1 | –8 ) an.
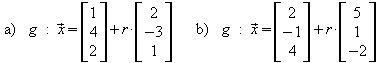
Beispiel 1: Liegt A(3 | 5 | –2) auf der Geraden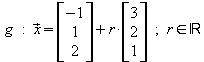
?
Wenn ja, dann müsste der zu A gehörende Ortsvektor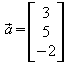
die
Geradengleichung erfüllen, d.h. es müsste eine reelle Zahl
r
geben, für die gilt:
.
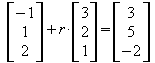Die Vektorgleichung ist gleichbedeutend mit dem System der Koordinatengleichungen
Die erste Gleichung ist nur für r = 4/3, die zweite nur für r = 2, die dritte nur für r = –4 erfüllt. Es gibt also keine Zahl r, für die alle drei Gleichungen zugleich erfüllt sind. Das bedeutet: A liegt nicht auf g.
Beispiel 2: Liegt A(–2 | 3 | –4) auf der Geraden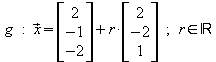
?
Eine Rechnung wie im ersten Beispiel führt auf das System der Koordinatengleichungen
Alle drei Gleichungen sind für r = –2 erfüllt. A liegt also auf der Geraden g.
Übung:
Prüfen Sie, ob der Punkt X auf der Geraden g liegt.
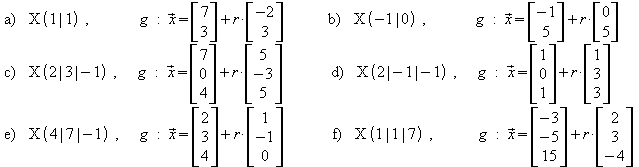
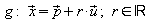liegt,
kann von A aus das Lot auf g gefällt werden. Der
Fußpunkt
des Lotes auf g werde mit F bezeichnet. Als Abstand des Punktes
A von der Geraden g wird dann der Abstand der Punkte A und F –
also
die Länge der Strecke von A nach F – bezeichnet:
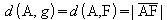
Aus der Zeichnung ist abzulesen:
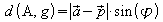
Erweitern mit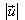
ergibt:
.
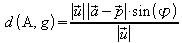Der Zähler ist aber nichts anderes als der Betrag des
Vektorproduktes
von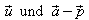 
.
Somit ist
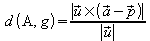
Das folgende JavaScript-Programm ermöglicht die Berechnung des Abstandes eines Punktes von einer Geraden.
Übungen:
1. Berechnen Sie jeweils den Abstand des Punktes A von der Geraden g.
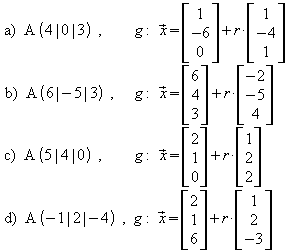
2. Berechnen Sie in der Übung zur „Punktprobe“ im vorigen Abschnitt jeweils den Abstand des Punktes X von der Geraden g.
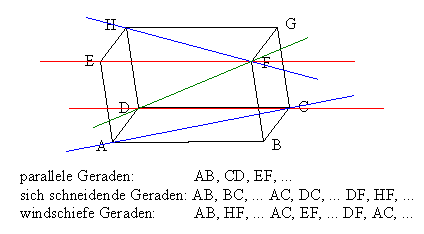
Für zwei Geraden im Raum gibt es vier Möglichkeiten für ihre gegenseitige Lage:
In der folgenden Abbildung sind einige Geraden in einen Quader
eingezeichnet,
die diese Lagen verdeutlichen.
Die Geraden seien durch ihre Parametergleichungen gegeben:
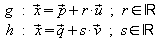
Die Fälle 1 und 2 lassen sich auf den ersten Blick von den
Fällen
3 und 4 unterscheiden:
| Bei parallelen Geraden
(zusammenfallend oder
echt parallel) sind die Richtungsvektoren kollinear:
Unterscheidung der Fälle: Die Vektoren
|
Bei nicht-parallelen Geraden
(schneidend oder
windschief) sind die Richtungsvektoren nicht kollinear:
Unterscheidung der Fälle: Die Vektoren
|
||
| sind kollinear:
|
sind nicht kollinear:
|
sind komplanar:
|
sind nicht komplanar:
|
Beispiel 1: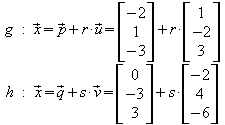
Wie sofort zu erkennen ist, sind die Richtungsvektoren kollinear: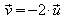
.
g
und h sind also parallel.
Weiter sind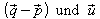
kollinear:
;
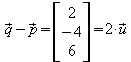g
und h fallen also zusammen.
Beispiel 2: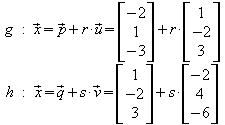
Die Richtungsvektoren sind kollinear: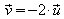 
.
g
und h sind also parallel.
Für die Vektoren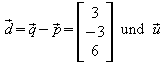
gilt:
;
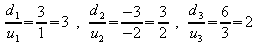sie sind nicht kollinear; g und h sind also echt
parallel.
Der Abstand der Geraden ist der Abstand des Stützpunktes P der Geraden g von der Geraden h oder der Abstand des Stützpunktes Q der Geraden h von der Geraden g.
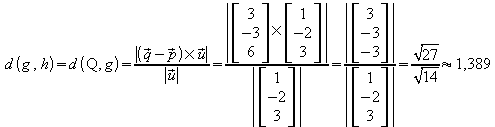
oder:
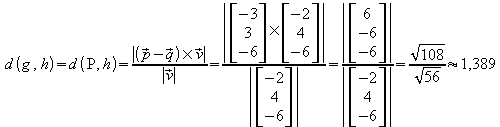
Beispiel 3: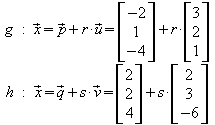
Für die Richtungsvektoren gilt: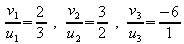
,
sie sind nicht kollinear , und daher sind g und h nicht
parallel.
Das Spatprodukt aus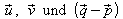
ist
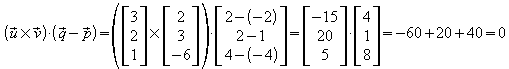
Die Vektoren sind komplanar, die Geraden g und h schneiden sich in genau einem Punkt.
Der Schnittpunktansatz
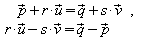
führt auf das Gleichungssystem
Aus Gleichung II'' folgt s = 1;
einsetzen in Gleichung I'': r + 6s =
8
r + 6 = 8
r = 2
Der Schnittpunkt S wird erhalten, indem der Parameterwert für r in die Gleichung von g oder der Parameterwert von s in die Gleichung von h eingesetzt wird:
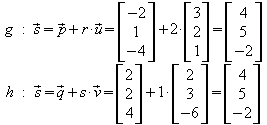
Der Schnittpunkt ist also S( 4 | 5 | -2).
Beispiel 4:
Wie in Beispiel 3 ergibt eine einfache Rechnung wieder, dass die Richtungsvektoren nicht kollinear sind. Die Geraden sind also nicht parallel.
Das Spatprodukt aus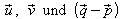
ist
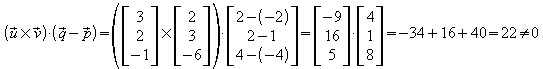
Die Vektoren sind nicht komplanar; die Geraden g und h sind also windschief.
(Anmerkung: Der Abstand windschiefer Geraden kann an dieser Stelle noch nicht ermittelt werden. Dazu wird die Darstellung von Ebenen im Raum benötigt, die erst im folgenden Kapitel entwickelt wird.)
Das folgende JavaScript-Programm ermöglicht die Untersuchung der gegenseitigen Lage zweier Geraden in der Ebene bzw. im Raum.
Übungen:
1. Untersuchen Sie die Lage der Geraden AB und CD (AC und CD)
zueinander.
Falls die Geraden (echt) parallel sind, ermitteln Sie den Abstand der
beiden Geraden.
Für den Fall des Schneidens geben Sie den Schnittpunkt an.
a) A(1 | 0 | 5) , B(5 | –2 | 11) , C(3 | –1 | 8) , D(–1 | 1 | 2)
b) A(0 | 0 | 0) , B(3 | 2 | 1) , C(3 | 0 | 0) , D(0 | 2 | 1)
c) A(0 | 0 | 2) , B(1 | 3 | 0) , C(0 | 2 | 0) , D(2 | 0 | 0)
2. Untersuchen Sie die Lage der Geraden g und h
zueinander.
Berechnen Sie im Fall des Schneidens den Schnittpunkt und im Fall
paralleler
Geraden den Abstand.
3. Prüfen Sie, ob sich die Geraden g und h in den folgenden Abbildungen schneiden. (E und F sind Kantenmitten.)
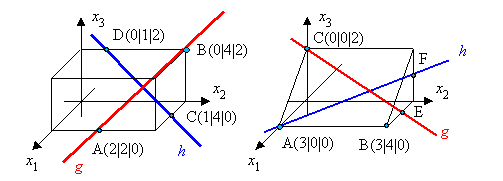
4. Gegeben sind die Punkte A( 5 | 2 | 0 ) , B( 1 | 2 | 1 ) , C( 1 | 1 | 0 ) und D( 2 | 3 | 0 ).
a) Zeigen Sie, dass die Geraden AB und CD windschief zueinander sind, dass also ABCD ein nichtebenes Viereck ist.
b) Zeigen Sie, dass die Geraden durch die Mittelpunkte gegenüberliegender Seiten sich in einem Punkt schneiden. Berechnen Sie den Schnittpunkt.
c) Zeigen Sie, dass die Mittelpunkte der Seiten ein Parallelogramm bilden.
d) Prüfen Sie, ob die Diagonalen des Vierecks sich in einem Punkt schneiden.
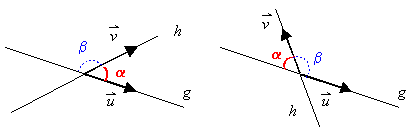
Wenn sich zwei Geraden g und h schneiden, so ergeben
sich
zwei Winkel: Ein Wink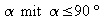el 
und
ein
Winkel
.
Als Schnittwinkel wird der Winkel
bezeichnet.
Er
ergibt
sich aus dem Skalarprodukt der beiden Richtungsvektoren der
Geraden:
.
