4. Verknüpfungen von Vektoren

4.1 Addition von Vektoren

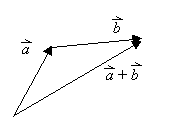
Verschiebungen können nacheinander ausgeführt werden. Je zwei Verschiebungen lassen sich zu einer resultierenden Verschiebung zusammenfassen (verketten).

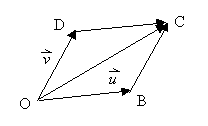
Da einer Verschiebung eindeutig ein Vektor zugeordnet ist, lassen sich auch je zwei Vektoren verketten. Von zwei Vektoren wählt man einen Repräsentanten des Vektors und einen Repräsentanten des Vektors , dessen Anfangspunkt an der Spitze von liegt.
 Dies führt zur Definition der Addition von Vektoren: zwei Vektoren werden addiert, indem man sie verkettet.

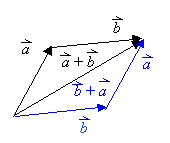
Die Bezeichnung „Addition“ ist gerechtfertigt, da für diese Verkettung von Vektoren dieselben Rechengesetze gelten wie für die Addition reeller Zahlen:
 

Kommutativgesetz:

Assoziativgesetz: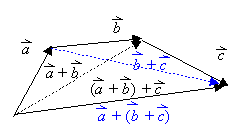

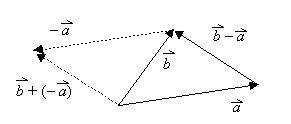
Unter Verwendung des Gegenvektors lässt sich auch die Subtraktion von Vektoren erklären:

Um einen Vektor zu subtrahieren ist sein Gegenvektor zu addieren.

Die Subtraktion ist – wie bei reellen Zahlen – nicht kommutativ:

• ein Repräsentant vonweist von der Spitze vonzur Spitze von;
• ein Repräsentant vonweist von der Spitze vonzur Spitze von.

Addition mit Hilfe der Koordinaten

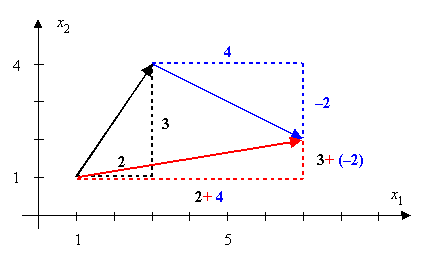
Ein Beispiel lässt erkennen, wie die Addition von Vektoren unter Verwendung ihrer Koordinaten durchzuführen ist:

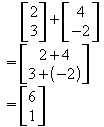
Allgemein gilt: Bei der Addition von Vektoren sind die entsprechenden Koordinaten zu addieren.

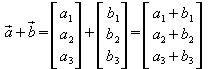
Um den Gegenvektor zu einem Vektor zu erhalten, werden die Vorzeichen der Koordinaten umgekehrt:

Für die Subtraktion zweier Vektoren folgt also:

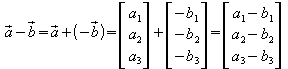Übungen:

1.  Berechnen Sie:

2.

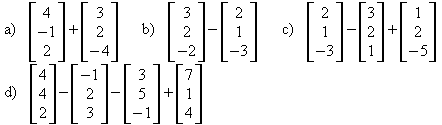
3.  Lösen Sie die Vektorgleichungen.

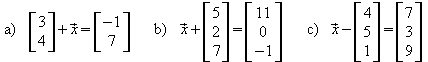
Anwendung

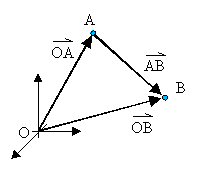
Jeder Vektorkann durch die Ortsvektorenundausgedrückt werden:

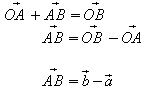
Übungen:

4.  Berechnen Sie für die Punkte A(2 | –1 | 5), B(3 | 0 | 3), C( –2 | 7 | 1), D(4 | 4 | 4) die Koordinaten von

5.  Der Vektorbildet den Punkt P auf den Punkt Q ab, der Vektorbildet P auf R ab. Auf welchen Punkt wird P vonabgebildet?

        a) P( 2  |  7  | –1) , Q( 3  | –5  |  9 ) , R( 2  |  6  | –5 )             b) P( 11  |  0  | –2 ) , Q( 8  |  13  | –5 ) , R( 5  |  6  |  7)

Java-Applets für interaktive Übungen:

Addition von Vektoren

Subtraktion von Vektoren

3-Vektoren kennenlernen: 2) Addition und Subtraktion

Verknüpfungen von Vektoren im regelmäßigen Sechseck
 

Weiterführende Übungen

W1. Gegeben sind die Vektoren. Veranschaulichen Sie in einer Zeichnung die Vektor-Addition. Konstruieren Sie dabei auch das Parallelogramm, das die Kommutativitätveranschaulicht.

Welche Eingaben sind in DERIVE nötig, um das Parallelogramm zu zeichnen?
 

W2. Ein Viereck ABCD ist ein Parallelogramm, wenn odergilt.
 Prüfen Sie für folgende Punkte, ob ein Parallelogramm vorliegt und zeichnen Sie.

 a)  A(4 | 2) , B(6 | 3) , C(7 | 7) , D(5 | 6)

 b)  A(–3 | 1) , B(1 | 1) , C(6 | 4) , D(2 | 4)

 c)  A(–3 | –3) , B(2 | –2) , C(5 | 1) , D(1 | 6)
 

W3. Bestimmen Sie einen Punkt D so, dass das Viereck ABCD ein Parallelogramm ist und zeichnen Sie.

 a)  A(2 | 4 | 1) , B(3 | –1 | 3) , C(4 | –2 | 3)

 b)  A(5 | 2 | 4) , B(2 | –2 | 1) , C(3 | 6 | 2)
 

W4. Zwei Vektoren „spannen ein Parallelogramm auf“. Damit ist gemeint, dass sich das Parallelogramm aus der Addition der beiden Vektoren ergibt:

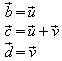
Die räumliche Entsprechung zu einem Parallelogramm ist ein Spat . Ein Spat wird von 3 Vektoren aufgespannt.

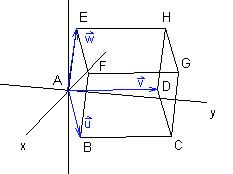
a) Es sei A(0 | 0 | 0). Dann gilt:

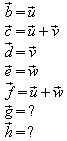
Gegeben sind die Vektoren.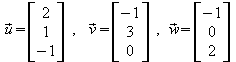

Berechnen Sie die Koordinaten aller Eckpunkte und zeichnen Sie den Spat.

b) Wie erhält man die Eckpunkte, wenn A nicht im Koordinatenursprung liegt?

c) Wie kann der Spat in DERIVE gezeichnet werden?

4.2 Multiplikation von Vektoren mit reellen Zahlen (Vervielfachen von Vektoren)

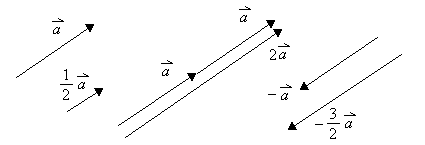
Für einen Vektorund eine reelle Zahlist das Produkt(das „r-fache von“) ein Vektor mit den Eigenschaften

• die Pfeile vonsind parallel zu den Pfeilen von;
• für r > 0 sind die Pfeile vonundgleich gerichtet;
• für r < 0 sind die Pfeile vonundentgegengesetzt gerichtet;
• die Länge der Pfeile vonist das | r |-fache der Länge der Pfeile von.

Für r = 0 wird festgelegt: .

Multiplikation von Vektoren mit reellen Zahlen in Koordinaten

Ein Beispiel lässt erkennen, wie diese Multiplikation in Koordinaten auszuführen ist:

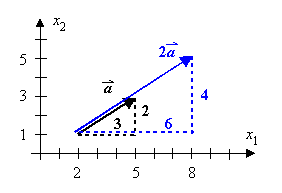
Allgemein gilt:

 Ein in Koordinaten gegebener Vektor wird mit einer reellen Zahl r multipliziert, indem man seine Koordinaten mit r multipliziert:

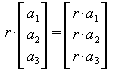
Aus dieser Definition ergeben sich folgende Rechenregeln.

Diese Regeln ergeben sich aus den Definitionen der Vektoraddition und der Multiplikation mit einer reellen Zahl sowie den Rechengesetzen für reelle Zahlen.

Nachweis des Distributivgesetzes für r :

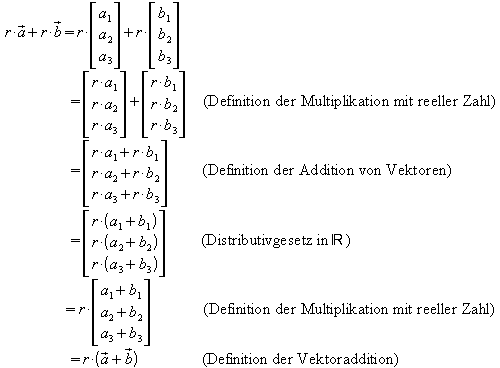
Das Distributivgesetz fürund das gemischte Assoziativgesetz sind ebenso durch einfaches Nachrechnen zu bestätigen.

Übungen:

Die folgenden Übungen sind dem verwendeten Lehrbuch zu entnehmen. Als Beispiel wird hier jeweils die erste Teilaufgabe vorgeführt.

1.  S.17, Nr. 4: a) 

2.  S.17, Nr.5: a) 

3.  S.17, Nr.6: a)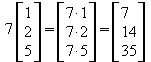 

4.  S.17, Nr.7: a)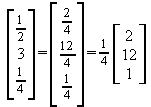 

5.  S.17, Nr.8 a)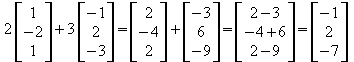 

6.  S.17, Nr.9 a)

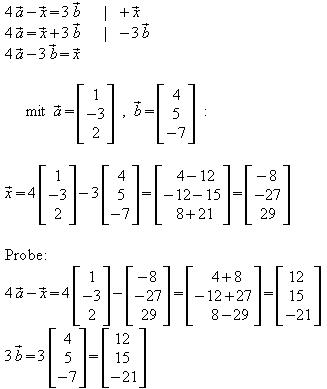
Anwendungen

1. Streckenmittelpunkte

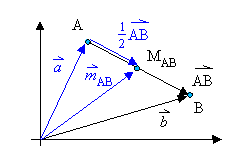
Eine Streckewird nach Festlegung einer Orientierung zu einem Pfeil. Der Streckenmittelpunkt M_AB liegt in der Mitte des Pfeils, und es ist . Der Ortsvektor von M_AB ergibt sich aus

.

Unter Verwendung der Ortsvektoren der Punkte A und B ergibt sich daraus

.

Beispiel: Ein Dreieck ABC hat die Eckpunkte A( 2 | 2), B(10, | 0), C(6 | 6). Es sollen die Ortsvektoren der Seitenmittelpunkte angegeben werden.

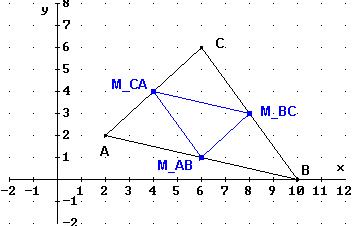
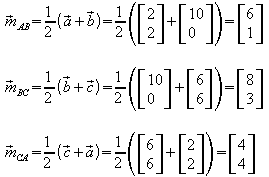
Die Zeichnung lässt vermuten, dass die Verbindungsstrecken von je zwei Seitenmittelpunkten parallel zu den gegenüberliegenden Dreiecksseiten sind. Dies kann rechnerisch überprüft werden.
 Für den durch M_CA und M_BC definierten Vektor gilt:

Ein Vergleich mit

zeigt:

.

Die Streckeist also parallel zur Dreiecksseiteund halb so lang wie diese.

Entsprechend ist nachzurechnen:

.

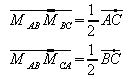2. Zentrische Streckung
 

Eine zentrische Streckung mit dem Zentrum Z und dem Streckfaktor k ist eine Abbildung der Ebene auf sich selbst mit folgenden Eigenschaften. Z ist Fixpunkt der Abbildung. Ist P ¹ Z, so liegt das Bild P' von P auf der Geraden durch Z und P. k > 0: P und P' liegen auf derselben Seite von Z; k < 0: P und P' liegen auf verschiedenen Seiten von Z. Für Bild P' und Urbild P gilt: .
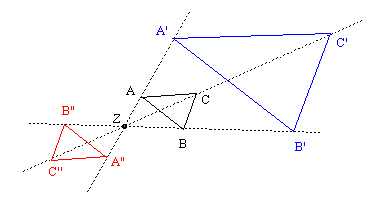a) zentrische Streckung mit Z = O (Koordinatenursprung): Hier gilt für die Ortsvektoren von Punkten, die zentrisch gestreckt werden, einfach:
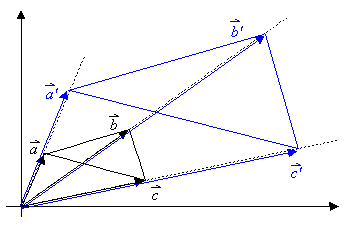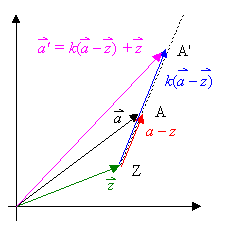
b) zentrische Streckung mit Z ¹ O: Hier sind nicht die Ortsvektorenvon Punkten P mit dem Streckfaktor k zu multiplizieren sondern die Differenzvektoren. Um den Ortsvektor des Bildpunktes P' zu erhalten, ist dann noch der Ortsvektor von Z zu addieren:

3. Linearkombination von Vektoren

Für k Vektorenund k reelle Zahlennennt man

eine Linearkombination der Vektoren.

Häufig tritt das Problem auf, einen gegebenen Vektor als Linearkombination einer Menge anderer Vektoren darzustellen.
Beispiel 1: Der Vektorist als Linearkombination der Vektorendarzustellen. Es sind also reelle Zahlen r, s gesucht, s dass gilt

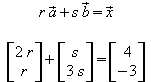
Diese Vektorgleichung entspricht zwei linearen Gleichungen für die Unbekannten r und s:

Aus der zweiten Gleichung folgt

;

dies wird in die erste Gleichung eingesetzt:

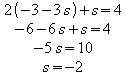
Für r ergibt sich damit:

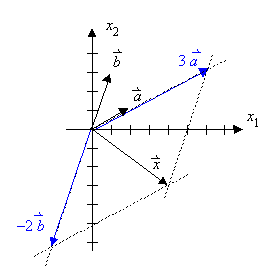
Die gesuchte Linearkombination ist also

Probe:

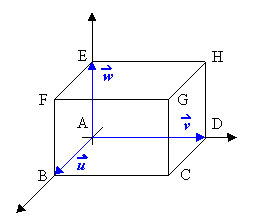
Beispiel 2: Kantenvektoren von Körpern

Quader:
 

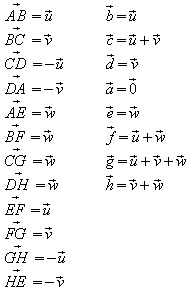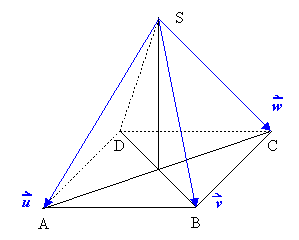
quadratische Pyramide:
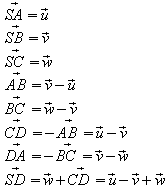