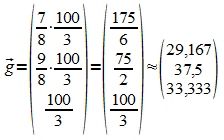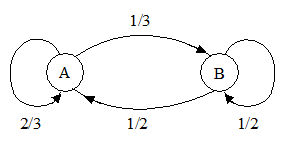
1. In einer Betriebskantine werden mittags zwei Arten von Gerichten angeboten: A: fleischhaltig, B: rein vegetarisch. Die Gäste der Kantine zeigen folgendes Verhalten: Von den Gästen, die das Gericht der Art A gewählt haben, wählen beim nächsten Ma(h)l zwei Drittel wieder das Gericht der Art A, während ein Drittel zum Gericht der Art B wechselt. Gäste, die B gewählt haben, wechseln beim nächsten Mal zur Hälfte zu A, während die andere Hälfte wieder B wählt. Im Folgenden wird vorausgesetzt, dass sich von einem Tag zum nächsten die Anzahl der Gäste nicht verändert.
Übergangsdiagramm:
Die Anzahl der Wahlen von A am ersten Tag wird mit x1 bezeichnet, die Anzahl am zweiten Tag mit y1. Entsprechend werden die Anzahlen der Wahlen von B mit x2 bzw. y2 bezeichnet. Der Übergang von einem Tag zum nächsten wird dann durch folgende Gleichung beschrieben:
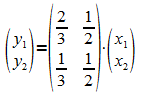
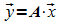
Nach Voraussetzung ändert sich die Anzahl der Gäste
nicht, und es liegt nur eine Neuverteilung einer Gesamtzahl von
Gästen auf die Wahlmöglichkeiten A und B vor. Somit ist die
Summe aller Eingangswerte gleich der Summe aller Ausgangswerte: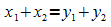 
.
Im Beispiel sei die Anzahl von Gästen 900. Für die
Anfangsverteilung 
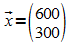ergibt sich am folgenden Tag die Verteilung:
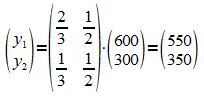
Die Matrix A, die den Austauschprozess beschreibt, besitzt die Eigenschaft, dass die Summe der Elemente einer Spalte 1 ergibt. Ein solcher Prozess wird Austauschprozess genannt. Allgemein:
|
Definition: Ein Prozess, der durch eine
quadratische Matrix |
Für die Planung des Kantinenbetriebs ist die Frage
interessant, ob es eine Verteilung 
gibt, die sich nicht mehr verändert, für die also gilt:
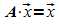
Als Gleichungssystem geschrieben:
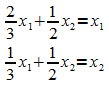
umgeformt:
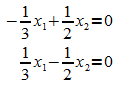
Die Addition der beiden Gleichungen ergibt eine Nullzeile, d.h. das homogene Gleichungssystem besitzt eine nicht-triviale Lösung. Aus der zweiten Gleichung ergibt sich
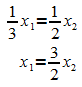
Die Lösungsmenge des Gleichungssystems ist somit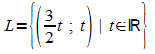 
.
Aus der Bedingung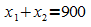 
ergibt sich
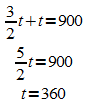
Es gibt also eine Verteilung, die "stabil" ist, d.h. sich nicht mehr verändert:
|
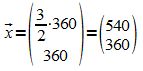
Definition: Wenn A die Matrix
eines Austauschprozesses ist, dann heißt jeder Vektor |
2. Als zweites Beispiel wird der Prozess aus Aufgabe 1 in
Abschnitt 4.1 betrachtet:
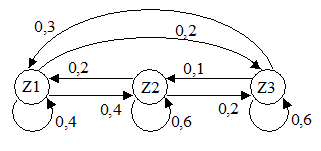
Die Anfangsverteilung auf die drei Zustände Z1, Z2 und Z3 sei
.
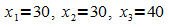Die Übergangsmatrix des Prozesses ist
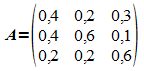
Sie enthält nur nicht-negative Elemente. Die Summe der Elemente beträgt
in Spalte 1: 0,4 + 0,4 + 0,2 = 1
in Spalte 2: 0,2 + 0,6 + 0,2 = 1
in Spalte 3: 0,3 + 0,1 + 0,6 = 1
Der Prozess ist also ein Austauschprozess.
Für stationäre Verteilungen des Prozesses gilt
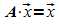
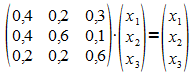
Dies führt auf folgendes homogenes lineares Gleichungssystem:
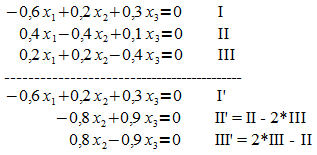
Die beiden Gleichungen II' und III' sind identisch. Das Gleichungssystem besitzt daher eine nicht-triviale Lösung. Aus Gl. II' ergibt sich:
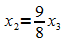
Einsetzen in Gl. I' und umstellen nach x1 führt auf
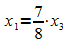
Die Lösungsmenge des Gleichungssystems ist somit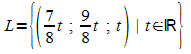 
.
Aus der Bedingung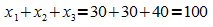 
folgt
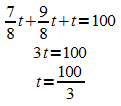
Die gesuchte stationäre Verteilung des Prozesses lautet damit
mit nicht-negativen Elementen 
beschrieben wird, bei der in allen Spalten die
Summe der Elemente gleich 1 ist, wird ein Austauschprozess genannt.
eine stationäre Verteilung des
Prozesses (oder auch ein Fixvektor von A).