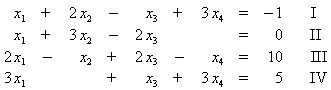
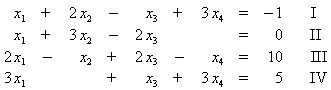
kann mit Matrizen und Vektoren notiert werden. Die linke Seite kann als ein Matrix-Vektor-Produkt geschrieben werden:
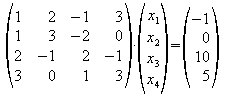
Die hier auftretende Matrix enthält die Koeffizienten des Gleichungssystems und wird deswegen als Koeffizientenmatrix bezeichnet. Die Koeffizientenmatrix wird mit einem Spaltenvektor multipliziert, der die Variablen enthält. Die rechte Seite des Gleichungssystems wird in einem weiteren Spaltenvektor zusammengefasst.
Allgemein: Ein lineares Gleichungssystem
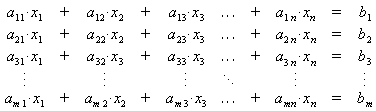
lässt sich in Matrix-Vektor-Schreibweise notieren:
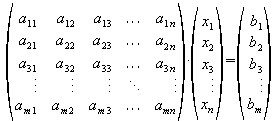 .
.
Ganz kurz:
![]() .
.
Für die praktische Berechnung kann folgendes Schema mit der erweiterten Koeffizientenmatrix verwendet werden.
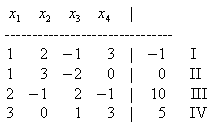
Hier werden jetzt – wie oben bei den vollständig ausgeschriebenen Gleichungssystemen – Zeilenumformungen vorgenommen, um die Koeffizientenmatrix auf Stufenform zu bringen.

Schrittweises Auflösen:
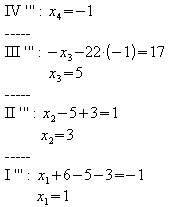
![]()
Übungen
1.
| a) 2x1 – 3x2
– 5x3 = 1
2x2 + x3 = 0 3x3 = 6 |
b) 3x1 + 4x2
+ 6x3 = -5
17x2 + 24x3 = -16 2x3 = -7 |
c) 3x1 + 8x2
– 3x3 = 5
4x2 + x3 = 1 5x3 = -10 |
| d) x1 + 3x2
+ x3 = 19
-x1 + x2 – x3 = -7 2x1 + 2x2 + x3 = 18 |
e) 2x1 – x2
+ 3x3 = 0
-x1 + 2x2 – 5x3 = 7 3x1 – 4x2 + 7x3 = -6 |
f) 6x1 – 5x2
+ 2x3 = 8
-3x1 + 10x2 + 3x3 = -11 x2 + 4x3 = 0 |
| g) 4x1 – 3x2
+ 6x3 = 9
2x1 - x3 = 5 4x1 = -2 |
h) 4x1 - x2
+ 3x3 = 2
x1 + 3x2 = 5 4x2 = 8 |
i) 3x1 + 4x2
+ 6x3 = -5
2x1 – 3x2 – 4x3 = 2 x1 + 2x2 – 4x3 = 22 |
2.
| a) x1 + 2x2
– 4x3 = 3
x1 + x3 = 0 3x2 – 2x3 = -1 |
b) x1 + x2
+ x3 = 0
2x1 + 4x2 + 3x3 = 0 4x2 + 4x3 = 0 |
c) 2x1 – 3x2
+ 4x3 = 1
3x1 + x2 – 5x3 = 7 7x1 – 5x2 + 3x3 = 9 |
| d) x1 – x2
= 1
x1 – x2 + x3 = 2 x1 – x2 – x3 = 0 |
e) 2x2 – 6x3
= 1
x1 + x2 = 4 4x2 = 10 |
f) 8x1 = 16
5x2 – 3x3 = 9 4x1 + x2 = 0 |
| g) 2x1 – 4x2
+ x3 = 0
x1 + 3x2 + 5x3 = 0 4x1 - x2 - x3 = 0 |
h) 2x1 – 4x2
+ x3 = 0
x1 + 3x2 + 5x3 = 0 3x1 - x2 + 6x3 = 0 |
i) 2x1 – 4x2
+ x3 = 0
4x1 – 8x2 + 2x3 = 0 -8x1 + 16x2 – 4x3 = 0 |
Lösungen
1. a) (x1;x2;x3) = (4; –1; 2)
b) (x1;x2;x3) = (0; 4; –7/2)
c) (x1;x2;x3) = (–7/3; 3/4; –2)
d) (x1;x2;x3) = (2; 3; 8)
e) (x1;x2;x3) = (2,9; 0,7; –1,7)
f) (x1;x2;x3) = (9/26; -28/26; 7/26)
g) (x1;x2;x3) = (–0,5; –47/3; –6)
h) (x1;x2;x3) = (–1; 2; 8/3)
i) (x1;x2;x3)
=
(0; 4; –3,5)
2. a) (x1;x2;x3) = (1: –1; –1)
b) (x1;x2;x3) = (0; 0; 0)
c) L = { (x1;x2;x3) | x1 = 2 + x3; x2 = 1 + 2x3; x3ÎR }
d) L = { (x1;x2;x3) | x1 = 1 + x2; x2ÎR; x3 = 1}
e) (x1;x2;x3) = (3/2; 5/2; 2/3)
f) (x1;x2;x3) = (2; –8; –49/3)
g) (x1;x2;x3) = (0; 0; 0)
h) L = { (x1;x2;x3) | x1 = (–23/10)x3; x2 = (–9/10)x3; x3ÎR }
i) L = { (x1;x2;x3) | x1 = 2x2 – (1/2)x3; x2ÎR ; x3ÎR }