
|
Kasten
Baustein |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eine Firma A bestellt folgende Baukästen: 1 Basis, 1 Ausbau 1, 5 Ausbau 2, 8 Luxus. Wie viele Bausteine der einzelnen Typen muss die Produktionsfirma dafür herstellen?
Die dazu nötige Rechnung ist einfach: die Bestellmengen der einzelnen Baukästen sind jeweils mit der zu dem Baukasten gehörigen Anzahl an Bausteintypen zu multiplizieren.

Unter Verwendung von Matrizen und Vektoren lässt
sich die Rechnung kürzer schreiben:
|
|
 |
|
|
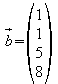 |
|
|
 |
|
|
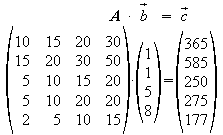 |
Ein Element des Produktionsvektors ergibt sich also, indem die Elemente der entsprechenden Zeile der Modellmatrix mit den Elementen des Bestellvektors multipliziert und die einzelnen Produkte addiert werden. Diese Rechenoperation wird als Skalarprodukt des Zeilenvektors der Matrix mit dem Spaltenvektor bezeichnet.

| Definition:
Ist
|
Übungen
Berechnen Sie die folgenden Produkte.
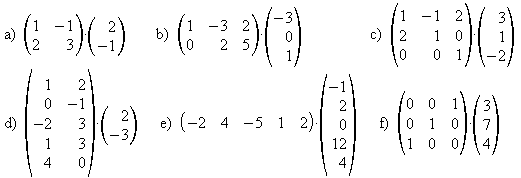
|
Firma
Baukasten |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sollen wie oben die Berechnungen für alle 6 Firmen durchgeführt werden, so könnte eine ähnliche Rechnung fünfmal wiederholt werden. Die Rechnung lässt sich aber auch in einem Schritt zusammenfassen:
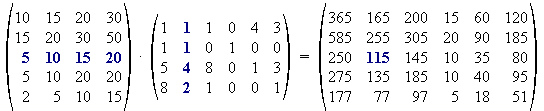 .
.
Hier wurden die Bestellungen der einzelnen Firmen
als Spaltenvektoren geschrieben und zu einer Auftragsmatrix zusammengefasst.
Jede Spalte dieser Auftragsmatrix wurde wie ein Vektor mit der Modellmatrix
multipliziert. Die Spaltenvektoren der Ergebnisse dieser Multiplikationen
wurden wieder zu einer Matrix zusammengefasst. Insgesamt wurde also die
Modellmatrix mit der Auftragsmatrix verknüpft, und das Ergebnis ist
die Produktionsmatrix.
| Definition:
Ist
|
Zu beachten ist also: Man kann zu zwei Matrizen A und B nur dann das Produkt A.B bilden, wenn die Anzahl der Spalten des ersten Faktors A mit der Anzahl der Zeilen des zweiten Faktors B übereinstimmt.
Übungen
1. Berechnen Sie das Matrizenprodukt A.B
der Matrizen.
Prüfen Sie, ob auch das Produkt B.A
gebildet
werden kann. Wenn ja: berechnen Sie auch B.A und
vergleichen Sie mit dem Produkt A.B.

2. Prüfen Sie, ob der angegebene Matrizenterm
sich bilden lässt.
Wenn ja: berechnen Sie das Produkt.
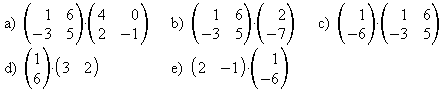
3. a) Berechnen Sie das Matrizenprodukt 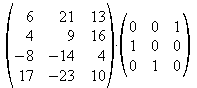 .
Was fällt auf?
.
Was fällt auf?
b) Berechnen Sie das Matrizenprodukt 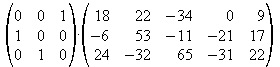 .
Was fällt auf?
.
Was fällt auf?
4. Gegeben ist die quadratische Matrix ![]() .
Berechnen Sie
.
Berechnen Sie
![]()
5. Die Firma „Quadrupedia“ stellt Ergänzungsfutter
in Tablettenform für Tiere her, das Mangelerscheinungen vorbeugen
soll. Das Produktangebot ist differenziert nach Hunden, Katzen und Mäusen.
Die Wirkstoffe A, B, C und D sind in den drei Sorten in unterschiedlichen
Mengen kombiniert und müssen zu den angegebenen Preisen bezogen werden.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wirkstoff A: 12,50 Euro pro kg;
Wirkstoff B: 27,50 Euro pro kg
Wirkstoff C: 31,20 Euro pro kg
Wirkstoff D: 5,00 Euro pro kg
Berechnen Sie die Stückkosten des Herstellers für jedes Produkt.
6. a) Geben Sie zwei ![]() an, die jeweils von der Nullmatrix
an, die jeweils von der Nullmatrix  verschieden sind und für die gilt A.B =
0.
verschieden sind und für die gilt A.B =
0.
b) Geben Sie eine von der Nullmatrix verschiedene ![]() an, für die gilt A.A = 0.
an, für die gilt A.A = 0.
(1) Assoziativgesetz:
a) ![]()
b) ![]()
(2) Kommutativgesetz:
gilt nicht. Im Allgemeinen ist ![]() .
.
(3) neutrales Element:
Bei der Multiplikation reeller Zahlen ist die
1 das sog. neutrale Element:![]() .
.
Bei der Multiplikation von Matrizen sind dies
die Einheitsmatrizen. Eine Einheitsmatrix ist eine quadratische ![]()
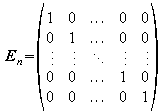 .
.
Für jede ![]() und für jede
und für jede ![]() gilt:
gilt:
![]() .
.
(4) inverses Element:
Bei der Multiplikation reeller Zahlen gibt es
zu jeder Zahl ![]() ein inverses Element:
ein inverses Element: ![]() .
.
Bei der Multiplikation von Matrizen kann es höchstens
für quadratische Matrizen inverse Matrizen geben (warum?). Zwei quadratische ![]() heißen invers zueinander, wenn gilt
heißen invers zueinander, wenn gilt ![]() .
Für die zu einer Matrix A inverse Matrix schreibt man
auch A–1:
.
Für die zu einer Matrix A inverse Matrix schreibt man
auch A–1:
![]() .
.
(5) Distributivgesetze:
Falls sich die Terme überhaupt bilden lassen gilt:
![]()
Übungen
1. Bestätigen Sie für die folgenden
3 Matrizen das Assoziativgesetz ![]() .
.
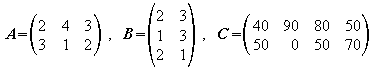
2. Berechnen Sie A.B und B.A und vergleichen Sie.
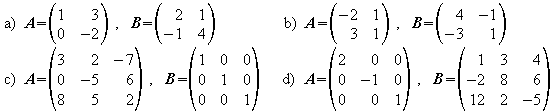
3. Zeigen Sie, dass die Matrizen A und B zueinander invers sind.
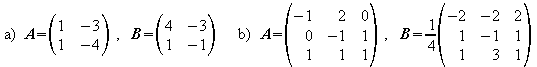
4. Es ist ![]() .
Bestimmen Sie alle Matrizen B mit A.B
= B.A. Setzen Sie dazu
.
Bestimmen Sie alle Matrizen B mit A.B
= B.A. Setzen Sie dazu ![]() und bestimmen Sie die Elemente von B aus der Gleichung
A.B
= B.A.
und bestimmen Sie die Elemente von B aus der Gleichung
A.B
= B.A.
5. Es ist ![]() .
Bestimmen Sie B so, dass A und B
invers zueinander sind. Setzen Sie dazu
.
Bestimmen Sie B so, dass A und B
invers zueinander sind. Setzen Sie dazu ![]() und bestimmen Sie die Elemente von B aus der Gleichung
A.B
= E2.
und bestimmen Sie die Elemente von B aus der Gleichung
A.B
= E2.
6. Es ist ![]() .
Zeigen Sie: Wenn es zu A eine inverse Matrix A–1
gibt, dann ist
.
Zeigen Sie: Wenn es zu A eine inverse Matrix A–1
gibt, dann ist ![]() .
.