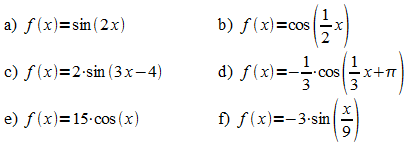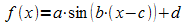
In Anwendungen treten meistens allgemeine Sinusfunktionen auf, deren Graphen durch Veränderungen des Graphen von sin(x) entstehen:
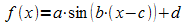
Beispiel:
Im
folgenden interaktiven Java- Applet können Sie entsprechend zum
Beispiel verschiedene
Werte für die Parameter a, b, c und d
einstellen und die Auswirkungen untersuchen.
Ergebnis:
Der
Vergleich von 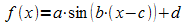 und
und 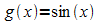 zeigt:
zeigt:
a bewirkt
d bewirkt
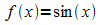 und
und 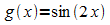 dargestellt.
dargestellt.
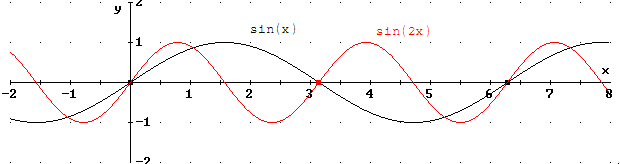
Die
Sinusfunktion hat die Periode 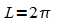 ,
das bedeutet, zwischen x = 0 und
,
das bedeutet, zwischen x = 0 und 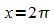 nimmt die Sinusfunktion alle Werte ihrer Wertemenge
nimmt die Sinusfunktion alle Werte ihrer Wertemenge 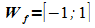 an. Der Abbildung ist zu entnehmen, dass die Funktion
an. Der Abbildung ist zu entnehmen, dass die Funktion 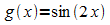 offensichtlich die Periode
offensichtlich die Periode 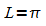 besitzt. Ohne Bezug auf den Graphen nehmen zu müssen, lässt
sich dies auch so begründen:
besitzt. Ohne Bezug auf den Graphen nehmen zu müssen, lässt
sich dies auch so begründen:
Das
Argument von g(x) = sin(2 x) muss die Werte von 0 bis 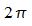 durchlaufen, dann hat g alle Werte der Wertemenge [-1; 1]
einmal angenommen, d.h. es ist eine Periode von g durchlaufen
worden. Es muss also gelten:
durchlaufen, dann hat g alle Werte der Wertemenge [-1; 1]
einmal angenommen, d.h. es ist eine Periode von g durchlaufen
worden. Es muss also gelten:
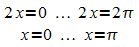
Die
Funktion g mit g(x) = sin(2 x) besitzt also die
Periode 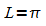 .
.
Entsprechend
werden verglichen: 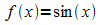 und
und 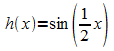 .
.
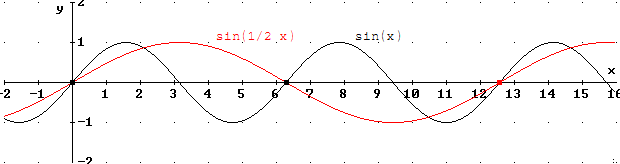
Das
Argument von 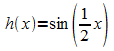 muss die Werte von 0 bis
muss die Werte von 0 bis 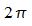 durchlaufen, dann hat h alle Werte der Wertemenge [-1; 1]
einmal angenommen, d.h. es ist eine Periode von h durchlaufen
worden. Es muss also gelten:
durchlaufen, dann hat h alle Werte der Wertemenge [-1; 1]
einmal angenommen, d.h. es ist eine Periode von h durchlaufen
worden. Es muss also gelten:
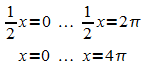
Die
Funktion h mit 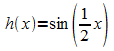 besitzt also die Periode
besitzt also die Periode 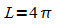 .
.
Allgemein:
In 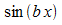 muss gelten:
muss gelten:
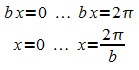
Die
Periode ist also 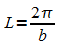 .
Bei gegebenem Parameter b kann damit die Periodenlänge L
berechnet werden. Ist umgekehrt die Periodenlänge gegeben (etwa
aus einem gegebenen Graphen einer allgemeinen Sinusfunktion
abgelesen), dann lässt sich der Parameter b bestimmen:
.
Bei gegebenem Parameter b kann damit die Periodenlänge L
berechnet werden. Ist umgekehrt die Periodenlänge gegeben (etwa
aus einem gegebenen Graphen einer allgemeinen Sinusfunktion
abgelesen), dann lässt sich der Parameter b bestimmen: 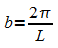 .
.
Angemerkt
sei noch, dass alle genannten Zusammenhänge ebenso für die
allgemeine Kosinusfunktion 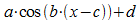 gelten. Bei der allgemeinen Tangensfunktion
gelten. Bei der allgemeinen Tangensfunktion 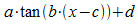 ist jedoch zu bedenken, dass die Periode von tan(x) nur
ist jedoch zu bedenken, dass die Periode von tan(x) nur ![]() ist; daher ist der Zusammenhang von Parameter b und
Periodenlänge L :
ist; daher ist der Zusammenhang von Parameter b und
Periodenlänge L : 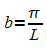 .
.
Übungen
1. Wo liegen die Nullstellen der trigonometrischen Funktionen sin, cos und tan?
2. Bestimmen Sie die Nullstellen und Perioden von
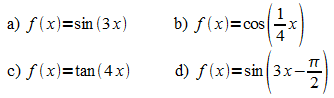
3. Die
Abbildung zeigt den Graphen einer allgemeinen Sinusfunktion 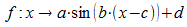 .
.
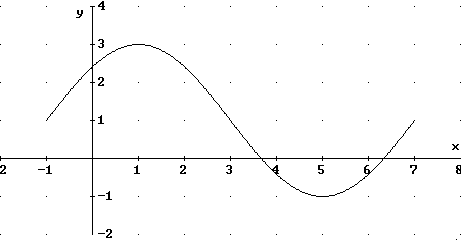
Bestimmen Sie die Werte der Parmeter a, b, c und d.
4. Unter der Globalstrahlung G versteht man die aus allen Raumrichtungen ankommende direkte und indirekte Sonnenstrahlung. Für Hamburg haben langjährige Messungen folgende Mittelwerte ergeben.
|
Monat |
G in Wh/m² |
|
Januar |
521 |
|
Februar |
1132 |
|
März |
2231 |
|
April |
3553 |
|
Mai |
4688 |
|
Juni |
5437 |
|
Juli |
4820 |
|
August |
4340 |
|
September |
2786 |
|
Oktober |
1489 |
|
November |
671 |
|
Dezember |
401 |
Für die Berechnung von Anlagen, die Solarenergie in elektrische Energie umwandeln, wird eine Funktion benötigt, welche diesen Verlauf (näherungsweise) beschreibt.
a) Stellen Sie die Messpunkte in einem Diagramm dar, wobei der Monat Januar mit x = 0, der Februar mit x = 1, ... der Dezember mit x = 11 und für eine volle Periode noch einmal der Januar mit x = 12 bezeichnet wird.
b) Es scheint im wesentlichen eine allgemeine Sinusfunktion vorzuliegen. Bestimmen Sie deren Parameter a, b, c und d.
5. Bestimmen Sie zu f jeweils die Periode L, die erste Ableitung f ' sowie eine Stammfunktion F.