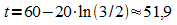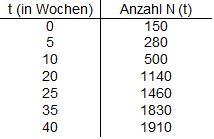
1. Wenn eine Anzahl von Kaninchen auf eine Insel gebracht wird, auf der sie sich ungestört ausbreiten können, dann vermehren sie sich anfangs sehr schnell. Durch die Zunahme der Anzahl sinkt aber das Nahrungsangebot, da die Kaninchen schneller die Vegetation abfressen als diese nachwachsen kann. Das hat zur Folge, dass die Vermehrungsrate der Kaninchen absinkt. Die Insel bietet nur einer bestimmten Anzahl S (Sättigungsgrenze) von Kaninchen Lebensraum. Beispiel:

Anfangs verläuft die Vermehrung der Kaninchen näherungsweise exponentiell. Bei Annäherung an die Sättigungsgrenze kann die Entwicklung des Bestandes näherungsweise als begrenztes Wachstum beschrieben werden.

Bei exponentiellem Wachstum einer Größe, die durch eine differenzierbare Funktion f(t) beschrieben wird, gilt: Die momentane Änderungsrate (Wachstumsgeschwindigkeit) f '(t) ist proportional zum momentanen Bestand:
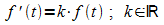
Das begrenzte Wachstum (mit Sättigungsgrenze S) ist dadurch gekennzeichnet, dass die momentane Änderungsrate (Wachstumsgeschwindigkeit) f '(t) proportional zum aktuellen Sättigungsdefizit ist:
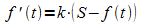
Für ein Wachstum, wie es im Beispiel der Kaninchenpopulation auftritt, liegt daher folgender Ansatz nahe:
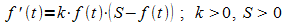
Ein solches Wachstum wird allgemein als logistisches Wachstum bezeichnet. Die Lösungen dieser Differentialgleichung heißen logistische Funktionen. Eine Form einer logistischen Funktion ist:
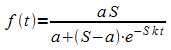
Dabei ist 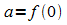 der Anfangswert mit
der Anfangswert mit 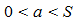 und
und 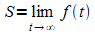 die Sättigungsgrenze.
die Sättigungsgrenze.
Herleitung der Lösung:
Die Grundidee zur Lösung der Differentialgleichung 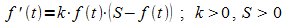 beruht auf folgendem Zusammenhang:
beruht auf folgendem Zusammenhang:
Eine Stammfunktion von 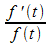 ist
ist 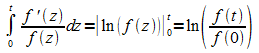 .
.
Um diesen Zusammenhang ausnutzen zu können, wird die Differentialgleichung zunächst umgeschrieben:
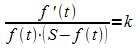
Der Bruch kann zerlegt werden:
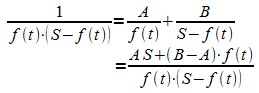
Damit der Zähler für alle zulässigen Werte von t
den Wert 1 ergibt, muss gelten:
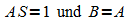
Also:
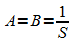
Wird diese Zerlegung auf die umgeschriebene Form der Differentialgleichung angewendet, so folgt:
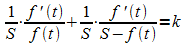
Integration führt nun auf
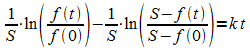
Unter Ausnutzen von 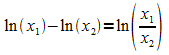 lässt sich die linke Seite umschreiben:
lässt sich die linke Seite umschreiben:
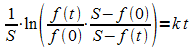
Entlogarithmieren:
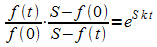
Auflösen nach f(t):
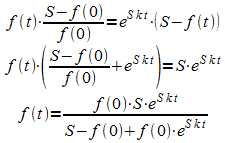
Erweitern mit 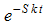 ergibt schließlich die oben genannte Form der logistischen
Funktion:
ergibt schließlich die oben genannte Form der logistischen
Funktion:
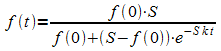
2. Bestimmen einer logistischen Funktion
In Anwendungen liegen häufig Daten wie in obigem einführenden
Beispiel der Kaninchenvermehrung vor. Wenn der Zusammenhang durch
eine logistische Funktion modelliert werden kann, dann sind die
Parameter a, S und k zu bestimmen. Das Vorgehen
soll am Beispiel der Kaninchenvermehrung erläutert werden. Hier
ist 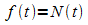 .
.
Falls die Sättigungsgrenze S nicht aus der Problemstellung hervorgeht, wird zunächst ein Schätzwert für S gewählt - im Beispiel bietet sich S = 2000 an.
Dann wird der Kehrwert des Funktionsterms gebildet:
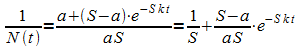
Dieser Kehrwert wird weiter umgeformt:
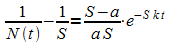
Logarithmieren führt auf:
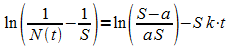
Das entspricht einer Geradengleichung
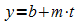
mit: 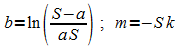
Die Parameter b und m können bestimmt werden, indem man die Daten in einem t-y-Diagramm darstellt und eine Ausgleichsgerade anpasst:
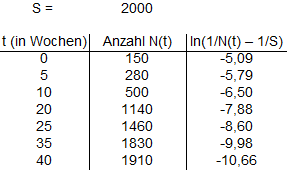
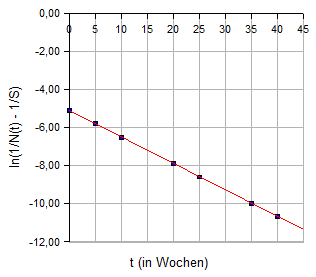
Die Gleichung der Ausgleichsgeraden lautet im vorliegenden Fall
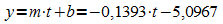
Mit dem (geschätzten) Wert für S können dann die Wachstumskonstante k und der Anfangswert a bestimmt werden:
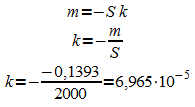
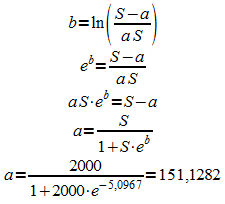
Die gesuchte logistische Funktion lautet somit
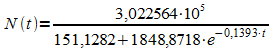
Das folgende Diagramm zeigt, dass durch diese Funktion die gegebenen Datenpunkte gut erfasst werden.
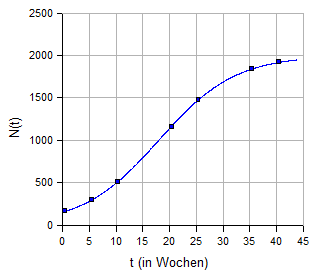
3. Beispiel 1: Höhenwachstum eines Strauches
Das Höhenwachstum eines Strauches wird in guter Näherung
durch eine logistische Funktion beschrieben: 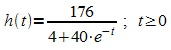 .
Dabei
ist t die Zeit in Jahren und h(t) die Höhe
in Dezimetern.
.
Dabei
ist t die Zeit in Jahren und h(t) die Höhe
in Dezimetern.
Die Parameter a, S und k ergeben sich wie folgt:
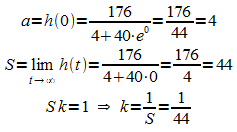
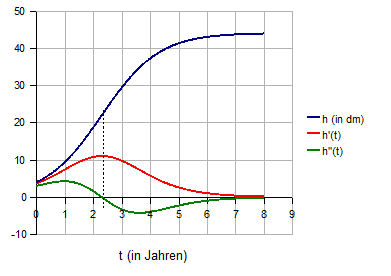
Graph von h:
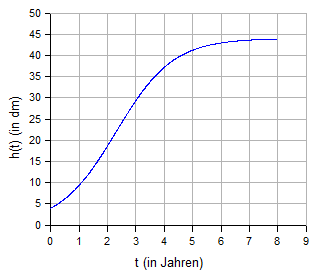
Der Verlauf des Graphen lässt vermuten, dass die Änderungsrate von h, also die Wachstumsgeschwindigkeit, einen maximalen Wert besitzt. Der zugehörige Zeitpunkt tW ist dann eine Wendestelle von h. Die Ermittlung dieser Wendestelle kann in gewohnter Weise erfolgen. Unter Verwendung von Quotienten- und Kettenregel ergibt sich:
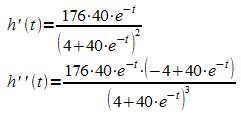
h'' besitzt eine Nullstelle, wenn der Klammerterm im Zähler Null wird:
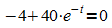
Das ist der Fall für 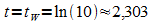 .
h'' wechselt an dieser Stelle das Vorzeichen von + nach -.
Somit ist tW eine LR-Wendestelle und damit
eine Maximalstelle der Wachstumsgeschwindigkeit h'. Der
Funktionswert von h beträgt an dieser Stelle
.
h'' wechselt an dieser Stelle das Vorzeichen von + nach -.
Somit ist tW eine LR-Wendestelle und damit
eine Maximalstelle der Wachstumsgeschwindigkeit h'. Der
Funktionswert von h beträgt an dieser Stelle
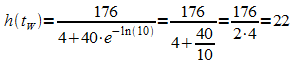
4. Beispiel 2: Energiebedarf
In einem Planungsmodell zur Energieversorgung eines Landes wird die momentane Änderungsrate des Energiebedarfes mit folgender logistischer Funktion nachgebildet:
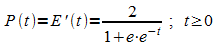
Dabei ist t die Zeit in Jahren ab Anfang des Planungsjahres
und P(t) wird in 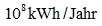 berechnet.
berechnet.
Anfangswert und Sättigungsgrenze:
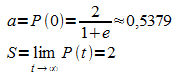
Graph:
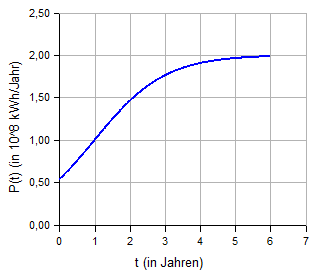
Wendestelle:
Mit Quotienten- und Kettenregel ergeben sich die Ableitungen:
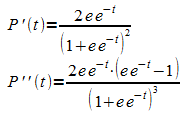
Die zweite Ableitung hat eine Nullstelle mit Vorzeichenwechsel bei
t = tW = 1. Der Funktionswert an
dieser Wendestelle ist 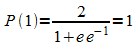 .
.
Gesamtenergiebedarf in einem bestimmten Zeitraum:
Der Gesamtenergiebedarf ergibt sich durch Integration über die momentane Änderungsrate:
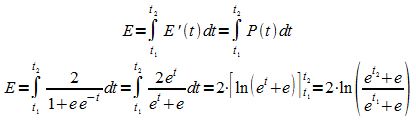
Für den Zeitraum 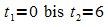 ergibt sich E = 9,387. Der Energiebedarf beträgt somit
ergibt sich E = 9,387. Der Energiebedarf beträgt somit 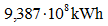 .
.
Übungen
1. Eine Bakterienkultur wächst logistisch mit k = 0,02 und bedeckt eine Fläche A(t). Dabei ist t die Zeit ab Beobachtungsbeginn gemessen in Stunden. Nach 10 Stunden beträgt die bedeckte Fläche 8 cm2. Die Sättigungsgrenze ist S = 20 cm2.
a) Stellen Sie eine geeignete logistische Funktion zur Beschreibung des Flächenwachstums auf.
b) Bestimmen Sie den Zeitpunkt t1, zu dem die bedeckte Fläche 0,1 cm2 betrug, und den Zeitpunkt t2, zu dem die Fläche 90% des Sättigungswerts erreicht.
c) Zeichnen Sie die Graphen von A(t) und der
momentanen Änderungsrate (Wachstumsgeschwindigkeit).
2. Der Durchmesser einer Fichte (gemessen in 1,3 m Höhe)
wird näherungsweise durch die Funktion 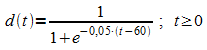 beschrieben (d in m, t in Jahren)
beschrieben (d in m, t in Jahren)
a) Bestimmen Sie den Anfangswert a = d(0) und die
Sättigungsgrenze 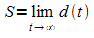 .
.
b) Zeigen Sie, dass d(t) der Differentialgleichung 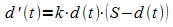 genügt, also eine logistische Funktion ist.
genügt, also eine logistische Funktion ist.
c) Bestimmen Sie den Wendepunkt von d.
d) Zeichnen Sie den Graphen von d im Bereich 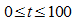 .
.
e) Ermitteln Sie das Alter einer Fichte mit 0,4 m Durchmesser.
Lösungen
1. a) 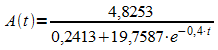
b) 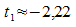 ,
also
2,22 Stunden vor Beobachtungsbeginn;
,
also
2,22 Stunden vor Beobachtungsbeginn; 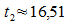
c) 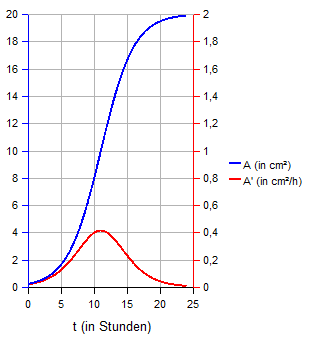
2. a) 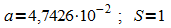
b) (nachrechnen; k = 0,05)
c) 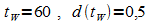
d) 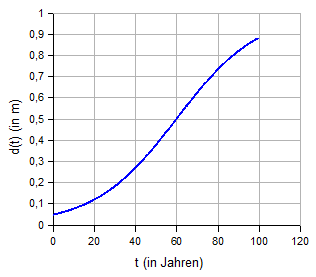
e)