9.2 Begrenztes Wachstum

Darin ist

• t die Zeit,
• N(t) die Anzahl der verkauften Geräte,
• S der Sättigungswert, d.h. die maximale Anzahl des Artikels, die am Markt abgesetzt werden kann.
• S - N(t) ist dann die Anzahl der potentiellen Kunden, die den Artikel noch nicht erworben haben.

Dann lautet die Wachstumsfunktion des begrenzten Wachstums

Der Anfangswert N₀ = N(0) kann von Null verschieden sein:

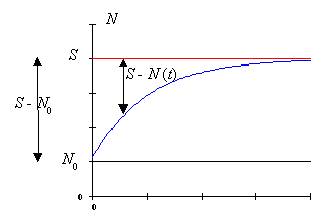
In diesem Fall folgt aus dem Ansatz  die Wachstumsfunktion

Beispiel 1: Marktsättigung

Eine Firma will in einer Stadt ein neues Küchengerät, das noch in keinem Haushalt vorhanden ist, einführen. Es wird zunächst in einem Stadtteil mit 2000 Haushalten ein Testverkauf begonnen. Nach einer Woche sind 363 Geräte verkauft.

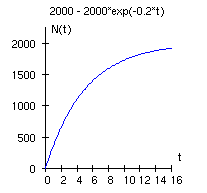
a) Der Verkauf der Geräte soll als begrenztes Wachstum modelliert werden. Da zu Beginn des Verkaufs in den Haushalten noch keine Geräte vorhanden sind, ist N₀ = 0. Der Sättigungswert ist gleich der Anzahl der Haushalte: S = 2000. Für die Anzahl der abgesetzten Geräte wird die Funktion  angenommen. Dabei ist die t die Zeit in Wochen nach Verkaufsbeginn. Die Wachstumskonstante ergibt sich aus der Anzahl der nach t = 1 Woche verkauften Geräte:

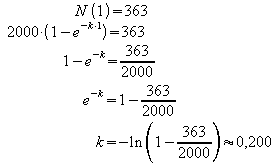
b) Nach welcher Zeit t_H haben nach diesem Modell die Hälfte aller Haushalte das Gerät gekauft?

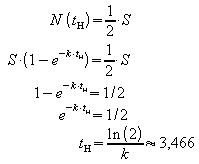
Es dauert also etwa 3,5 Wochen, bis die Hälfte der Haushalte das Gerät erworben hat.

c) Wann sind voraussichtlich 1900 Geräte verkauft?

Entsprechend zu b) ist anzusetzen:

Auflösen nach t (wie in b)) ergibt:- also etwa 15 Wochen.

d) Die momentane Wachstumsgeschwindigkeit N'(t) ist proportional zum aktuellen Sättigungsdefizit:

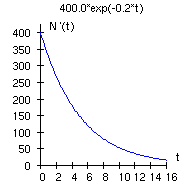
e) Für das Integral der Wachstumsfunktion ergibt sich:

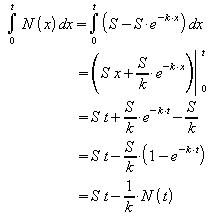
Beispiel 2: radioaktive Zerfallskette

Eine radioaktive Substanz A zerfalle mit der Zerfallskonstanten k_A in eine Substanz B. Die Menge von B wächst dann exponentiell an. Dieses Wachstum ist aber begrenzt: Hat sich die Menge von A durch Zerfall in die Substanz B umgewandelt, kommt es zu keinem weiteren Zuwachs von B.

Bei radioaktiven Zerfällen ist es oft so, dass die aus dem Zerfall von A entstandene Substanz B selbst auch radioaktiv ist, und erst aus dem Zerfall dieser Substanz stabile Endprodukte entstehen. Eine solche Zerfallskette kann mit den beiden folgenden Gleichungen modeliert werden:

Abnahme von A durch Zerfall:

Zunahme von B durch Umwandlung von A in B und gleichzeitiger Zerfall von B:

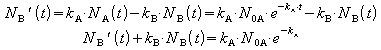
Diese Differentialgleichung für N_B(t) hat die Lösung

a) Eine radioaktive Substanz A hat zur Zeit t = 0 den Anfangswert von N_0A = 10 Mengeneinheiten. Sie zerfällt mit der Halbwertszeit t_HA = 1 Stunde in eine Substanz B. Die Substanz B ist ebenfalls radioaktiv und zerfällt mit der Halbwertszeit t_HB = 5 Stunden. Wie lautet die Wachstumsfunktion für N_B(t)?

Aus den Halbwertszeiten ergeben sich die Zerfallskonstanten:

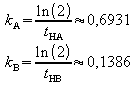
Damit folgt:

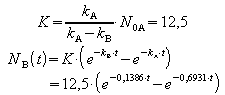
b) Zu welcher Zeit t_m ist die Menge der Substanz maximal? Wie groß ist dieser Maximalwert?

Benötigt werden die erste und die zweite Ableitung von N_B(t):

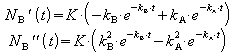
notwendige Bedingung für lokale Extrema: .

Dies ist der Fall, wenn

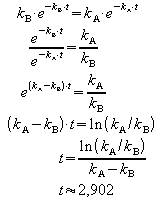
Überprüfung der hinreichenden Bedingung für lokale Extrema: 

Für ist

Also ist

lokale Maximalstelle. Der Maximalwert der Menge der Substanz B beträgt daher

c) Die Menge der Substanz B nimmt von 0 beginnend zunächst zu, erreicht bei t_m ihren Maximalwert und nimmt dann wieder ab. Da sich N_B(t) asymptotisch dem Wert 0 nähert ist zu erwarten, dass der Graph von N_B einen Wendepunkt besitzt. Dieser soll bestimmt werden.

Notwendige Bedingung für Wendestellen: 

Dies ist der Fall für

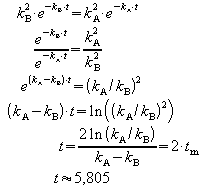
Hinreichende Bedingung für Wendestellen: 

Die dritte Ableitung lautet:

Für ist

Also ist

Wendestelle mit Steigungsminimum (RL-Wendestelle). Der Wert von N_B beträgt hier

Der gesuchte Wendepunkt ist also W(5,805 | 5,367).

d) Die folgenden Abbildungen zeigen die Graphen von N_B(t) und N_B'(t).

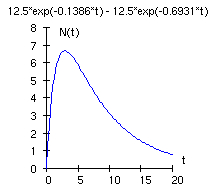
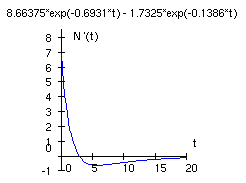
e) Welche Bedeutung hat?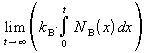

Das Integral von N_B ist

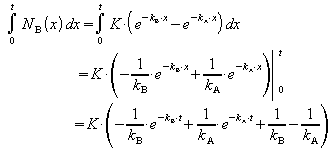
Unter Berücksichtigung von

ergibt sich daraus:

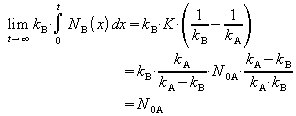
Dies ist die Anfangsmenge der Substanz A.

Übungen

1. Ein Kondensator der Kapazität  wird über einen Widerstand  an eine Spannungsquelle mit der Spannung  angeschlossen. Die Spannung am Kondensator U (t) wächst dann gemäß der folgenden Beziehung:

Dabei wird die Spannung in Volt und die Zeit in Sekunden gemessen.

a) Nach welcher Zeit t_H ist die Spannung am Kondensator auf die Hälfte ihres Endwertes angestiegen?

b) Bestimmen Sie die Gleichung der Tangente an den Graphen von U zur Zeit t = t_H.

2.Gegeben ist die Funktion g durch 

a) Bestimmen Sie die Null- und Extremstellen von g.

b) Wie verhält sich g für?
Zeichnen Sie den Graphen von g in ein Koordinatensystem ein.

c) Bestimmen Sie den Flächeninhalt der Fläche, die von dem Graphen von g , der x-Achse und der
y-Achse begrenzt wird.

d) Beim radioaktiven Zerfall einer Substanz S₁ beschreibt h₁(t) die Masse der noch nicht zerfallenen Substanz zum Zeitpunkt t.(h₁(t)in mgund t in Stunden nach Beobachtungsbeginn).
Dabei gilt: .
Wie groß ist die Halbwertszeit dieses Zerfalles, d.h. die Zeit, nach der nur noch die Hälfte der
ursprünglichen Substanz vorhanden ist?
Welche Masse ist nach 6 Stunden bereits zerfallen?

e) Eine zweite radioaktive Substanz S₂ entsteht erst als Zerfallsprodukt einer anderen Substanz. Für
die Masse h₂(t)der noch nicht zerfallenen Substanz S₂ gilt:

.

Bestimmen Sie den Bestand für t = 0 .
Zu welchem Zeitpunkt wird die größte Masse gemessen und wie groß ist sie?
In welchem Zusammenhang stehen die Funktionen h₂ und g ?

Welche Bedeutung hat das Integral ?

(Beachten Sie Ihren in Aufgabenteil c) berechneten Flächeninhalt).

3. Die Konzentration von Drogen im Blutplasma lässt sich in Abhängigkeit von der Zeit t (gemessen in Stunden) modellhaft darstellen durch

Dabei sind a, b und c positive Konstanten, die vom Wirkstoff, seiner Menge und der Verabreichungsform abhängen. Injiziert man einer Person von 70 kg Körpergewicht eine Dosis von 140 Mikrogramm LSD, so gibt die folgende Funktion die Konzentration in Nanogramm pro Kilogramm Körpergewicht an:

a) Zu welcher Zeit t_m ist die Konzentration f maximal?

b) Zeigen Sie, dass der Graph von f einen Wendepunkt besitzt und berechnen Sie diesen.

c) Zeichnen Sie die Graphen von f und f '. Erläutern Sie den Verlauf des Graphen von f.

4. Durch den Treibhauseffekt führt eine Erhöhung des CO₂-Anteils der Atmosphäre zu einer Erhöhung der Lufttemperatur. Modellrechnungen ergeben für die Temperaturerhöhung T (in Grad) in Abhängigkeit von der CO₂-Konzentration x (in ppm) die Funktion

Bestimmen Sie für die angegebene Definitionsmenge D_T die Wertemenge und das Monotonieverhalten von T.

Zeichnen Sie den Graphen von T im angegebenen Intervall.

Was ergibt sich für ?