9. Wachstumsvorgänge

9.1 Exponentielles Wachstum

• Verzinsung eines Kapitals;
• Abnahme der unzerfallenen Atome beim radioaktiven Zerfall;
• Wachstum eines Holzbestandes, einer Bakterienkultur, einer Population, ...
• Verhalten der Stromstärke beim Ein- und Ausschalten eines Gleichstroms in einem Stromkreis mit Widerstand und Kapazität oder Induktivität.

Zum Zeitpunkt t sei ein Anfangsbestand von N (t) Bakterien vorhanden. Zu einem späteren Zeitpunkt  sind dann durch Vermehrung  Bakterien vorhanden. Wenn äußere Einflüsse auf das Wachstum der Bakterien ausgeschlossen sind, wird in Versuchen beobachtet:

• je mehr Bakterien N (t) vorhanden sind, desto mehr werden sie sich auch vermehren;
• in der doppelten (dreifachen, ...) Zeitspanne ist der doppelte (dreifache, ...) Zuwachs an Bakterien festzustellen.

Dies lässt sich auch so ausdrücken, dass das Wachstum der Bakterien der Bakterien proportional zum Bestand N(t) und zur verstrichenen Zeit  ist. Für die Zunahme der Bakterien gilt also:

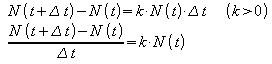
Dieser Differenzenquotient beschreibt die mittlere Wachstumsgeschwindigkeit der Bakterienkultur im Zeitintervall . Der Faktor k wird als Wachstumskonstante bezeichnet.

2. Der Graph von N (t) ist eine „Treppenkurve“. Für kleine Zeitintervalle  und eine große Anzahl von Bakterien ist die Stufenhöhe aber sehr klein. Daher kann der tatsächliche Sachverhalt idealisiert werden, indem die Funktion N (t) als stetig und differenzierbar vorausgesetzt wird. Dann existiert für  der Grenzwert des Differenzenquotienten:

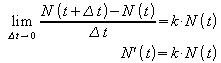
Die Ableitung N'(t) heißt die momentane Wachstumsgeschwindigkeit der Bakterienkultur zum Zeitpunkt t.

Das Gesetz, das hier für die Vermehrung von Bakterien gefunden wurde, lässt sich so formulieren:

3. Dieses Gesetz gilt für viele Wachstumsprozesse. Es wird wie folgt verallgemeinert:

Wird eine zeitlich veränderliche Stoffmenge durch eine differenzierbare Funktion f (t) beschrieben, so heißt das Wachstum exponentielles Wachstum (bzw. exponentieller Zerfall), wenn die momentane Wachstumsgeschwindigkeit (bzw. Zerfallsgeschwindigkeit) f '(t) proportional zu der zum Zeitpunkt t vorhandenen Stoffmenge f (t) ist:

Die Gleichung  heißt auch Diffentialgleichung des exponentiellen Wachstums (bzw. Zerfalls). Um sie zu lösen muss eine Funktion f gefunden werden, deren Ableitung proportional zu der Funktion selbst ist. Die e-Funktion besitzt diese Eigenschaft.

Für t = 0 ist . Die Differentialgleichung des exponentiellen Wachstums wird also durch die Funktion  gelöst.

4. Beispiel 1: Wachstum eines Waldbestands

Der Bestand an fester Holzmasse N(t) wird in Festmetern fm und die Zeit t wird in Jahren gemessen. Das Wachstum verlaufe nach folgender Funktion:

a) Nach welcher Zeit t_D hat sich der Bestand verdoppelt?

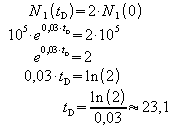
Der Bestand ist also nach etwa 23 Jahren auf die doppelte Größe angewachsen. Dies gilt natürlich nur, wenn keine äußeren Einflüsse vorliegen wie z.B Dezimierung des Bestands durch Abholzen.

b) Graph für t = 0 ... 100:

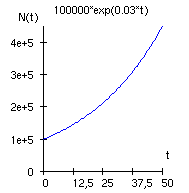
c) Ein anderer Wald habe zur Zeit t = 0 einen Bestand von N₀ = 80 000 fm; seine Wachstumskonstante sei . Wann ist der Holzbestand in beiden Wäldern gleich groß?

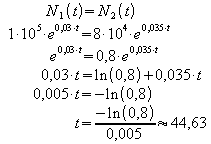
Nach etwa 44,63 Jahren weisen beide Wälder den gleichen Holzbestand auf.

d) Das Integral einer Wachstumsfunktion  führt auf folgenden Zusammenhang:

Es ist also

Dies ist der in der Zeit von 0 bis t erreichte Zuwachs .

5. Vergleicht man in Beispiel 1 den Bestand N₁(t) zu einer Zeit t mit dem Bestand N₁(t + 1) nach einem weiteren Jahr, so ergibt sich immer das Verhältnis

Dieses Verhältnis gibt die prozentuale Vergrößerung des Bestandes in einem Jahr an. Es wird als Wachstumsfaktor a bezeichnet. Damit kann die Wachstumsfunktion in folgender Form geschrieben werden:

Allgemein:

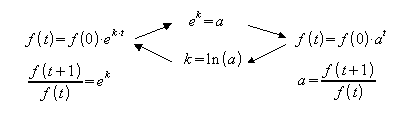
In Fortsetzung des Beispiels 1 wird ein dritter Wald betrachtet, dessen Bestand sich jährlich um 4% vergrößert. Der Wachstumsfaktor ist

die Wachstumsfunktion lautet

Die Wachstumskonstante ergibt sich zu

und die Wachstumsfunktion kann in der Form

geschrieben werden.

6. Beispiel 2: Radioaktiver Zerfall

Die Masse m radioaktiver Stoffe nimmt von einem Anfangswert m(0) = m₀ exponentiell ab: . Für das Radium-Isotop  ist , wenn die Zeit t in Minuten gemessen wird. Wenn anfänglich m₀ = 2 g Radium vorhanden sind, lautet die Zerfallsfunktion also

a) Als Halbwertszeit t_H bezeichnet man die Zeit, nach der nur noch die Hälfte der anfänglichen Masse vorhanden ist - oder anders ausgedrückt: nach der die Hälfte der Anfangsmasse zerfallen ist.

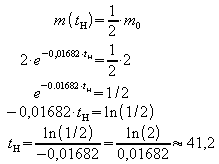
Nach etwa 41,2 Minuten ist also die Hälfte der Radium-Masse zerfallen.

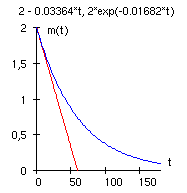
b) Das folgende Diagramm zeigt die Zerfallskurve für die ersten 180 Minuten des Zerfalls.

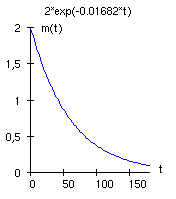
c) Die momentane Zerfallsgeschwindigkeit ist

Zur Zeit t = 0 ist die Zerfallsgeschwindigkeit am größten:

d) Die Gleichung der Tangente an den Graphen von m bei t = 0 lautet:

Sie schneidet die t-Achse an der Stelle t = t_S:
 

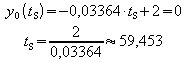Verallgemeinerung der Überlegungen: Es sei

eine Wachstumsfunktion (k > 0) oder eine Zerfallsfunktion (k < 0). Die Gleichung der Tangente an den Graphen von f für t = 0 ergibt sich dann wie folgt:

Ihre Schnittstelle t_S mit der x-Achse ist

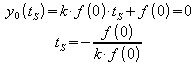also:

e) Das Integral der Zerfallsfunktion  führt auf folgenden Zusammenhang:

Es ist also

Dies ist die in der Zeit von 0 bis t zerfallene Masse .

7. Beispiel 3: exponentielle Abnahme

Auch in klaren Gewässern nimmt die Beleuchtungsstärke B durch das Tageslicht mit zunehmender Tiefe t ab. Bei einem Gewässer sei die Beleuchtungsstärke an der Oberfläche B(0) = B₀ = 4000 Lux. Nach einem Meter, also bei t = 1, beträgt die Beleuchtungsstärke nur noch 80% des Wertes an der Oberfläche. Der Verlauf der Beleuchtungsstärke in Abhängigkeit von der Tiefe soll als exponentielle Abnahme  modelliert werden.

a) Zunächst ist die Abnahmekonstante zu bestimmen.

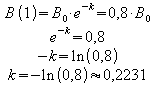
Die Beleuchtungsstärke im Wasser wird also durch die Funktion

beschrieben.

b) In welcher Tiefe ist die Beleuchtungsstärke nur noch halb so groß wie an der Oberfläche?

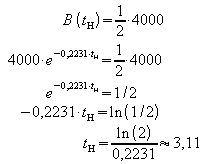
In etwa 3,11 m Tiefe hat sich die Beleuchtungsstärke halbiert.

Probe:.

c) In welcher Tiefe hat die Beleuchtungsstärke gegenüber der Wasseroberfläche um 90% abgenommen?

In dieser Tiefe liegen also nur noch 10% der Beleuchtungsstärke an der Oberfläche vor:

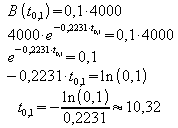
Probe:.

8. Beispiel 4: Bevölkerungswachstum

China und Indien hatten 1988 zusammen etwa  Einwohner. Im Jahr darauf war die Bevölkerung angewachsen auf . Das Bevölkerungswachstum soll als exponentielles Wachstum  modelliert werden.

a) Als Beginn der Beobachtung t = 0 wird das Jahr 1988 gewählt; dann ist .

Wird die Zeit in Jahren gemessen, dann ergibt sich die Wachstumskonstante aus der Bevölkerungszahl im Jahre 1989:

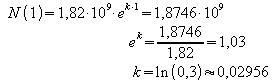
Die Wachstumsfunktion lautet also

b) Wann erreicht in diesem Modell die Bevölkerungszahl die 5-Milliarden-Grenze?

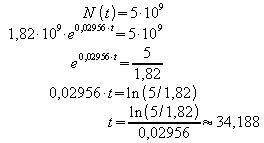
Nach etwa 34,2 Jahren ist die 5-Milliarden-Grenze erreicht.

c) Welche Voraussage machte dieses Modell auf der Basis der Daten von 1988 und 1989 für die Bevölkerungzahl im Jahre 2000?

Da das Jahr 1988 als t = 0 gesetzt wurde, entspricht das Jahr 2000 dem Wert t = 12. Dafür ist

d) Tatsächlich betrug die Bevölkerungszahl im Jahre 2000 aber nur . Welche Gründe kann es für die Abweichung des Modells von der realen Entwicklung geben?

Übungen

1. Zeigen Sie allgemein:
a) Für einen Wachstumsvorgang mit ist die Verdoppelungszeit t_D gegeben durch.

b) Für einen Zerfallsprozess mit  ist die Halbwertszeit t_H gegeben durch .

c) Die Tangente an den Graphen von  für t = 0 schneidet die t-Achse bei .

2. Das Plutonium-Isotop  zerfällt mit der Halbwertszeit t_H = 13,0 Jahre.

a) Stellen Sie die Zerfallsfunktion auf.

b) Wieviel Prozent einer anfänglichen Masse m₀ zerfallen im ersten Jahr?

c) Wieviel Masse ist nach 5 Jahren zerfallen, wenn anfangs 3 mg vorhanden waren?

d) Nach wieviel Jahren sind von einer anfänglichen Masse m₀ 80% zerfallen?

3. Die folgende Tabelle zeigt die Entwicklung der Weltbevölkerung seit 1950:
 

Untersuchen Sie, ob das Wachstum als exponentielles Wachstum modelliert werden kann.

4. In einem Gebiet vermehrt sich ein Heuschreckenschwarm exponentiell, und zwar wöchentlich um 50%. Der Anfangsbestand sei 10 000 Tiere.

a) Geben Sie die Wachstumsfunktion  an.

b) Welcher Zuwachs ist in 6 Wochen zu erwarten?
Um wie viel Prozent hat sich der Bestand dabei vergrößert?

c) Nach welcher Zeit t_D hat sich der Bestand verdoppelt?

5. Zaire hatte 1998 eine Einwohnerzahl von 41 Millionen. Für die folgenden Jahre wurde ein Wachstum von jährlich 3,4% erwartet.

a) Bestimmen Sie die zugehörige Wachstumsfunktion .

b) Welche Einwohnerzahl ergibt sich in diesem Modell für das Jahr 2005 bzw. 2020?

c) Berechnen Sie die Einwohnerzahl vor 2, 5, 10 bzw. 20 Jahren.

6. Der Luftdruck p beträgt in Meereshöhe (Normalnull, NN) etwa 1000 hPa (Hekto-Pascal). Mit zunehmender Höhe h nimmt der Luftdruck exponentiell ab. Bei gleich bleibender Temperatur sinkt der Luftdruck innerhalb von  Aufstieg um 12%.

a) Bestimmen Sie die zugehörige Wachstumsfunktion  (barometrische Höhenformel).

b) Wie groß ist der Luftdruck an folgenden Orten:

• Feldberg im Schwarzwald (1493 m),
• Zugspitze (2963 m),
• Mt.Blanc (4807 m),
• Mt.Everest (8848 m)?