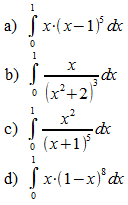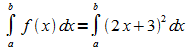
1. Im Integral
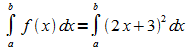
ist der Integrand f eine verkettete Funktion. Die äußere Funktion ist die quadratische Funktion
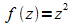 ,
,
die innere Funktion ist die lineare Funktion
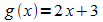 .
.
Bildet man versuchsweise die Funktion
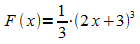 ,
,
so ist nach der Kettenregel
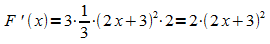 .
.
Dies ist keine Stammfunktion von f, da F '(x) nicht gleich f (x) ist. Es „stört“ die innere Ableitung der linearen Funktion g. Dadurch ist aber leicht zu erkennen, wie man zu einer Stammfunktion von f kommt: F(x) wird durch die Ableitung g'(x) der inneren Funktion g dividiert:
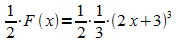 .
.
Nun ist
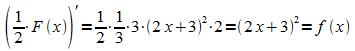 ,
,
und damit ist eine Stammfunktion von f gefunden. Für das Integral ergibt sich somit:
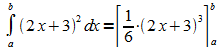 .
.
2. Im folgenden Beispiel ist im Integranden die e-Funktion mit einer linearen Funktion verkettet.
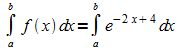
Bildet man hier
 ,
,
so ergibt sich als Ableitung
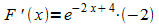 .
.
Daraus ist wieder abzulesen, dass nach Division von F(x) durch die Ableitung der inneren Funktion eine Stammfunktion von f erhalten wird:
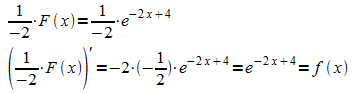
Für das Integral folgt nun:
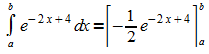
3. Allgemein lässt sich diese Methode so zusammenfassen:
Zu berechnen sei
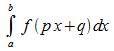 ,
,
wobei
eine auf dem Intervall [a; b] stetige Funktion f
mit der linearen Funktion 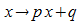 verkettet ist.
verkettet ist.
Wenn F(x) eine Stammfunktion von f (x) ist, dann ist

eine
Stammfunktion von 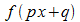 :
:
 .
.
Die Integrationsregel lautet somit:
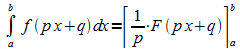
Man bezeichnet diese Integrationsmethode auch als lineare Substitution.
Übungen
Berechnen Sie die folgenden Integrale durch lineare Substitution.
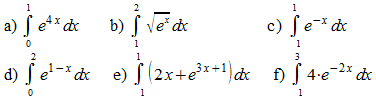
Für
eine Funktion f mit 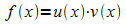 (u und v diferenzierbar) ergibt sich die Ableitung aus
der Produktregel der Differentialrechnung:
(u und v diferenzierbar) ergibt sich die Ableitung aus
der Produktregel der Differentialrechnung:
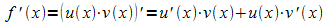
Integration führt auf
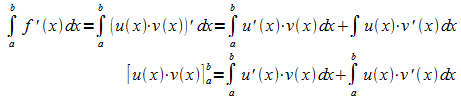
Umgestellt
ergibt sich eine Integrationsregel:
|
Partielle
Integration (Produktintegration): 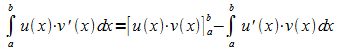 |
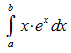
1. Ansatz:

Es
folgt: 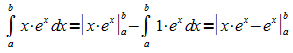
2. Ansatz:
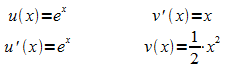
Es
folgt: 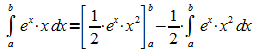
Dieser
Ansatz führt nicht zur Lösung der Aufgabe, macht aber
deutlich, worauf es bei der partiellen Integration ankommt: Die
Faktoren u und v' in 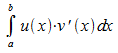 sind so zu wählen, dass das nach Anwenden der Regel für die
partielle Integration verbleibende Integral einfacher wird als das zu
bestimmende Integral.
sind so zu wählen, dass das nach Anwenden der Regel für die
partielle Integration verbleibende Integral einfacher wird als das zu
bestimmende Integral.
Beispiel
2: Zu berechnen ist 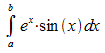
Ansatz:
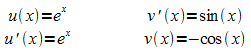
Es
folgt:  (1)
(1)
Das Restintegral wird wieder partiell integriert:
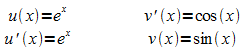
Es
folgt: 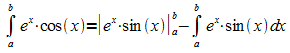 (2)
(2)
Einsetzen von (2) in (1) ergibt:
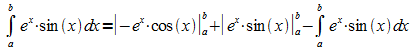
Addition des Integrals auf beiden Seiten:
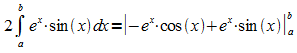
Für das gesuchte Integral folgt daraus:
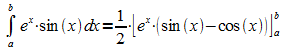
Beispiel
3: Zu berechnen ist 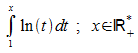
Hier
wird zunächst ein Faktor 1 im Integranden eingefügt: 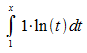
Ansatz:

Es
folgt: 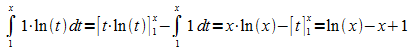
Übungen
1. Berechnen Sie die folgenden Integrale.
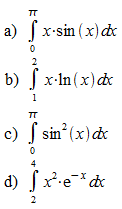
2. Ein
sinusförmiger Wechselstrom wird durch die Gleichung 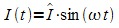 beschrieben.
beschrieben.
Dabei ist 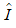 der Scheitelwert,
der Scheitelwert, 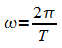 die Kreisfrequenz und T die Periodendauer.
die Kreisfrequenz und T die Periodendauer.
Unter dem
Effektivwert Ieff eines Wechselstroms
versteht man den Wert eines Gleichstroms, der in einem ohmschen
Widerstand R die gleiche mittlere Leistung umsetzt wie der
Wechselstrom. Der Effektivwert ergibt sich aus
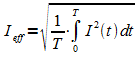
Berechnen
Sie den Effektivwert eines sinusförmigen Wechselstroms.
Als Hilfsmittel soll zunächst der Begriff des Differentials bereit gestellt werden.
Die Ableitung einer Funktion f an einer Stelle x wird bekanntlich in zwei Schritten bestimmt:
1.
Es wird der Differenzenquotient 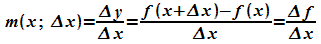 .
Geometrisch
ist dieser als Steigung der Sekante durch zwei Punkte des
Graphen von f zu deuten:
.
Geometrisch
ist dieser als Steigung der Sekante durch zwei Punkte des
Graphen von f zu deuten:

2. Es wird der Grenzwert des Differenzenquotienten gebildet. Wenn der Grenzwert existiert, wird er als Ableitung der Funktion f an der Stelle x bezeichnet.Die geometrische Bedeutung dieser Ableitung ist die Steigung der Tangente an den Graphen der Funktion f an der Stelle x.
Häufig wird eine andere Schreibweise verwendet:
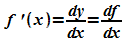
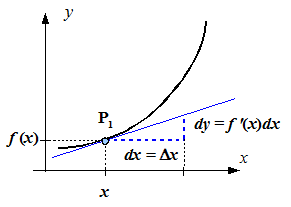
Dabei werden dy (bzw. df) und dx als Differentiale bezeichnet. Die Ableitung wird daher auch Differentialquotient genannt. Die geometrische Bedeutung der Differentiale ist der folgenden Abbildung zu entnehmen: dy ist der Zuwachs der Tangente, wenn x um dx wächst.
Die im Abschnitt 7.1 dargestellte Integration durch lineare Substitution
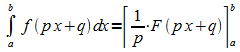
wird durch Multiplikation mit p umgeformt:
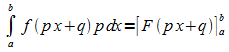
Zur
Abkürzung wird geschrieben 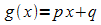 .
Dann gilt
.
Dann gilt 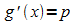 und obige Gleichung geht über in
und obige Gleichung geht über in
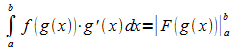
Diese Beziehung gilt auch dann, wenn g keine lineare Funktion ist. Dies lässt sich mit der Kettenregel der Differentialrechnung zeigen.
Vorausgesetzt
wird: f ist eine stetige Funktion und g eine
differenzierbare Funktion mit stetiger Ableitung g'. Dann ist
die Funktion 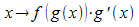 stetig und das Integral
stetig und das Integral 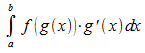 existiert. Weiter sei F eine Stammfunktion von f. Für
die Verkettung
existiert. Weiter sei F eine Stammfunktion von f. Für
die Verkettung 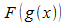 ergibt die Kettenregel:
ergibt die Kettenregel:
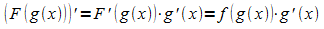
Integriert:
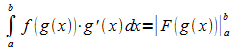
In der praktischen Anwendung dieses Zusammenhangs wird wie folgt vorgegangen:
|
Es ist zu berechnen: |
|
|
Substitution (Ersetzung): |
|
|
Umrechnung der Grenzen: |
|
|
Integration: |
|
Beispiel
1: Zu berechnen ist 
Substitution: 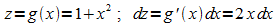
Grenzen: 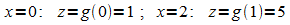
Integration: 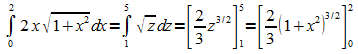
Der letzte Schritt zeigt, dass auf das Umrechnen der Grenzen verzichtet werden kann, wenn die Substitution bei der Auswertung rückgängig gemacht wird.
Beispiel
2: Zu berechnen ist 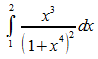
Substitution: 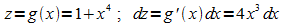
Grenzen: 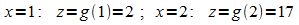
Integration:
Der Integrand muss erst noch umgeformt werden, damit er die Form 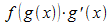 erhält:
erhält:
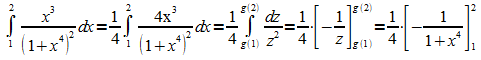
Die Formel für die Integration durch Substitution kann auch von rechts nach links gelesen werden.
|
Es ist zu berechnen: |
|
|
Substitution (Ersetzung): |
wobei g umkehrbar sein muss: |
|
Umrechnung der Grenzen: |
|
|
Integration: |
|
Beispiel:
Zu berechnen ist 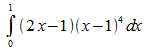
Substitution: 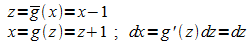
Grenzen: 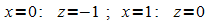
Integration: 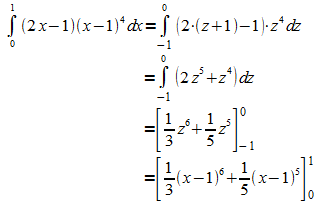
Übungen
1. Bestimmen Sie eine Stammfunktion der Funktion f.
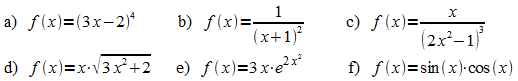
2. Berechnen Sie die folgenden Integrale.